五棱錐SGCMGs失效時奇異構型幾何分析及操縱律設計

王煥杰，劉 禹，張召弟

(1.上海航天控制技術研究所，上海 201109； 2.上海市空間智能控制技術重點實驗室，上海 201109)

0 引言

單框架控制力矩陀螺(SGCMG)作為一種角動量交換裝置，憑借其大力矩輸出特性，在航天器姿態控制領域被廣泛應用[1]。SGCMG在進行三維力矩輸出時，多以3個或3個以上成簇組成一定構型。根據所選SGCMG個數及其安裝方式不同將其分為平行構型和獨立構型。常見的獨立構型有雙平行構型、三平行構型；獨立構型有金字塔構型、五棱錐構型等。文獻[2]介紹了各類構型的分類。文獻[3]分析了SGCMGs構型的幾何特性，并給出了各SGCMGs構型奇異點的理論推導。

基于不同的SGCMGs構型，學者們設計了不同的操縱律，當前操縱律的設計問題主要集中在對雅克比矩陣求逆上。其中最簡單的是偽逆操縱律[4]，此操縱律雖然能得到精確解，但卻無奇異規避能力。帶零運動的偽逆操縱律[5]和魯棒偽逆操縱律[6]是對偽逆操縱律的改進，都在不同程度上實現了對奇異狀態的回避。帶零運動的偽逆操縱律能有效避免構型的內部隱奇異點，但無法解決內部顯奇異問題；魯棒偽逆操縱律在進行奇異規避的同時會引入誤差項，降低控制精度。以上提到的操縱律都是針對某類構型而言，不具備研究的一般化特性。

五棱錐構型由于其內部顯奇異點靠近包絡，已成功應用于“和平號”空間站[7]，但其所采用的帶有零運動的偽逆操縱律具有較強的針對性，對內部奇異復雜的構型并不適用。五棱錐SGCMGs單只失效后，內部奇異點分布情況復雜，具備研究的一般化特性。針對此類奇異點的復雜構型，多采用引入擾動的方法進行奇異規避。文獻[8]采用一種變系數的魯棒偽逆操縱律，文獻[9-10]采用一種引入附加框架加速度的方法，都實現了對奇異的規避，但均未對構型內部的顯奇異點和隱奇異點加以區分。如何在有效規避奇異的基礎上盡量實現指令力矩的精確輸出，是SGCMGs使用研究的重點。從工程應用的角度出發，往往通過引入一定的攝動來保證SGCMGs的有效規避，這就意味著SGCMGs輸出了指令力矩之外的干擾力矩。隨著航天器高精度姿態控制要求的提高，這些干擾力矩需要盡量減小甚至避免。

本文以五棱錐構型為例進行構型分析，對單只陀螺完全失效后構型的內部奇異情況進行了研究，重點對失效前后顯奇異點、隱奇異點的分布進行了分析及量化對比。同時針對單只陀螺失效后，構型具備的一般化奇異特性，綜合零運動規避隱奇異和魯棒偽逆規避顯奇異的優點進行了操縱律設計，在保證奇異規避的基礎上有效減小了干擾力矩。最后，采用單只陀螺失效后的五棱錐SGCMGs構型，以三軸姿態機動任務為例，對所設計的操縱律和傳統的魯棒偽逆操縱律進行了仿真。

1 構型分析

五棱錐構型[11]采用6個SGCMG進行獨立型方式安裝，其中5個被分別安裝在正五棱錐體相鄰的5個側面，另一個沿五棱錐的中軸線方向安裝，任意相鄰兩面的夾角為116.51°。各陀螺的框架軸對稱分布，分別垂直于其所在側面，錐面與地面夾角為β=63.4°。系統構型如圖1所示。

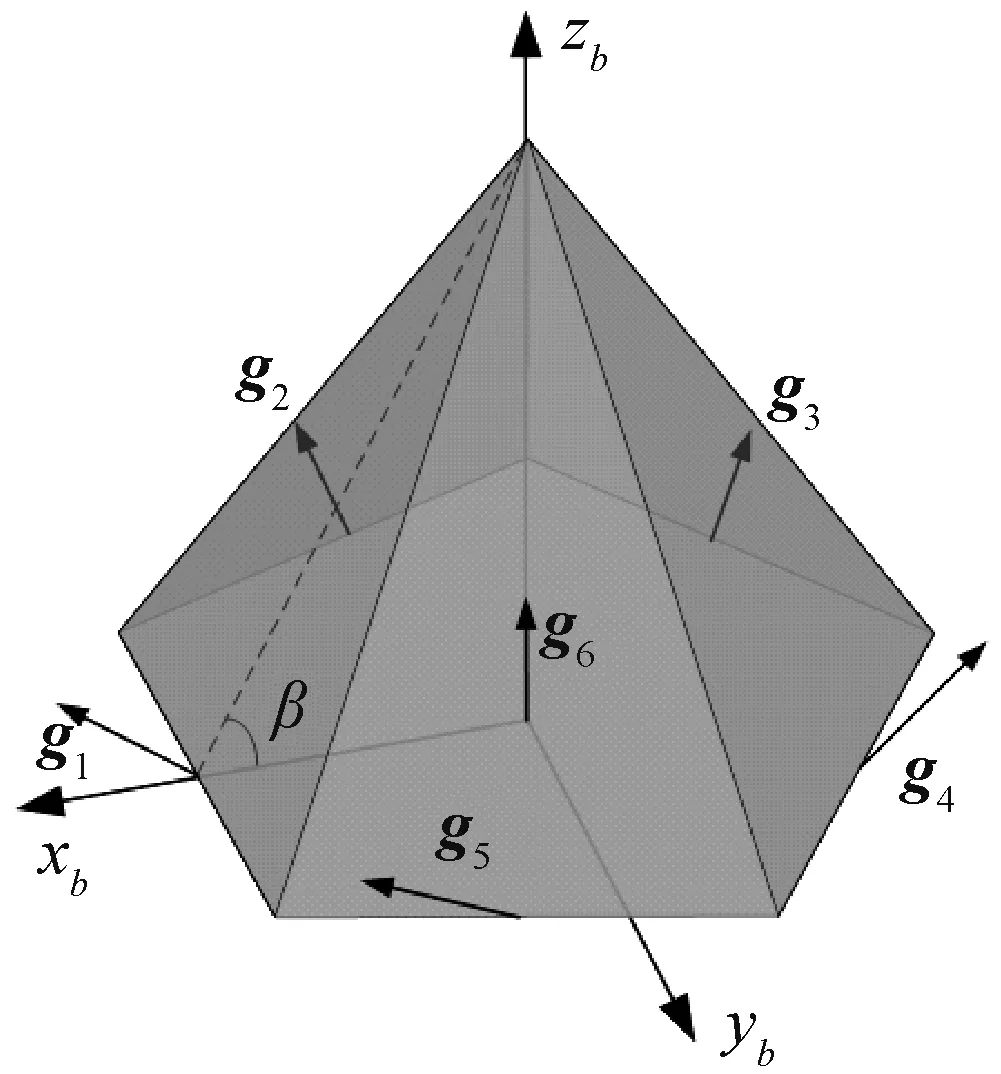
圖1 五棱錐構型示意圖Fig.1 FPC configuration diagram

各框架軸的安裝方向分別為

(1)

根據SGCMG單元的力矩輸出特性，其角動量hi、輸出力矩ci與框架軸安裝方向gi兩兩垂直。在確定框架軸安裝方向后，對應不同的SGCMG框架轉角可求得每個SGCMG的角動量，進而可求得SGCMGs構型的角動量

(2)

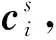
(3)

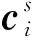
(4)

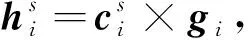
(5)

總的奇異角動量

(6)

由此可得構型的角動量奇異面，如圖2所示。該奇異面包含顯奇異點和隱奇異點，針對每個奇異點，判斷其有無零運動存在[12]。1個奇異點若存在零運動，為隱奇異點，如圖3所示；反之則為顯奇異點，如圖4所示。圖中的Hx、Hy、Hz分別表示角動量在x、y、z軸的分量。

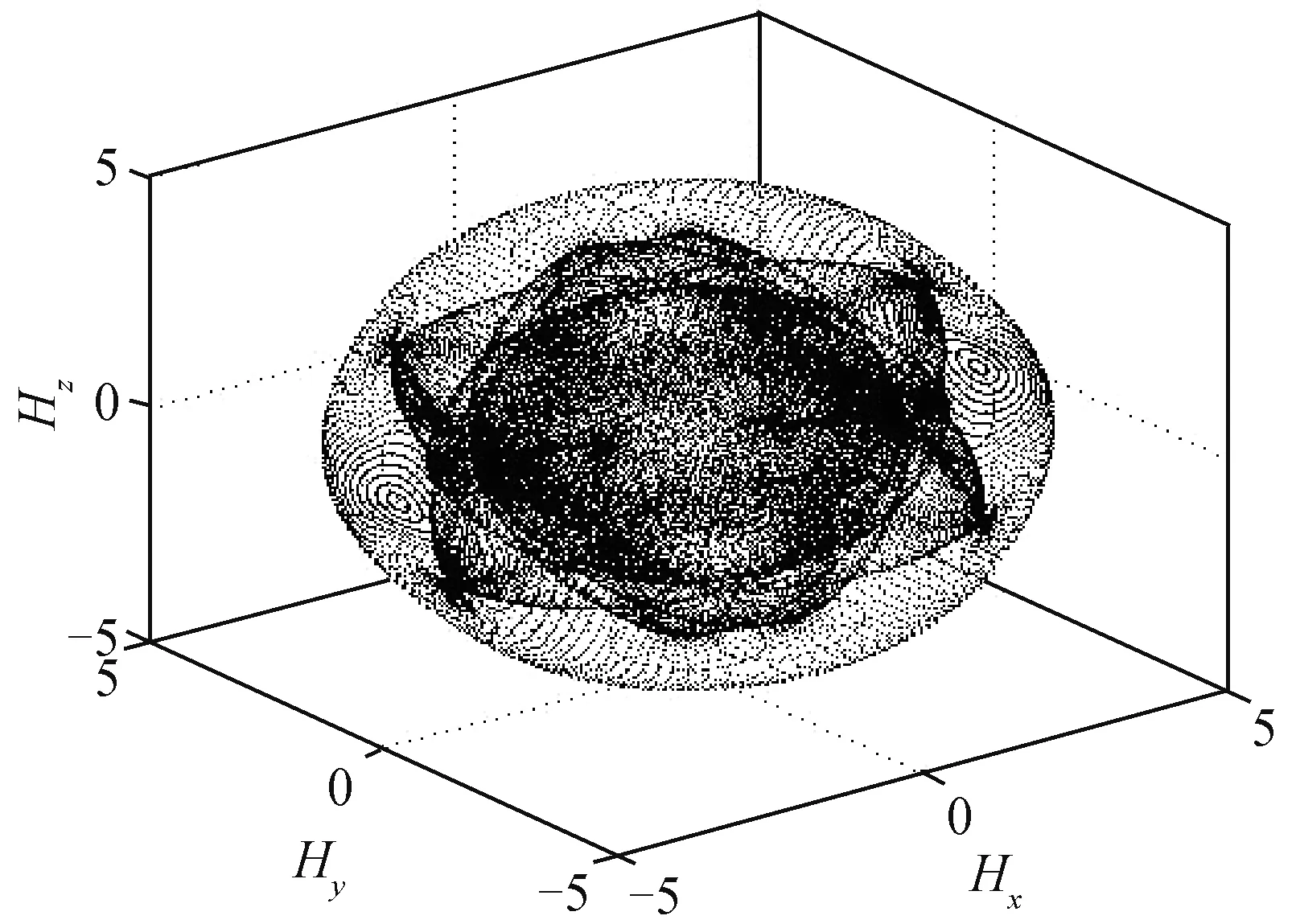
圖2 五棱錐構型奇異面Fig.2 FPC singular surface

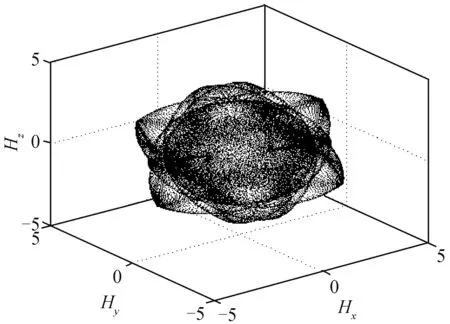
圖3 五棱錐構型隱奇異面Fig.3 FPC passable singular surface

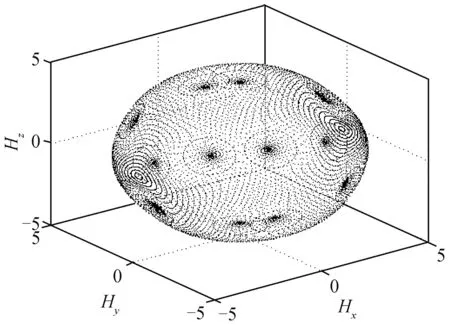
圖4 五棱錐構型顯奇異面Fig.4 FPC impassable singular surface

考慮到五棱錐構型的強對稱性，單只陀螺失效情況以CMG1和CMG6失效為例進行分析，本文只對CMG1失效后構型的奇異面、隱奇異面、顯奇異面進行超曲面輸出，如圖5～7所示。

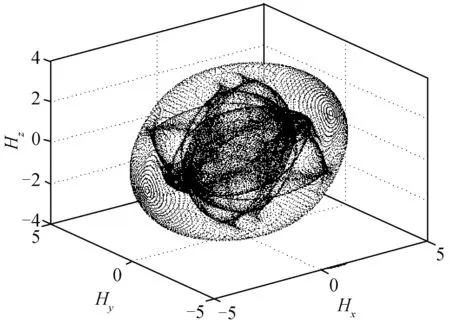
圖5 CMG1失效后奇異面Fig.5 Singular surface after CMG1 is invalid

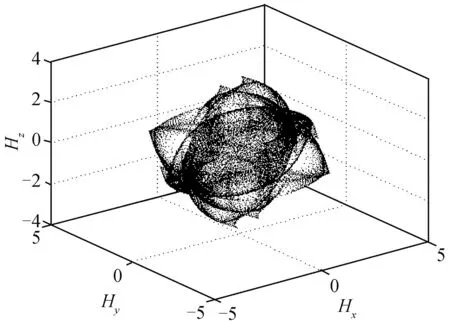
圖6 CMG1失效后隱奇異面Fig.6 Passable singular surface after CMG1 is invalid

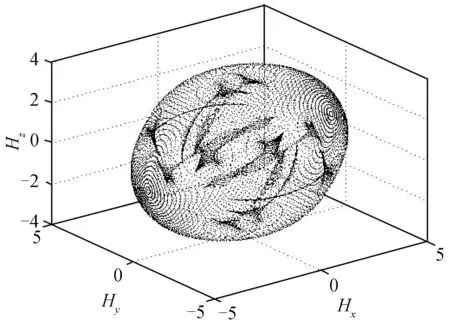
圖7 CMG1失效后顯奇異面Fig.7 Impassable singular surface after CMG1 is invalid

通過比較得到單只陀螺失效前后構型奇異面的幾何特性，見表1。

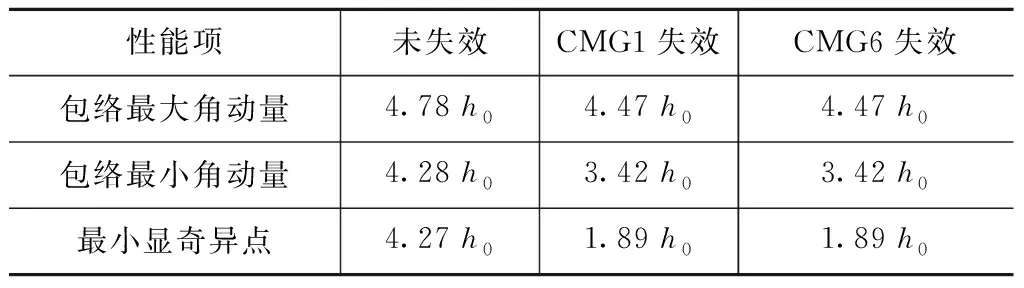
表1 失效前后構型角動量情況

用文獻[13]中的4個性能參數表示構型特性，如下所示：

1) 構型效益。SGCMGs角動量包絡面上的最小值與SGCMGs角動量代數和之比，表征了單個SGCMG對整個構型貢獻的大小。值越大表明單個SGCMG發揮的作用越大。

2) 構型效率。角動量體包絡面上的最小值與最大值之比，值越大表明構型的角動量體越接近球狀，構型在各方向能夠提供的力矩輸出能力越均衡，對工作環境的適應能力也越強。

3) 可控效益。SGCMGs構型最小顯奇異點角動量與SGCMGs角動量的代數和之比。以最小顯奇異點為半徑的開球所表示的角動量體內不會遭遇顯奇異問題，而隱奇異可通過零運動脫離，所以值越大表明系統規避奇異的能力越強，控制能力越強。

4) 奇異點損失率。構型效益與可控效益的差值，值越小表明構型顯奇異點越接近包絡面附近，構型的可控角動量球也就越大。

失效前后構型性能參數匯總見表2。

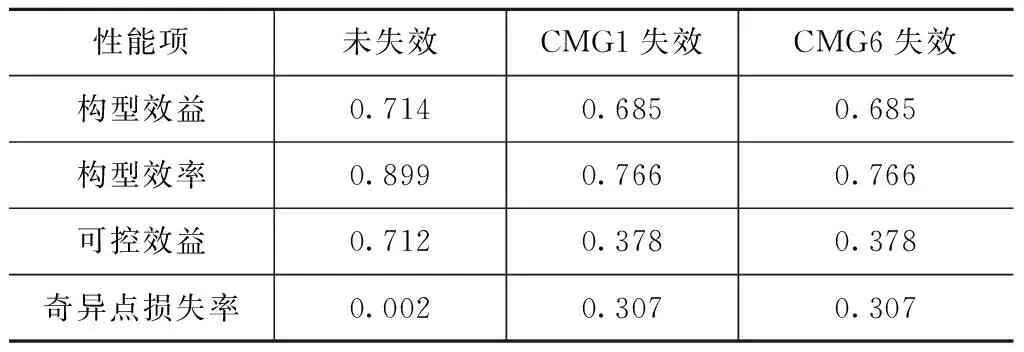
表2 失效前后構型性能參數

通過比較發現，CMG1和CMG6失效后構型變化情況相同，如下所示：

1) 構型角動量體包絡減小，構型效益下降，表明角動量體減小，最大輸出能力下降。

2) 包絡最大角動量與包絡最小角動量相差增大，構型效率下降，表明角動量體偏離球形，構型在三軸方向的力矩輸出能力均衡度變差。

3) 最小顯奇異點遠離包絡，可控效益大幅下降，奇異點損失率大幅上升，表明顯奇異點內切球(球內無顯奇異點)半徑大幅減小，可適用零運動的角動量球縮小。

2 操縱律設

五棱錐構型中，半徑為4.27h0的角動量球內只有隱奇異點存在。針對隱奇異點可通過零運動規避的特性，文獻[11]采用“偽逆+零運動”操縱律，這一操縱律對此類顯奇異點內切球較大的構型具有明顯的適用性，具體描述如下：

(7)

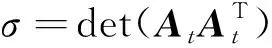
單只陀螺失效后帶來的最明顯變化是五棱錐構型內部奇異點組成的復雜化，失效后該半徑迅速下降至1.889h0。若仍舊采用“偽逆+零運動”操縱律，則將工作空間限制在該內切球內，一旦超出該球范圍極有可能遭遇顯奇異點，而“偽逆+零運動”顯然不具備規避顯奇異點的能力。對于這類顯奇異點深入角動量體內部的構型，文獻[6]設計了攝動魯棒偽逆操縱律，如下所示：

(8)

式中：λ為正誤差項系數；I3×3為單位陣；E3×3為攝動矩陣,其中

(9)

式中：εj為適當選取的小量，εj=0.01sin(0.5πt+φj)(j=1，2，3)。相位差分別為φ1=0，φ2=0.5π，φ3=π。

該操縱律通過引入誤差攝動項進行奇異規避，對顯、隱奇異點均適用，但由于引入誤差項會帶來額外的誤差力矩輸出，不利于高精度的姿態控制。

基于以上2種操縱律的優缺點，本文設計了一種帶零運動的魯棒偽逆操縱律。設計的基本思路為：在角動量向奇異點逼近的過程中，優先將此奇異點作為隱奇異點處理，引入零運動進行規避，若奇異狀態未惡化至閾值狀態(σ≥σ1)時，仍將此點作為隱奇異點處理；當奇異情況進一步惡化，奇異值低于閾值(σ<σ1)時，表明零運動效果不佳，此時將奇異點作為顯奇異點處理，引入攝動項進行規避。具體形式為

(10)

系數λ，α選取規則為

(11)

當構型大于奇異度量閾值σ1時，優先對內部隱奇異點進行規避，此時求解準確，不引入誤差項；當構型奇異度量小于σ1時，表明零運動作用不大，此時引入攝動項，為避免指令框架角速度過大，將零運動項置零。這樣能在充分利用內部隱奇異點的基礎上實現對顯奇異點的規避。選取閾值σ1時不宜過大，閾值越大表明零運動作用的區間越小，攝動工作區間越大。閾值選取原則為：在盡量擴大零運動作用區間的同時，保證攝動能及時規避顯奇異點。

3 平臺動力學建模

為驗證操縱律的控制效果，建立以SGCMGs為執行機構的衛星姿態動力學模型，有

(12)

式中：J為包含SGCMGs在內的整星慣量陣，J=Jb+JCMG；h為SGCMGs構型角動量；ω為衛星本體相對慣性系的角速度；Tc為SGCMGs輸出力矩；Te為外部力矩[14]。

采用四元數描述衛星的運動學方程，有

(13)

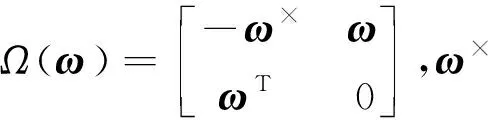
4 仿真分析

設飛行器相對質心坐標系的慣量為

Jb=diag(4 000 3 000 3 000)kg·m2

單個SGCMG的角動量h0=25 N·m·s，最大力矩輸出為10 N·m。衛星初始三軸慣性姿態角均為1°，三軸角速度均為0.1 (°)/s，三軸外部干擾力矩為1 mN·m。采用5次多項式法設計一種三軸姿態機動標準軌跡，軌跡時長80 s，機動角度0°。噴氣卸載觸發條件為

(14)

以CMG1失效為例，分別采用魯棒偽逆操縱律和帶零運動的魯棒偽逆操縱律進行仿真。

圖8～10分別為三軸跟蹤標準軌跡進行姿態機動的姿態角曲線，可以發現在40 s左右采用魯棒偽逆操縱律得到的三軸機動曲線明顯偏離標準軌跡，偏差為2°以上。結合圖11可知，這是由于噴氣卸載干擾造成的，卸載結束后，曲線逐漸收斂。而采用帶有零運動的魯棒偽逆操縱律機動效果明顯優于前者，實時跟蹤精度能達到0.01°以上。

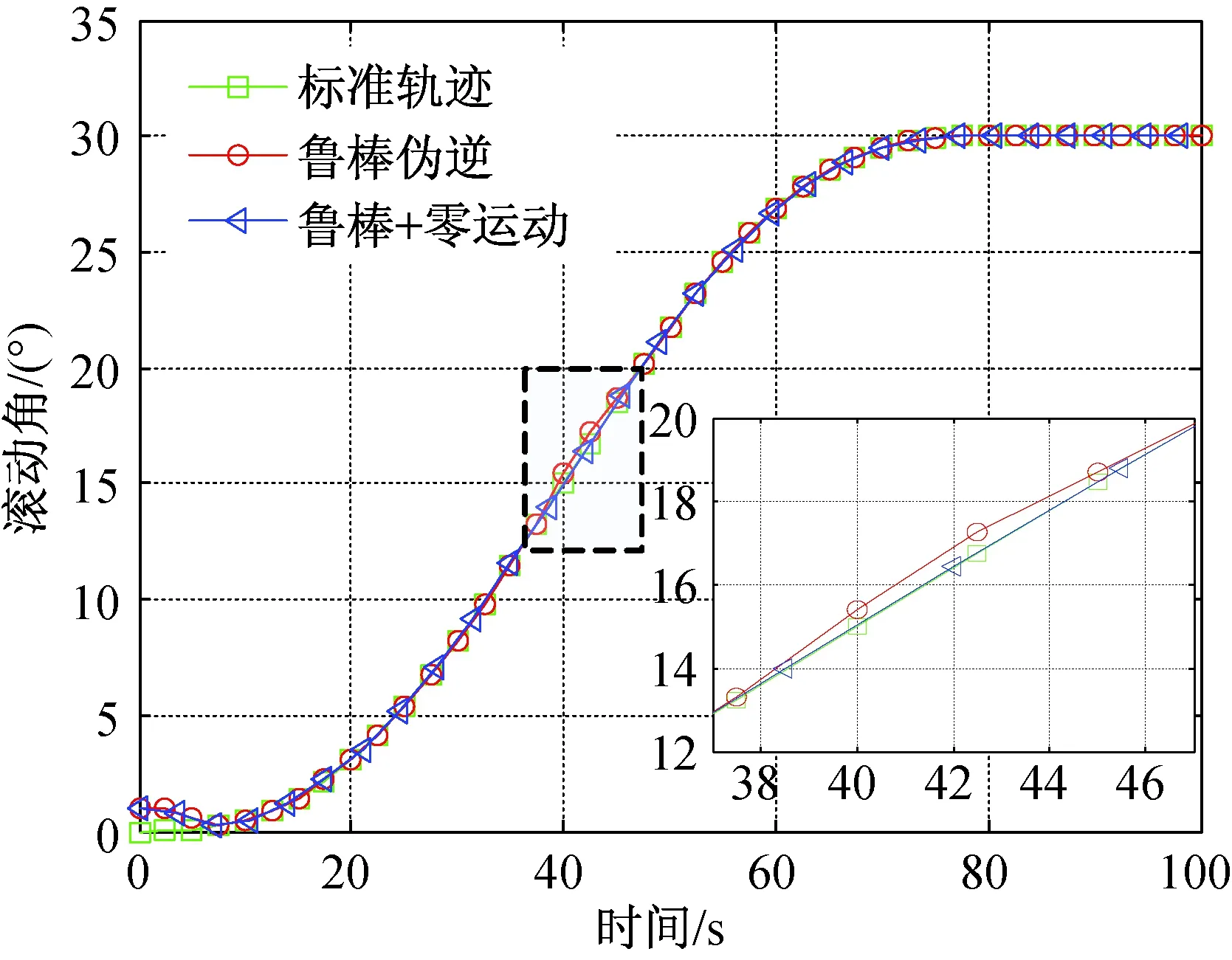
圖8 滾動角機動曲線Fig.8 Roll angle maneuvering trajectory

圖9 俯仰角機動曲線Fig.9 Pitch angle maneuvering trajectory

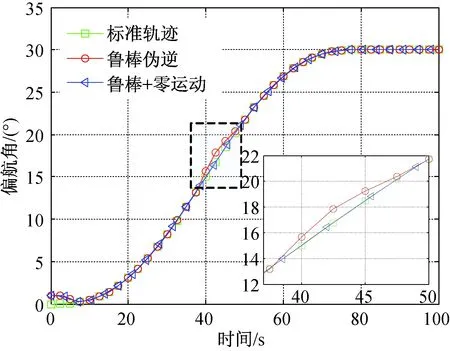
圖10 偏航角機動曲線Fig.10 Yaw angle maneuvering trajectory

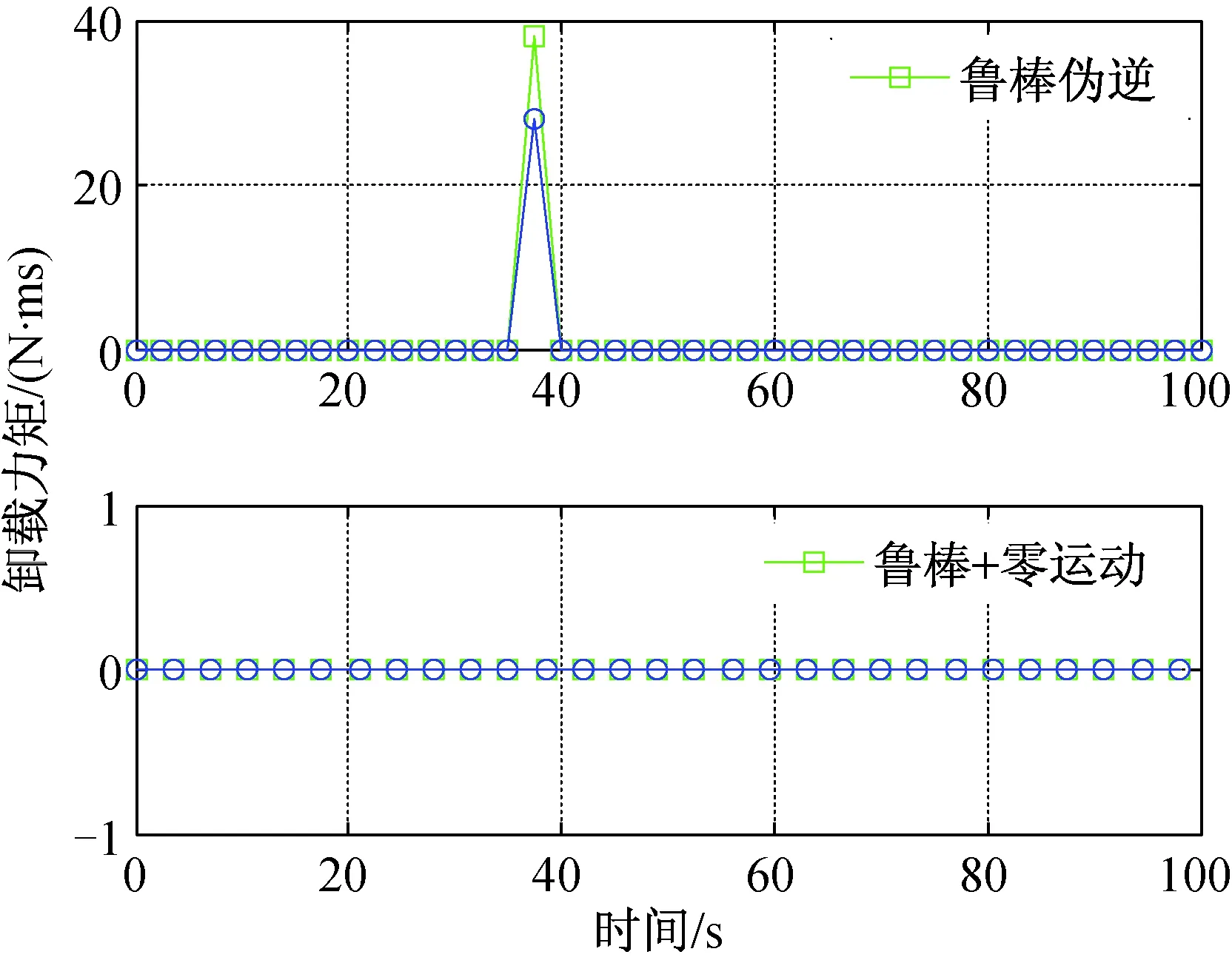
圖11 噴氣卸載力矩Fig.11 Jet unloading torque

結合噴氣卸載力矩、構型角動量及構型奇異度量，可以得出：采用魯棒偽逆操縱律在機動過程中雖然避免了內部的奇異狀況，但由于攝動的影響造成額外的力矩輸出，在40 s前后角動量約為80 N·m·s，且奇異度量在接近0.2時觸發噴氣卸載，造成跟蹤誤差增大。而采用帶有零運動的魯棒偽逆操縱律充分利用了角動量體內部的隱奇異點，奇異度量始終保持在0.5以上，表明構型始終遠離奇異狀態。

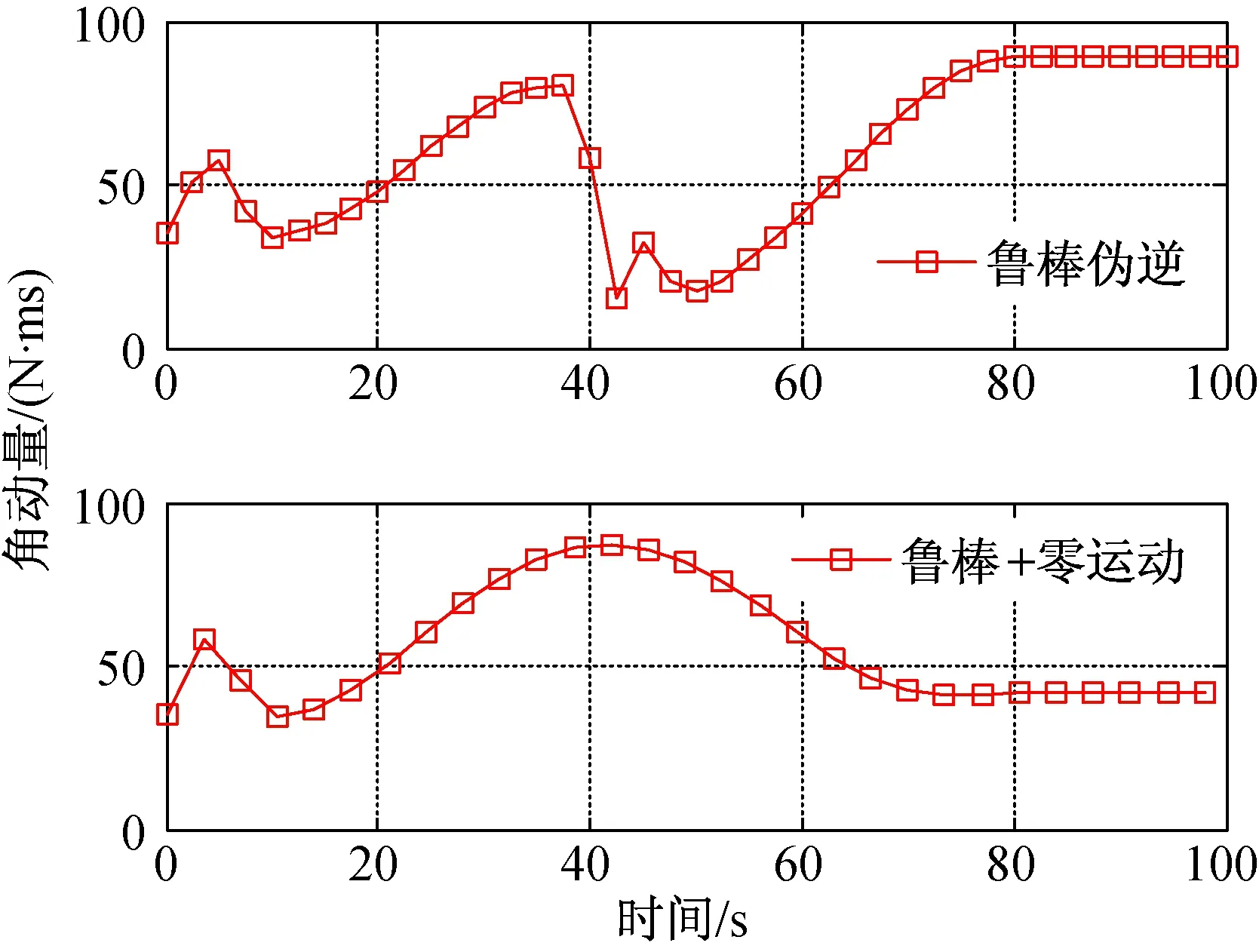
圖12 構型角動量曲線Fig.12 Configuration angular momentum curve

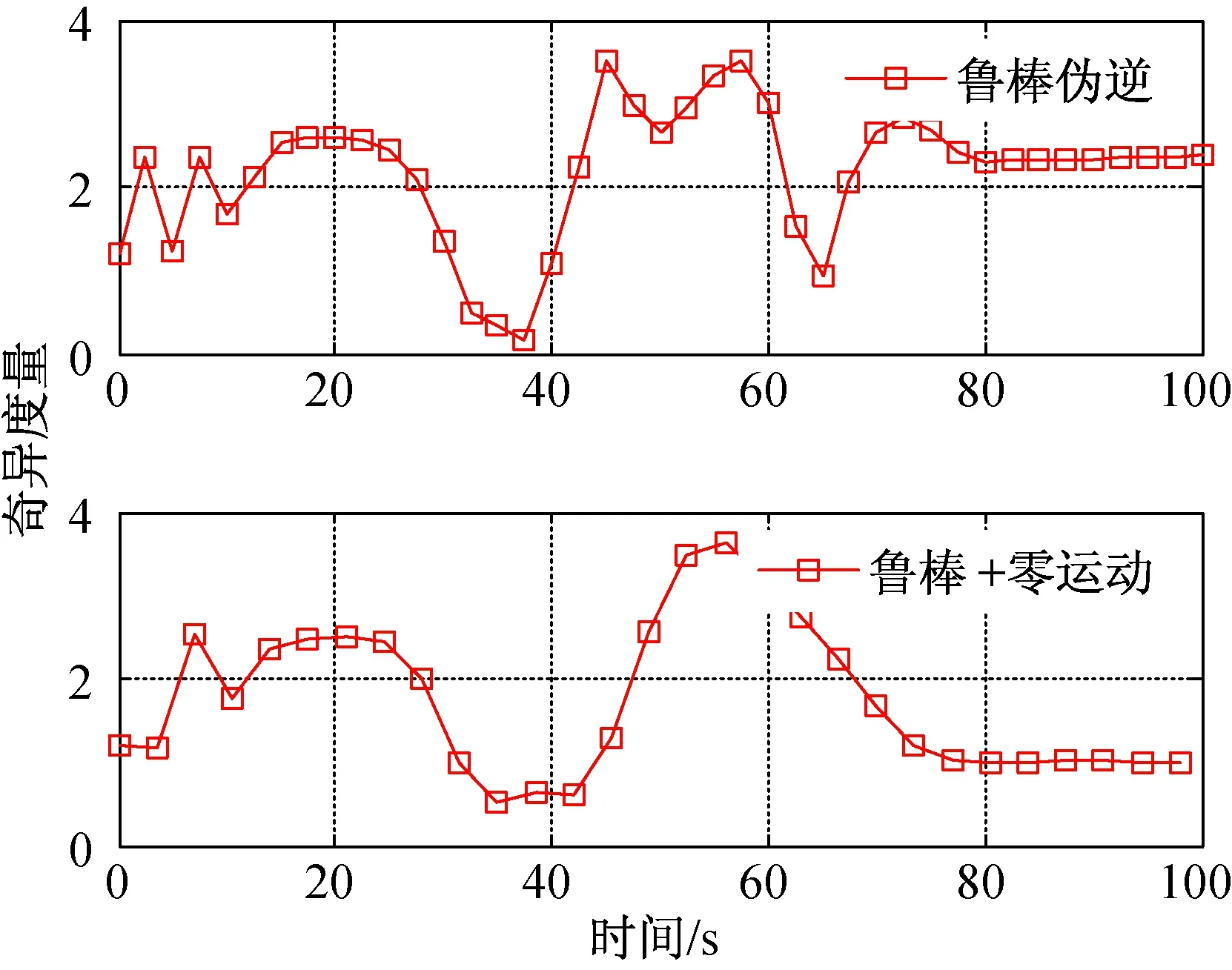
圖13 構型奇異度量曲線Fig.13 Singularity index curve

5 結束語

本文針對五棱錐SGCMGs構型及單只陀螺失效情況下的內部奇異狀況進行了幾何分析，并計算得到了一系列的性能參數。基于單只陀螺失效后內部奇異的復雜情況，在前人研究的基礎上設計了一種適用于顯奇異點深入角動量體SGCMGs構型的綜合操縱律，在規避顯奇異點的基礎上充分利用內部的隱奇異點。通過仿真比較發現，本文設計的綜合操縱律控制效果優于傳統的魯棒偽逆操縱律。該設計的操縱律結合了魯棒偽逆和帶零運動的偽逆操縱律的優點，對于內部顯奇異點進行攝動規避，隱奇異點進行零運動規避，在規避奇異方面具有一定通用性，同樣適用于金字塔型、雙平型等多種SGCMGs構型，在工程上具有一定的實用性。

本文通過閾值的選取將角動量工作空間劃分兩部分(σ<σ1和σ≥σ1)，未考慮兩者間的過渡區域。后續可在考慮SGCMG最大框架角速度的前提下，增加σ1的過渡部分，通過優化參數配置實現零運動的偽逆操縱律向魯棒偽逆操縱律的小擾動過渡。