子空間跟蹤算法在熱模態問題中的應用研究

周昊天，趙 婕，曹為政，史曉鳴，于開平

(1.哈爾濱工業大學 航天學院，黑龍江 哈爾濱 150001； 2.黑龍江科技大學 計算機與信息工程學院，黑龍江 哈爾濱 150022； 3.上海機電工程研究所，上海 201109)

0 引言

近年來，高超聲速飛行器因其在速度上的巨大優勢而受到研究和應用領域的廣泛關注[1]，以高超聲速飛行器為背景的研究成為各領域的研究熱點。高超聲速飛行器的高速特性也給各領域的研究帶來了諸多挑戰[2]。如何辨識在氣動加熱環境下結構的模態參數是結構動力學領域遇到的挑戰之一。處于飛行狀態的飛行器模態參數的辨識問題一直備受關注[3]，因無法獲知其所受外載荷的詳細信息，故一般采用運行模態分析(OMA)方法。此外，由于飛行器的熱環境隨飛行狀態的改變而改變[4]，結構的動力學特性也隨時間的變化而變化，因而需要用時變模態參數辨識方法解決這一問題。

子空間跟蹤方法是眾多時變模態參數辨識方法中常用的一類方法。文獻[5]提出了基于快速近似子空間跟蹤(FAST)的時變模態參數辨識方法，對一三連桿系統進行了辨識；文獻[6-7]引入了投影估計子空間跟蹤(PAST)算法，對二連桿和移動質量-簡支梁進行了辨識；文獻[8]引入了自然冪迭代(NPI)和估計冪迭代(API)方法，對彈簧-質量兩自由度系統和移動質量-懸臂梁系統進行了辨識；文獻[9-10]利用改進的API方法對一二連桿機構和一個衛星模型進行了辨識；此外，還有基于新信息準則(NIC)的子空間跟蹤算法[11]。近年來，也有一些學者進行了熱環境下飛行器動力學特性的試驗研究。余艷輝等[12]研究了金屬熱防護結構在熱載荷作用下的動力學特性；蘇華昌等[13]提出了改進的熱模態試驗方法，利用振動臺對試件施加猝發快掃形式的基礎激勵，并結合激光測振儀進行非接觸式測量，最終獲得舵面一階頻率隨時間和溫度的變化規律；楊凱等[14]設計了一套溫度可控的實驗設備，采用時頻分析方法對時變結構進行了辨識；李宇峰等[15]研究了氣動加熱的模擬方法，獲得了不同溫度梯度條件下熱防護壁板結構的振型、固有頻率等模態信息。

傳統的熱模態分析采用頻域方法，在某一短時間段內將結構視為時不變系統，并在此時間段內進行辨識，無法形成完整連續的辨識結果。針對此問題，本文總結了子空間跟蹤辨識模態參數的一般步驟，利用一個時變兩自由度系統模型的響應數據，通過添加不同量級噪聲來對系統進行再辨識，考察了3種應用較為廣泛的子空間跟蹤算法和1種較新的基于新信息準則的子空間跟蹤算法，并從中選出了抗噪能力最強的算法。最后，設計了飛行器舵面結構的加熱試驗，利用優選出的子空間跟蹤算法對結構升溫階段的模態參數進行了辨識，得出了結構完整的連續時間固有頻率變化規律。

1 方法過程簡介

考慮離散時變狀態方程

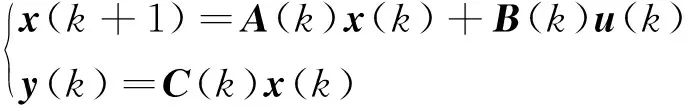
(1)

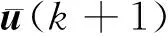
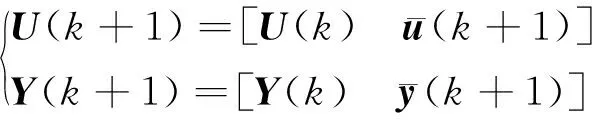
(2)

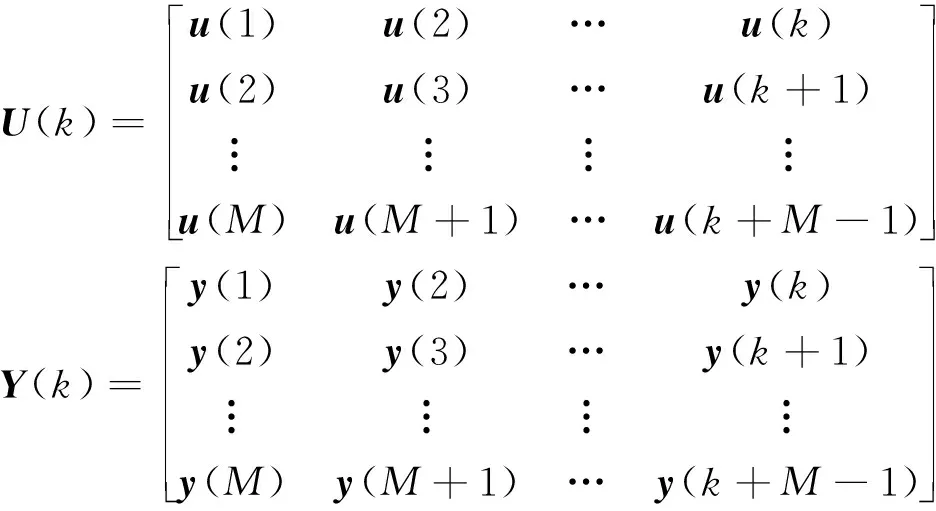
式中：k為時刻；M為選定的Hankel矩陣塊行數。

由此得到狀態量z(k)的更新方式為

(3)

式中：上標“?”表示求對應矩陣的偽逆。且

(4)

(5)

式(3)、(4)中Y(k)U?(k)和[U(k)UT(k)]-1的更新方式為

[Y(k)U?(k)]=[Y(k-1)U?(k-1)]-

z(k)wT(k)

(6)

[U(k)UT(k)]-1=[U(k-1)UT(k-1)]-1-

(7)

式(3)～(7)組成了狀態量z(k)的更新規則。對任意k時刻的輸入矩陣U(k)組建其對應的投影矩陣U⊥(k)，使得U(k)U⊥(k)=0，則有

U⊥(k)=I-U?(k)U(k)=

I-UT(k)[U(k)UT(k)]-1U(k)

(8)

且

Y(k)U⊥(k)=

Y(k)-Y(k)UT(k)(U(k)UT(k))-1U(k)=

Γ(k)X(k)U⊥(k)

(9)

對Y(k)U⊥(k)進行奇異值分解(SVD)，可得

Y(k)U⊥(k)=R(k)Σ(k)V(k)T

(10)

式中：由R(k)的前n列組成的矩陣即為k時刻的廣義能觀矩陣Γ(k)。

tr(WT(k)W(k))

(11)

式中：Rzz(k)=E[z(k)zT(k)]。此處：“E”表示期望；“tr”表示矩陣的跡。子空間跟蹤方法優化問題具體求解過程可參考文獻[5-10]。

得到任一k時刻的信號子空間后，可通過式(12)估計離散系統矩陣，具體為

(12)

式中：W1(k)和W2(k)分別由W(k)的前(M-1)×m和后(M-1)×m行組成。對估得的離散系統矩陣進行特征值分解，可得

(13)

式中：Λ(k)=diag(λ1(k),λ2(k),…,λn(k))表示由共軛復特征值組成的對角陣；ψ(k)為特征向量。k時刻第i階系統偽固有頻率ωi(k)和模態阻尼比ξi(k)可通過式(14)、(15)求得，即

ωi(k)=ln(λi(k))/(2Δtπ)

(14)

(15)

式中：上標“R”表示實部；Δt為數據采樣周期。

綜上所述，基于子空間跟蹤的時變模態參數辨識方法的一般步驟可總結如下：

1)對激勵和響應數據進行預處理，使數據滿足遞推步驟的需要，得到狀態向量z(k)；

3)利用復模態分析理論得出時變頻率ωi(k)、時變模態阻尼比ξi(k)等模態參數；

4)重復步驟1)～3)，直至所有響應數據被處理。

2 仿真計算

本節對一個有理論參考解的兩自由度彈簧-質量系統進行辨識，系統簡圖如圖1所示。

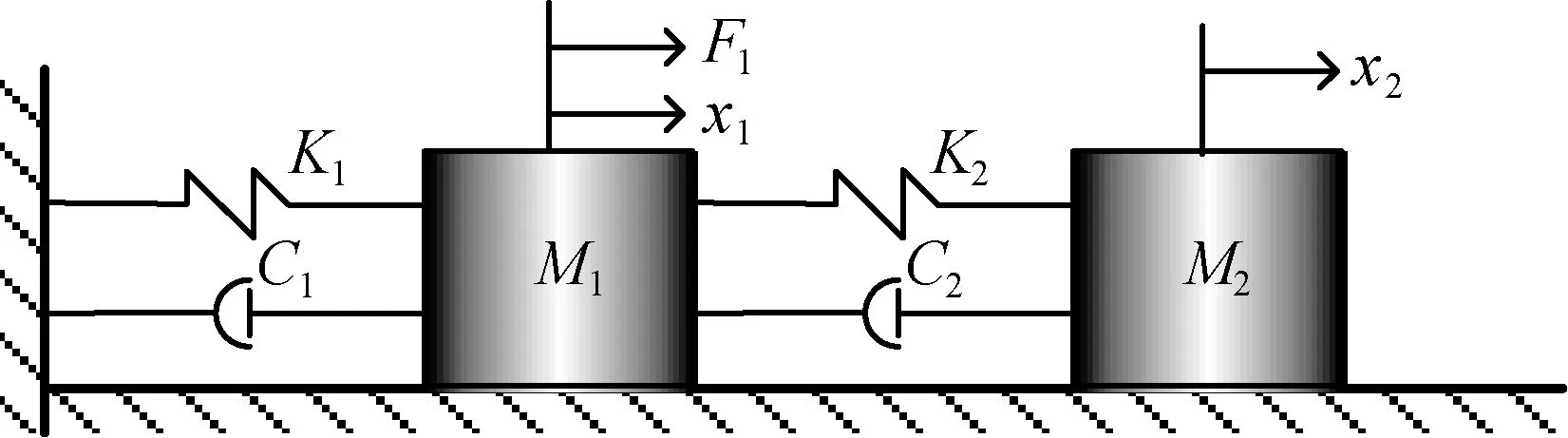
圖1 兩自由度彈簧-質量模型示意圖Fig.1 Schematic diagram of two degree-of-freedom spring-mass model

系統的運動控制方程為

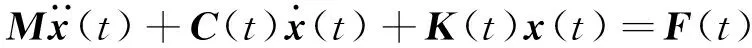
(16)

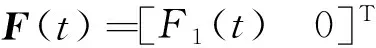
(17)

系統剛度矩陣K(t)取值為

(18)

系統阻尼矩陣C(t)為

0.5M+10-4K(t)

(19)

為模擬舵面受熱時的剛度變化情況，令式(18)中剛度K1(t)=1 000 exp(-0.4t)，K2=2 000，仿真計算的時間步長Δt=1 ms，時長總計為5 s。辨識方法采用文獻[2-7]中所述方法。為模擬實測結構響應，在仿真響應數據中添加一定量的噪聲，使最終的響應數據信噪比(SNR)為10。各方法采用相同的計算參數，最終辨識結果如圖2所示。

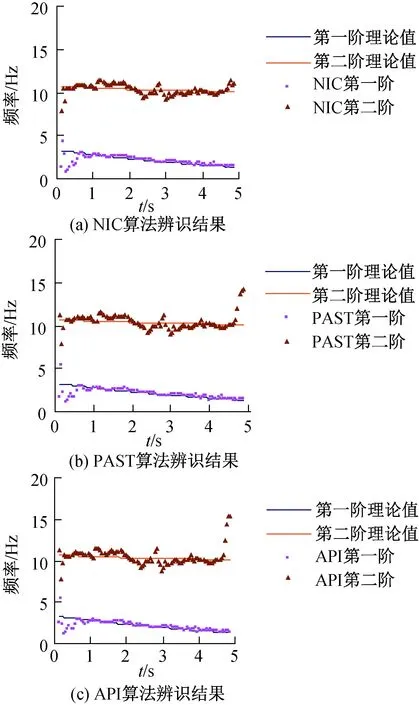
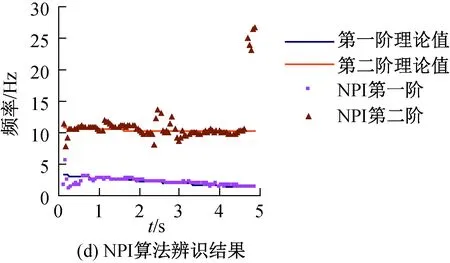
圖2 信噪比為10時各算法辨識結果Fig.2 Identification results with differentalgorithms when SNR equals to 10

圖中：低于5 Hz的頻率為第一階固有頻率；10 Hz左右的頻率為第二階固有頻率；實線部分為仿真模型的理論參考值；點線部分為各算法辨識值。從圖中可以看出，各算法都能很好地辨識出兩階固有頻率，且能對固有頻率進行跟蹤。其中：NPI算法的第二階辨識結果在某些時刻偏離理論參考值較遠；API算法和PAST算法的辨識結果非常接近；NIC算法的辨識結果更為接近理論參考值，總體上看精度更高。

為對不同算法在不同量級噪聲情況下的辨識結果進行量化評估，引入平均絕對誤差率(MAPE)，其定義為

(20)

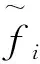
通過以上4種算法并利用信噪比分別為25，15，5，2時的響應數據進行辨識，最終得到的辨識結果MAPE值如表1所示。

表1 不同算法辨識結果MAPE值比較

從表1中可以看出：在響應信號質量較好時，各算法均能很好地辨識結果，各階次相對理論參考值的誤差較小；隨著信噪比的降低，各算法辨識結果的誤差隨之增大，本例中，NPI算法和API算法在信噪比為5時的第二階辨識結果MAPE值超過了50%，說明辨識結果已不可信。從辨識結果的精度來看，在諸多算法中，PAST算法和NIC算法表現較好，在信號質量較差時也能對結構的固有頻率做出估計。在信噪比為5時，各算法辨識結果如圖3所示。

由圖可知：NPI算法辨識結果的第二階誤差較大，在2～3 s時間段內失去了頻率跟蹤能力；從總體上看，相較于其他幾種算法，NIC算法的辨識結果更接近理論參考值，可認為NIC算法的抗噪聲能力更強。

3 飛行器典型結構熱模態辨識

飛行器中存在大量的梁、板類結構，如飛行器舵面。在飛行器飛行過程中，舵面結構所在的熱力學環境也會隨之變化，由此導致的結構動力學特性的變化一直是工業領域的關注熱點。因此，本節對一個鈦合金舵面結構進行辨識，該舵面結構的三維尺寸如圖4所示。

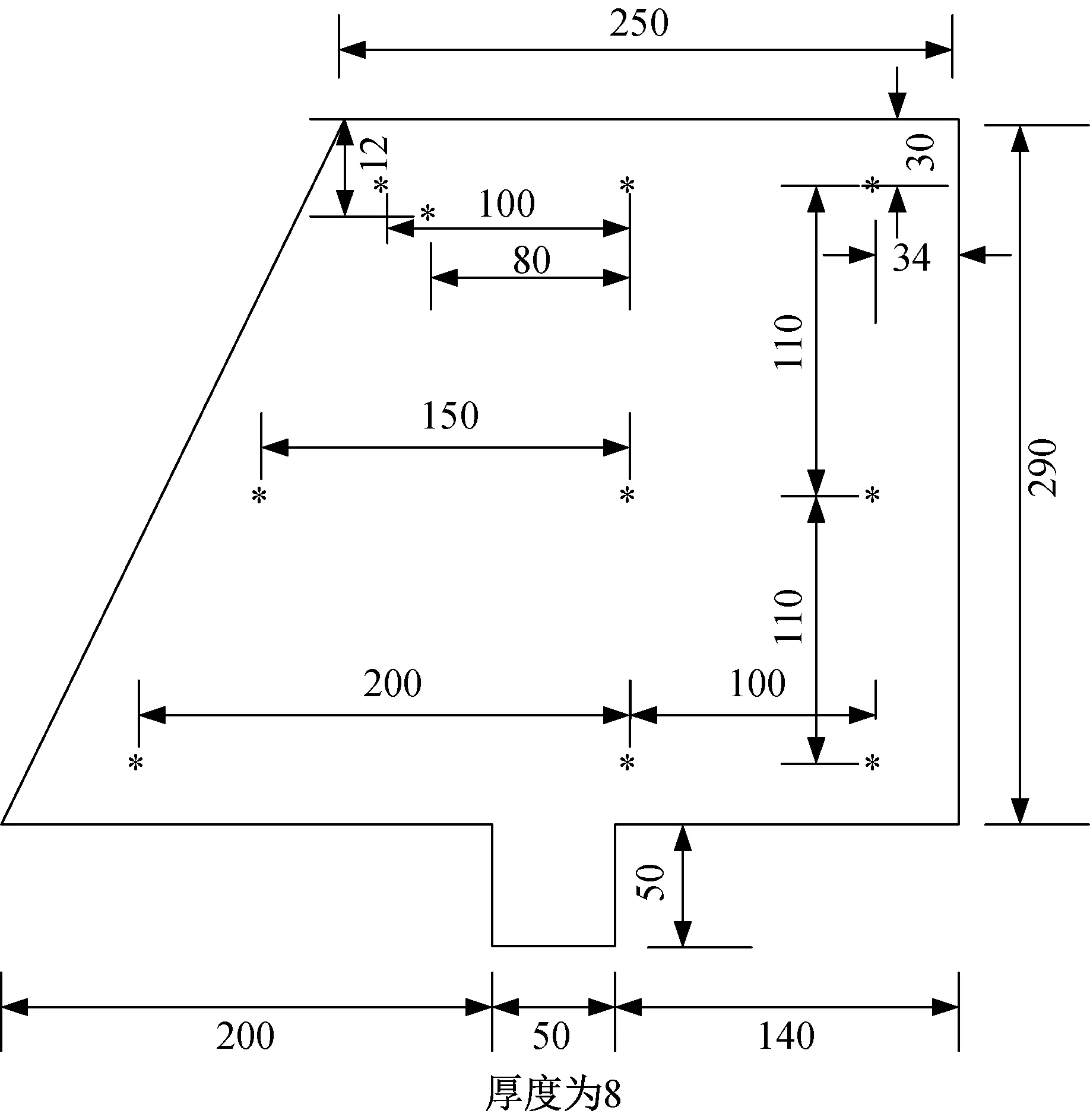
圖4 舵面結構尺寸以及傳感器布置圖(mm)Fig.4 Profile of rudder structure and sensor distribution(mm)

舵面結構為鈦合金TA15材質，舵面根部突出部分用于夾持實驗夾具。圖中：“*”號標記處為高溫傳感器布置點，其中，舵面左上方第二個位置處為激勵點，其余為加速度響應測量點。

高溫實驗裝置原理如圖5所示。圖中：(1)為與試驗件相匹配的夾具；(2)為水冷組件；(3)為紅外石英燈陣；(4)為試驗件；(5)為高溫加速度傳感器；(6)為測溫熱電偶；(7)為激振桿；(8)為力傳感器；(9)為激振器。數據采集系統集成了信號發生器的功能。激振器通過功率放大器與數據采集器相連，其余傳感器通過電荷放大器與數據采集器相連。溫控PLC內置了溫控程序，結合測溫熱電偶按照設定好的溫度曲線對石英燈陣進行功率控制，從而實現控制試驗件溫度的功能。

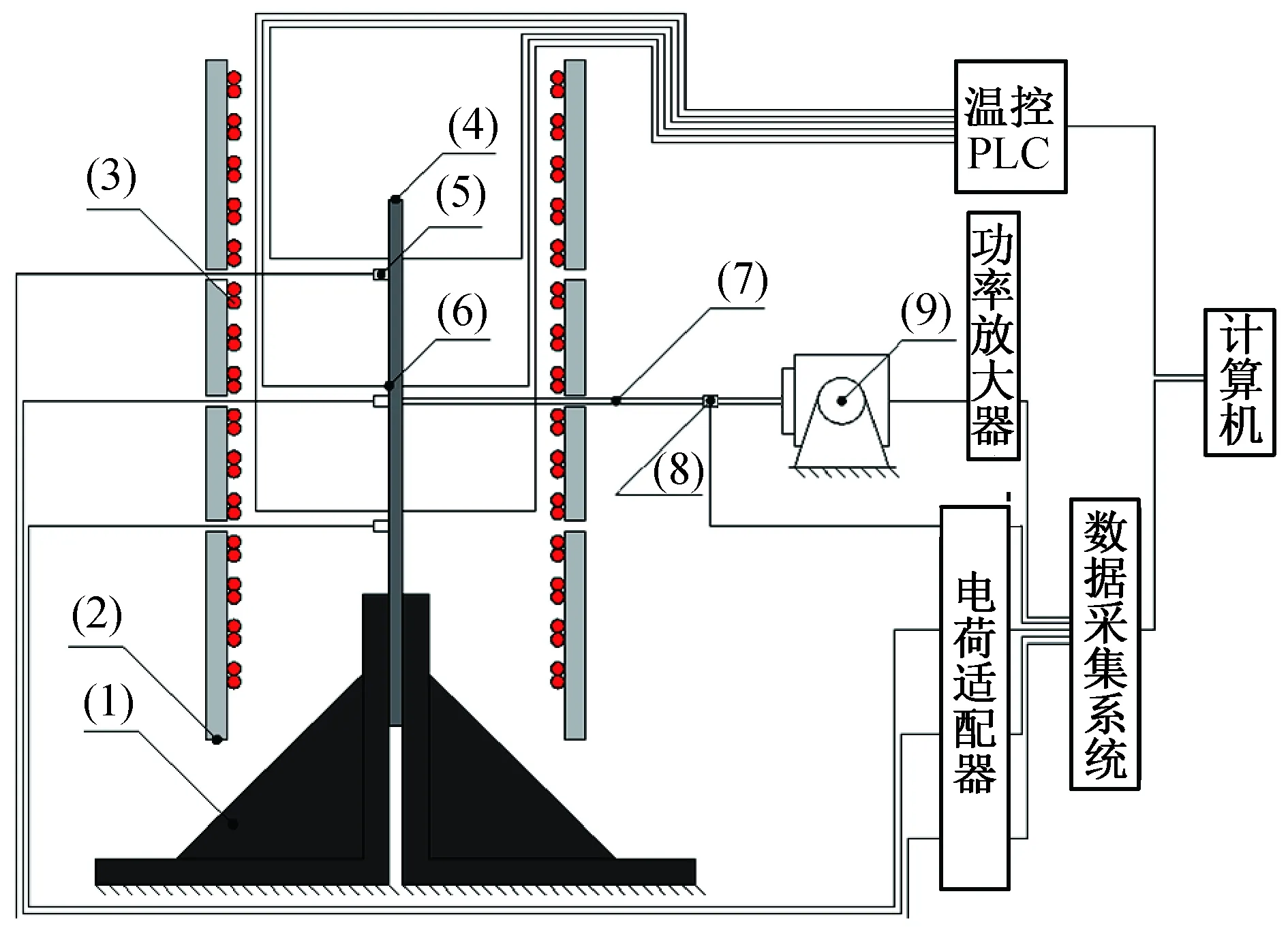
圖5 實驗裝置原理圖Fig.5 Schematic diagram of experiment setup

實驗過程中對試件施加均方根值為1 N的白噪聲激勵。未進行加熱前首先采集30 s的結構振動響應數據；而后通過石英燈陣加熱使舵面溫度在24 s內由常溫升高至500 ℃，此為快速升溫階段；當舵面溫度達到500 ℃后保持恒溫狀態100 s；之后關閉加熱系統，此為自然降溫過程。試件溫度變化曲線如圖6所示。在以上加熱、恒溫和降溫過程中，數據采集系統同時對舵面結構進行激勵，并采集振動響應數據。

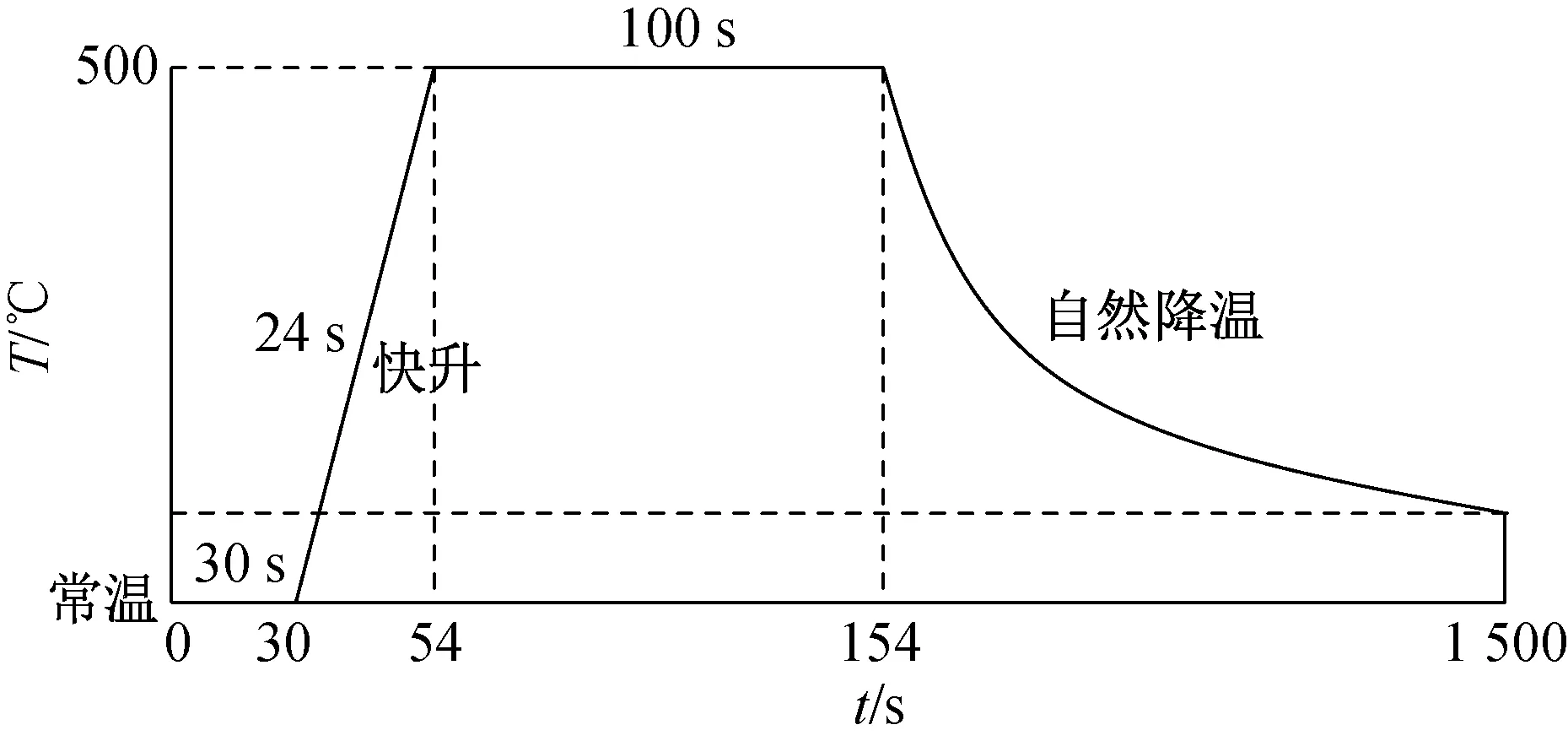
圖6 試件溫度變化曲線Fig.6 Temperature curve of test structure

從上一節對仿真模型的辨識結果來看，NIC算法的抗噪聲能力更強，因此采用該算法對舵面結構進行辨識。由于結構表面溫度迅速升至500 ℃，而結構自身參數的變化要滯后于這樣的快速變化，因而選取前50 s進行辨識。利用NIC算法辨識出的前四階結果如圖7所示。從圖中可以看出，隨著溫度升高，各階固有頻率均出現了不同程度的下降。第一階固有頻率在初始時刻和跟蹤結束時擾動較大，這主要與本試驗中低頻加速度信號幅值較小有關；更高階頻率的辨識值相對穩定，能反映結構固有頻率隨溫度變化情況。實驗結果表明：NIC算法可用于熱模態分析，對加速度響應幅值較高的頻段辨識效果較好；基于NIC子空間跟蹤的模態參數辨識方法可用于有激勵信號的情況，當激勵信號為白噪聲時，該方法可轉換為僅利用響應數據進行辨識的運行模態分析方法。

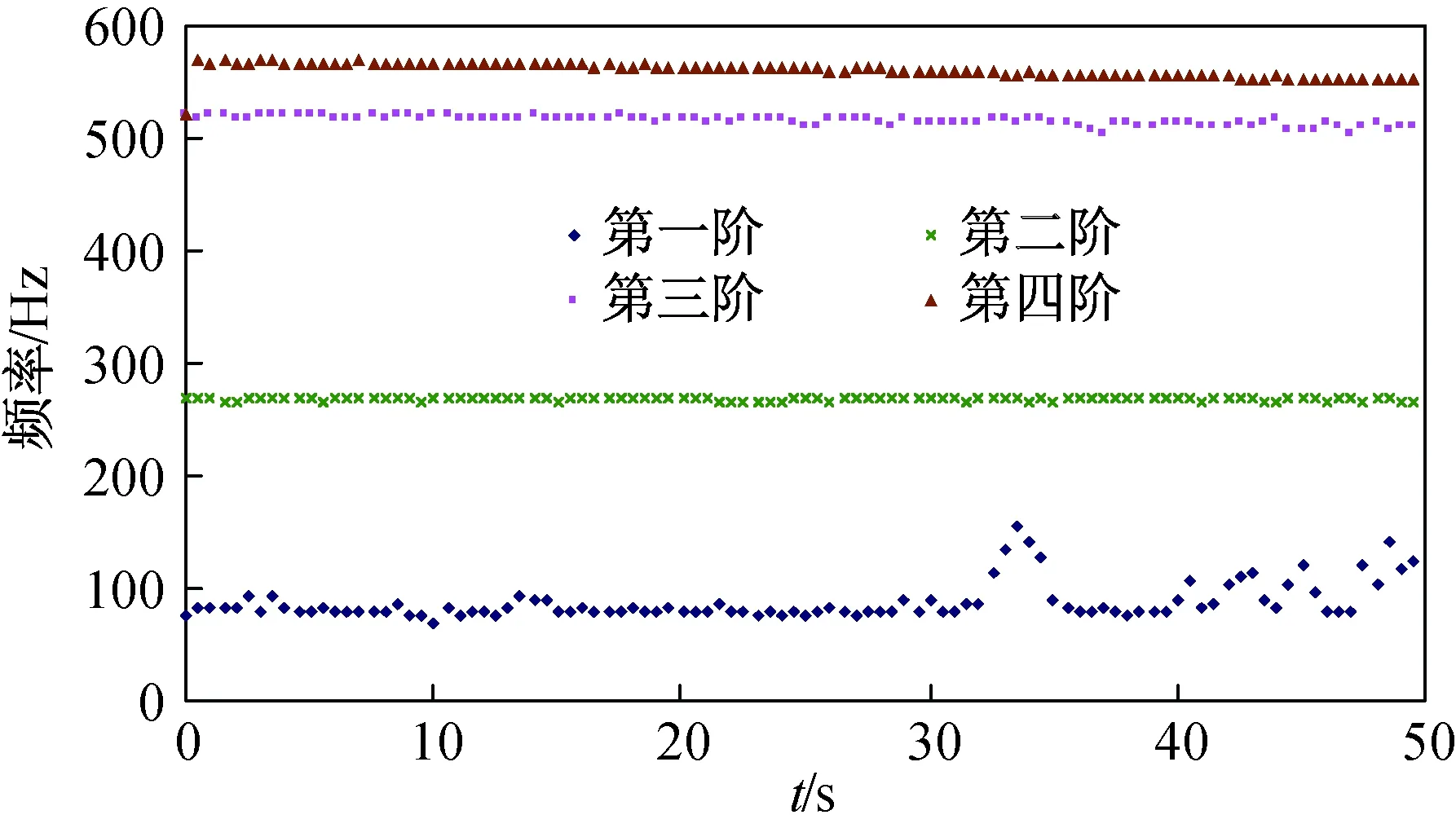
圖7 前四階辨識結果Fig.7 Identification results of first four orders

4 結束語

本文總結了子空間算法的一般步驟，結合一個有理論參考解的時變兩自由度彈簧-質量模型考察了4種子空間算法的辨識精度，結果發現NIC算法的抗噪能力較強。利用能夠對飛行器舵面結構進行受控加熱的實驗裝置采集了舵面結構在快速升溫過程中的加速度響應數據，并僅利用響應數據進行了時變模態參數辨識。辨識結果表明：基于NIC子空間跟蹤的模態參數辨識方法適用于熱模態分析，對振動響應幅值較高的頻段辨識效果較好，具有一定的工程應用價值。但受子空間類算法本身所限，模型定階、計算參數選擇等問題仍待解決。