彈道跟蹤數據野值剔除方法性能分析

侯博文，王炯琦,2，周萱影，李 冬，何章鳴,2

(1.國防科技大學理學院，長沙 410072； 2.北京控制工程研究所，北京 100086；3.中國人民解放軍91550部隊94分隊，大連 116023)

0 引言

高精度彈道跟蹤數據是分析和鑒定航天飛行器的制導系統、再入系統、測控系統及其它分系統的重要基礎。然而，無論采用何種彈道跟蹤體制對飛行器進行跟蹤測量，跟蹤或測量設備的沖擊、振動、系統故障、環境干擾，或操作人員的誤判等都會造成過失誤差，引起異常值。測量數據集合中偏離正常數據所呈現趨勢的數據點稱為野值[1]。野值的存在會嚴重影響彈道跟蹤數據的精度，甚至歪曲測量體系真相，在需要高精度彈道跟蹤數據的場合是不允許的。因而，必須在彈道跟蹤數據預處理中，檢測、識別野值，并剔除或作必要的修正。

根據野值是否連續，可分為孤立型和斑點型野值[2]。根據彈道跟蹤數據處理模式又可分為事后處理和實時處理。不同情況下跟蹤測量數據的野值特征、表現形式、變化規律各不相同。目前已經有很多學者提出了不同的野值剔除方法[3-10]。傳統的野值剔除方法[3](包括萊特準則、羅曼諾夫斯基準則、格拉布斯準則及肖維勒準則等)對于彈道數據的統計特性具有約束性，導致這些方法在使用時受限；自適應最小二乘法[4]對于孤立型野值具有較好的剔除效果，但沒有討論關于斑點型野值處理效果；中值濾波差分法[7]可有效剔除斑點型野值，但剔除效果不穩定，會出現數據失真或缺失的情況；外推擬合法[8]可有效剔除孤立型和斑點型野值，但斑點型野值剔除后會出現數據缺失；插值剔除法[9]適用于光學測量設備，在其他情況下效果并不顯著。

本文對上述文獻中提到的各種野值剔除方法進行了綜述，從理論上分析了各種方法的優缺點，基于各野值剔除方法建立了相應的識別準則和剔除步驟，并通過仿真分析了其針對孤立型野值和斑點型野值的剔除能力，對比了各類野值剔除方法效果，為實際工程應用提供了理論與技術支撐。

1 事后數據野值剔除方法

彈道跟蹤數據的事后野值剔除是指在導彈或火箭飛行試驗后對彈道測量數據的野值剔除。

假設測量數據序列為y=[y1y2…yn]Τ，其可以表示為

(1)

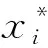
由于飛行器的飛行數據一般是具有趨勢的數據，因此事后野值剔除主要分為兩步，即趨勢剔除(包括真實信號特征提取、系統誤差補償等)和野值剔除。這里主要介紹野值剔除的方法。假設趨勢剔除后的數據為x=[x1x2…xn]Τ，趨勢剔除后的測量數據殘差序列為v=[v1v2…vn]Τ。工程中常用的有以下幾種事后野值處理準則。

1.1 萊特準則

萊特準則是最常用、最簡單的判別準則，該方法以測量次數充分大為前提[11]。

原理：對于某一個測量序列，假設各測量值只含有隨機誤差，則根據隨機誤差的正態分布規律，其殘差落在3σ以外的概率不超過0.3%。

準則：以3σ為野值判斷閾值，其中σ為測量殘差v的標準差。

步驟如下：

1) 計算剔除趨勢后數據均值及標準差為

(2)

2) 計算各個時刻數據的殘差，有

(3)

3) 將殘差逐一與3σ進行比較，若

vi≥3σ

(4)

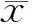
1.2 羅曼諾夫斯基準則

羅曼諾夫斯基準則又稱為t檢驗準則，對于一批獨立等精度測量數據中存在單個異常值的情況，是一種有效的識別方法[12]。

原理：根據抽樣分布定理，按照t分布的實際誤差分布范圍來檢測野值。

準則：根據樣本確定的檢測統計量與給定顯著水平下確定的t檢驗系數進行比較，確定野值。

步驟如下：

1) 根據抽樣分布定理，確定服從t分布的隨機變量，有

(5)

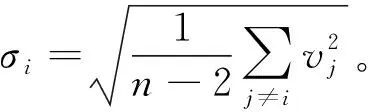
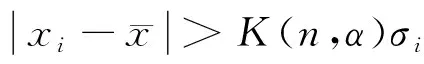
1.3 格拉布斯準則

格拉布斯準則又稱極大殘差檢驗[14]，是檢測服從正態分布的單變量數據集中野值的方法。

原理：將測量值由大到小排序，依次進行野值剔除。

準則：確定構造統計量的分布，根據預設的顯著性水平剔除野值。

步驟如下：

1) 將xi按大小順序排列成順序統計量x(i)，滿足

x(1)≤x(2)≤…≤x(n)

(6)

2) 構造統計量

(7)

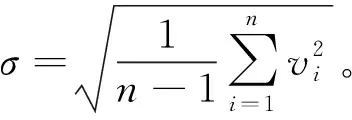
3) 取定顯著性水平α，有

P(gn≥G(n,α))=α

(8)

其中格拉布斯確定了g分布的臨界值[11]，有

(9)

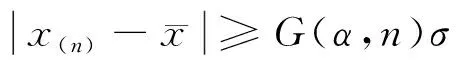
1.4 肖維勒準則

肖維勒準則以正態分布為前提，是一種剔除實驗數據中野值的有效方法[15]。

原理：設在一個n次的等精度測量中，不出現vi>a的誤差，那么概率P{vi>a}接近于0。當n足夠大時，由大數定律，概率P≈m/n，其中m是vi>a出現的次數。因此可認為

m/n?P{vi>a}→0

(10)

或

m?nP{vi>a}→0

(11)

式中：m為整數。因此有

nP{vi>a}≤1/2

(12)

即最低限度應有

P{vi>a}=1-erf(k)=1/(2n)

(13)

式中：k=a/σ，k值可查表[16]獲得。

準則：確定一個概率范圍，其中心為一個標準正態分布的均值，在該范圍之外的點即可判斷為野值。

步驟如下：

1)計算數據殘差vi。

2)剔除野值，如滿足

vi>kσ

(14)

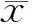
1.5 奇偶提取法

奇偶提取法，即將數據按照奇偶位置分為若干組(集)進行野值剔除[17]。

原理：原數據樣本標準差誤差較大，將原數據拆分成小樣本數據集后，每個小樣本數據集中野值個數減少，標準差更接近于真值。

準則：分組后的數據按照萊特準則進行野值剔除。

步驟如下：

1) 奇偶序列提取。對于數據x1,x2,…,xn按照奇偶位置分成兩組，分別記為x1-O,x1-E；再進行第二次分組，得到x2-OO,x2-OE,x2-EO,x2-EE；以此類推，將數據x1,x2,…,xn分成2m組。

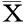
(15)

(16)

(17)

(18)

以此類推，根據需要選定分組次數m(根據精度設定)，分成2m個小樣本數據集，對每組都進行上述求均值和方差的過程。

3) 利用萊特判別準則進行野值檢驗和剔除。

4) 數組整合。

經過步驟1)～3)后，將剔除野值后的分組數據進行整合，得到完整的數據。

需要注意的是，在每組小樣本數據集里可能存在第1個數據就是野值的情況，此時用第2個數據替代。

1.6 差分輔助中值濾波

在中值濾波的基礎上借差分思想對數據進行野值剔除。

原理：對測量數據進行一次差分，可得

(ωi+1-ωi)+(δi+1-δi)

(19)

考慮野值差分結果為(δi+1-δi)，對于斑點型野值，若野值點幅度相近，在差分數據中，野值點數據將只保留在當前窗口內的第1個野值數據，其余野值將會被差分消除。因此，斑點型野值會變為孤立型野值。孤立型野值可直接利用中值濾波方法進行剔除。

準則：對一次中值濾波后的觀測數據進行一次差分，對差分后的數據再進行中值濾波，積分還原后進行野值判斷。

步驟如下：

1) 對原始測量數據x進行中值濾波得到xmed，剔除外彈道測量數據中的孤立型野值。

2) 對xmed進行一次差分后，再進行一次中值濾波剔除野值。

3) 對差分后的數據進行積分，得到原測量數據。

4) 檢測剔除后的數據是否還存在野值，如有，重復步驟1)～3)。

2 實時數據野值剔除方法

彈道跟蹤數據的實時野值剔除是指在導彈或火箭飛行試驗過程中，對彈道測量數據的野值進行實時檢測與剔除[4]。

由于實時數據的獲取會有延遲，所以實時數據野值剔除也主要分為兩步，即數據外推和野值剔除，此外，還要求起始段數據無野值情況。

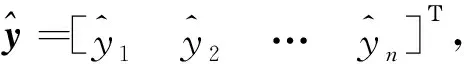
2.1 五點線性預報野值剔除法

五點線性預報法分為差分檢驗、線性預報。首先用求一階差分和四階差分的方法對數據進行合理性檢驗，發現并剔除明顯的野值點，并按五點線性預報公式補點。

原理：利用最小二乘法對數據進行預報，與實測數據做對比，從而實現野值剔除。

準則：將測量數據殘差與預先確定的野值檢測門限做對比并進行檢測。

步驟如下：

1) 對跟蹤數據進行一階差分，其表達式為

Δ1yi=yi+1-yi

(20)

用四階差分檢驗法進行初始檢驗，找出一組合理點。

2) 數據四階差分值

Δ4yj=yj-4-4yj-3+6yj-2-4yj-1+yj

(21)

式中：j≥5。取門限值M1(經驗值為17σ，σ為測量數據的精度)，判斷Δ4yj≤M1是否成立，若是，則為一組合理點；否則，令j=j+1，繼續進行四階差分檢驗。

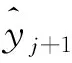
(22)

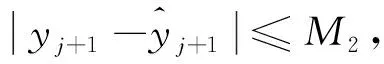
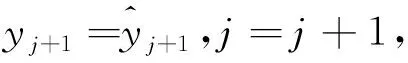
2.2 α-β-γ濾波器野值剔除法

原理：利用α-β-γ濾波器對數據進行預報，與實測數據做對比，從而實現野值剔除。

準則：將測量數據殘差與預先確定的野值檢測門限做對比并進行檢測。

步驟如下：

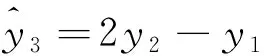
(23)

式中：u，s為濾波器的中間變量。

2) 從第4點開始按照式(24)、(25)遞推計算，有

(24)

(25)

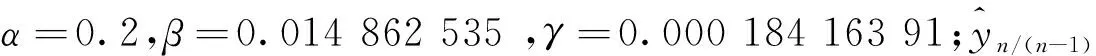
3) 對測量數據序列進行一步預測，若實測值與預測值之差的絕對值小于某門限值，此數據為合理值，反之為野值。

(26)

式中：M為門限值，一般為正常訓練數據預測殘差精度的3倍。

2.3 基于穩健估計的自適應門限法

由于數據中存在的野值會影響樣本標準差的確定，結合穩健估計原理，實時確定野值檢測門限，從而實現跟蹤數據的野值實時剔除[18]。

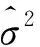
(27)

式中：ψ(·)為影響函數；β為待定參數。適當選擇ψ(y)和β可對數據中異常值加以抑制。

2)β公式的推導。選擇Huber的ψH(y0)函數作為影響函數，有

(28)

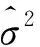
(29)

因為異常值不多且可用CΗσ代替，故有

(30)

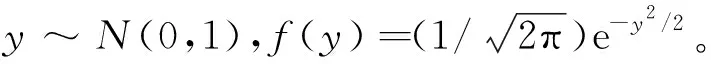
(31)

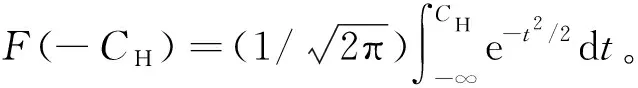
因此取不同的CH有不同的β，在實時數據處理過程中一般取CH=1.5，此時β=0.778 5。又有

(32)

于是有

(33)

(34)

式中：∑1為滿足Δyi≤CHσ的觀測數據求和；NH為觀測數據中Δyi>CHσ的數據個數；n為窗口大小，通常取16～30。由于實測數據是動態的，故采用滑動數據窗口。

準則：將測量數據殘差與實時更新的野值檢測門限做對比，實現野值檢測和剔除。

步驟：

2) 判斷是否滿足Δyi≤CHσ，若滿足，則yj+1為合理值；否則，為野值，用預測值代替。

2.4 基于匹配測元的方法

彈道跟蹤數據中存在匹配關系的測元，如某一個測元是另一個測元的微分(或積分)，根據某一測元的正常數據來剔除另一測元測量數據的野值。

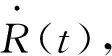
(35)

式(35)為匹配測元之間的關系，可改寫為

(36)

在實際測量數據中，由于系統誤差和隨機誤差，有

(37)

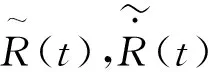
(38)

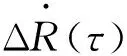
準則：測量和匹配數據的殘差與設定的野值檢測門限做對比，實現野值檢測和剔除。

步驟如下：

1) 選取連續n個點的匹配測元數據，計算

(39)

并進行統計，有

(40)

若ΔL(t1)>3σ，則R(t1)為野值點，其中σ為數據精度。記野值點個數為l，則有

(41)

2) 以n點為窗口滑動，按照步驟1)進行數據檢測。

3 仿真驗證

針對實際彈道跟蹤測量存在的孤立型野值和斑點型野值，分別就事后處理和實時處理2種模式，進行野值剔除的仿真計算。為了更好地描述每種方法的性能，定義野值剔除率為

(42)

3.1 事后數據野值剔除仿真

用計算機仿真出200個服從均值為0，方差為2的剔除趨勢后的數據點，在第96～105個點間加入常值為10的野值(斑點型野值)，在第50、70、130、150個點分別加入常值為-15、-10、15、12的野值(孤立型野值)。為更好地體現各方法的性能，在第151～160個點間加入了10sin(i)的斑點型時變野值，i為時間。分別用第2節中的6種方法進行野值剔除，顯著性水平設置為0.01，進行了10次仿真，取某一次仿真結果如圖1所示。圖1(a)～(d)中紅線為野值檢測閾值，藍線為數據殘差；圖1(e)～(f)中紅線為剔除野值后數據，藍線為剔除野值前數據。

10次仿真的數據野值剔除率和誤檢點數統計結果見表1。

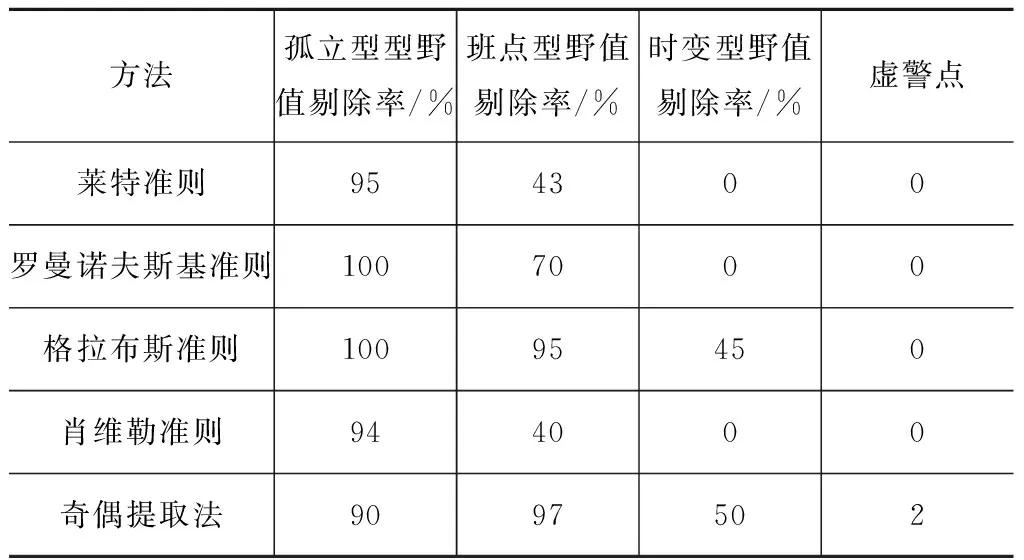
表 1 事后數據野值檢測結果

差分輔助中值濾波法是直接將野值剔除，故無法判斷野值檢測結果。從圖1(f)可看出，該方法在一定程度上可實現野值剔除，但該方法受數據本身波動影響較大，當原始數據出現較大波動時，野值剔除后的數據也會出現波動，效果不穩定。

綜合表1中準則，結合仿真結果，得到各種方法對比結果見表2。

3.2 實時數據野值剔除仿真

設定二次多項式仿真彈道數據

y(t)=0.4×t2+5×t+220

(43)

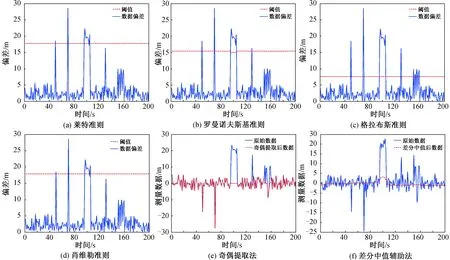
圖1 事后數據野值剔除結果Fig.1 Results of off-line data outlier elimination

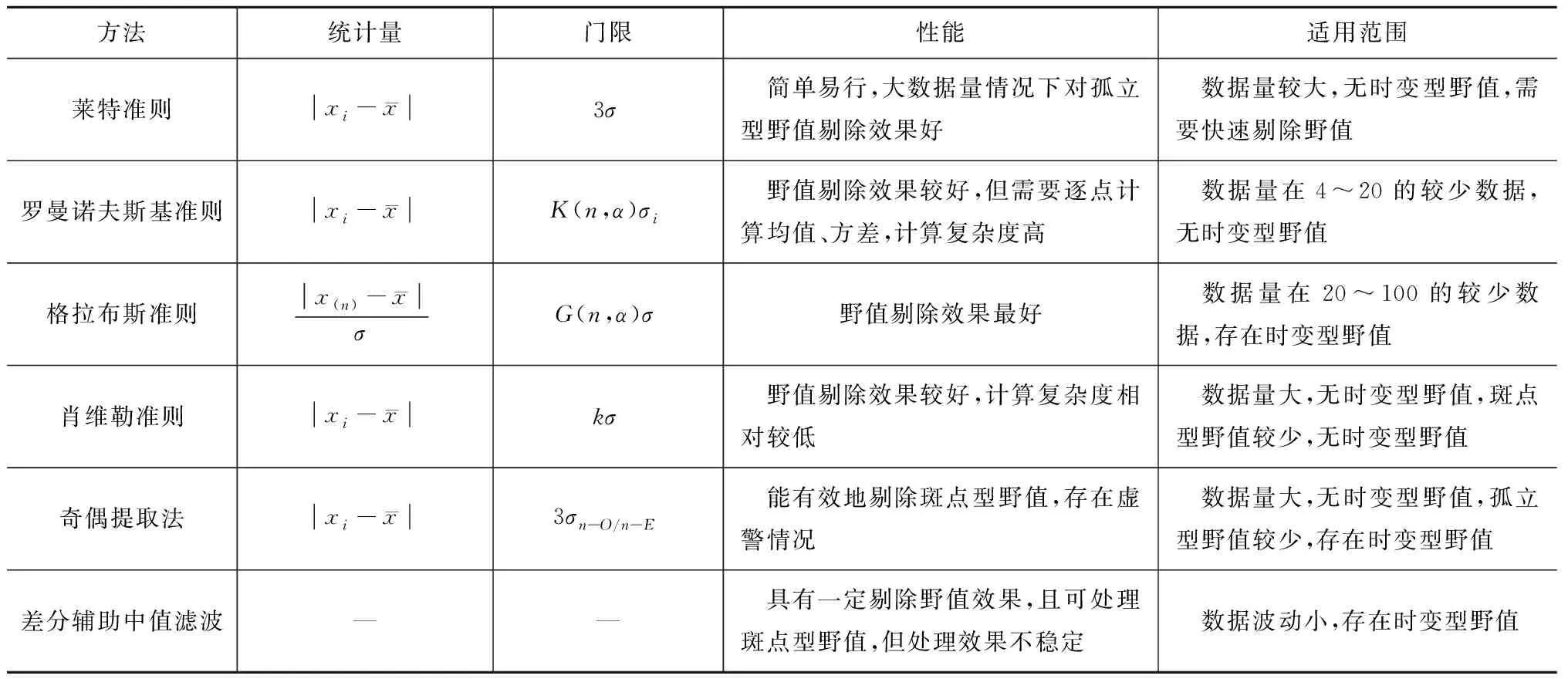
方法統計量門限性能適用范圍萊特準則xi-x3σ 簡單易行,大數據量情況下對孤立型野值剔除效果好 數據量較大,無時變型野值,需要快速剔除野值羅曼諾夫斯基準則xi-xK(n,α)σi 野值剔除效果較好,但需要逐點計算均值、方差,計算復雜度高 數據量在4～20的較少數據,無時變型野值格拉布斯準則x(n)-xσG(n,α)σ 野值剔除效果最好 數據量在20～100的較少數據,存在時變型野值肖維勒準則xi-xkσ 野值剔除效果較好,計算復雜度相對較低 數據量大,無時變型野值,斑點型野值較少,無時變型野值奇偶提取法xi-x3σn-O/n-E 能有效地剔除斑點型野值,存在虛警情況 數據量大,無時變型野值,孤立型野值較少,存在時變型野值差分輔助中值濾波—— 具有一定剔除野值效果,且可處理斑點型野值,但處理效果不穩定 數據波動小,存在時變型野值

式中：y(t)為位置數據；t為時間。共設200個采樣點，采樣時間間隔為0.05 s，野值與事后處理仿真設定相同，共進行10次仿真，取某一次仿真結果如圖2、3所示。圖2中紅線為檢測門限，藍線為預測殘差；圖3中紅線為剔除野值后數據，藍線為剔除野值前數據。

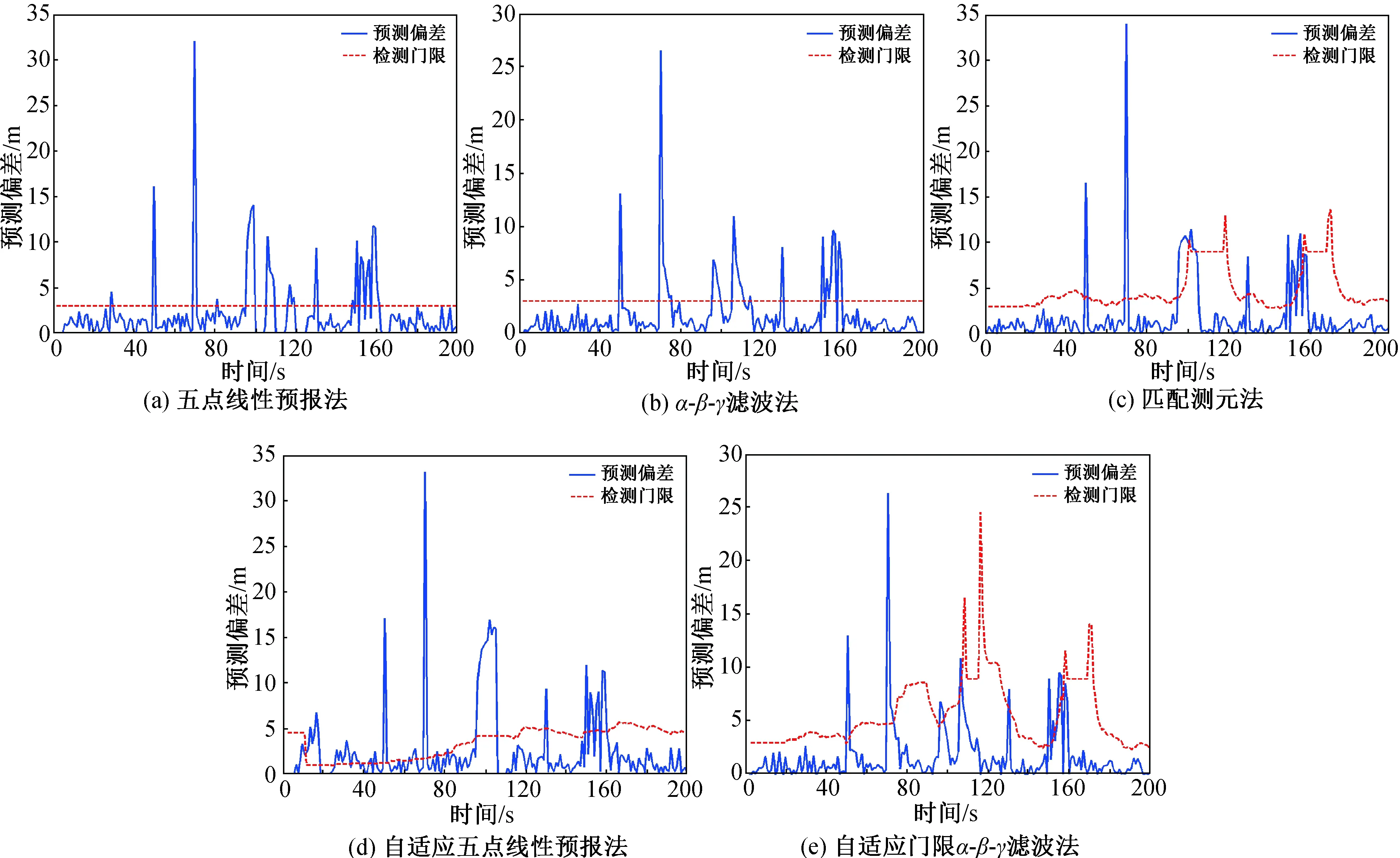
圖2 實時數據野值檢測結果Fig.2 Results of on-line data outlier detection

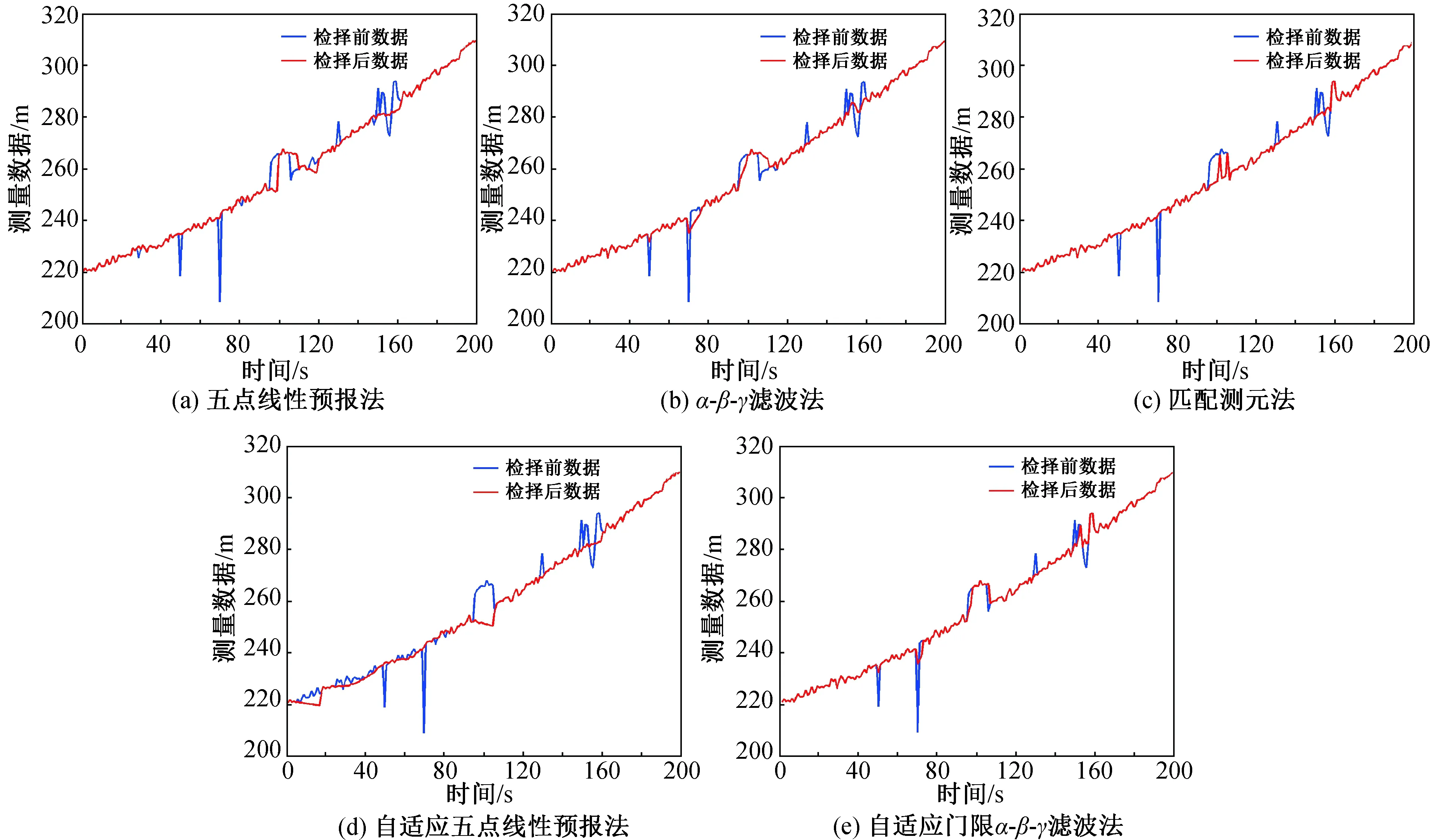
圖3 實時數據野值剔除結果Fig.3 Results of on-line data outlier elimination

由于實時野值剔除方法對計算效率有較高的要求，因此幾種方法的時間復雜度和仿真運算見表3。

綜合以上幾種實時數據處理方法，并結合圖2、3及表3可得各種方法對比結果，見表4。

表3 實時數據野值檢測結果

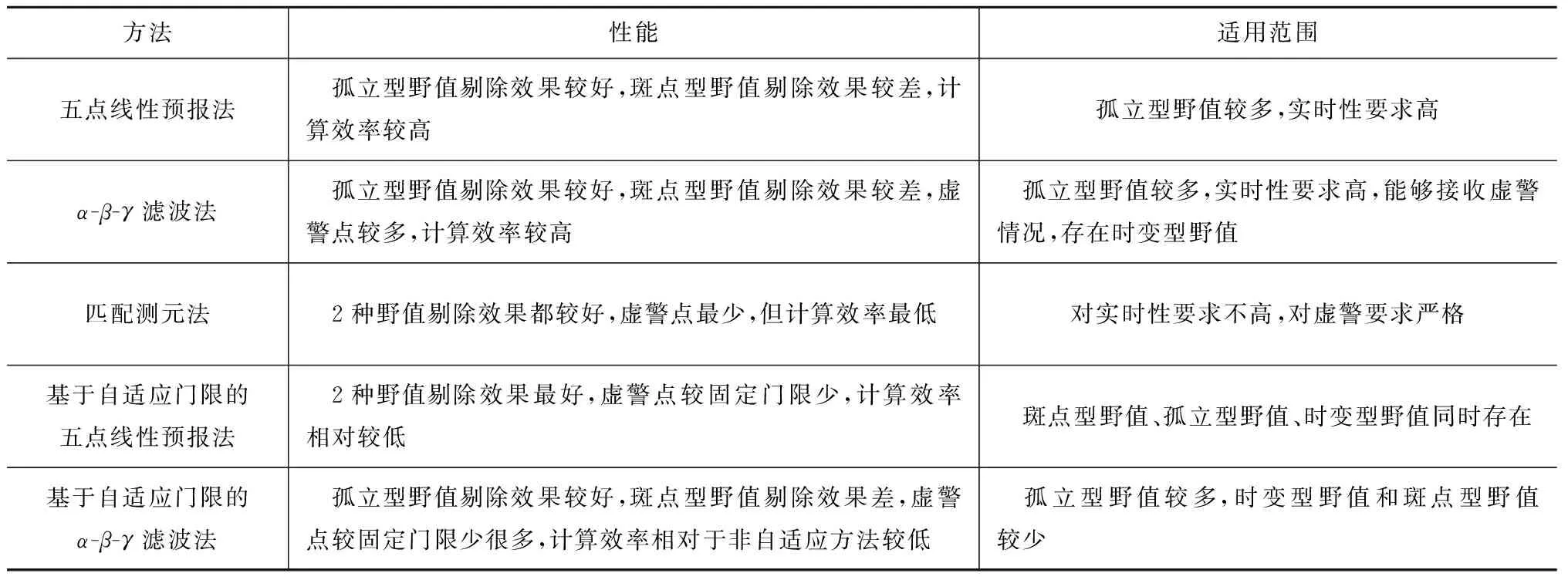
表4 實時數據野值剔除方法效果對比

4 結束語

野值剔除結果會直接影響彈道跟蹤數據處理的精度。本文結合彈道數據事后處理和實時處理2種模式，對常見的，用于彈道跟蹤數據的野值剔除方法進行了綜述。通過理論分析和仿真計算表明：不同的野值剔除方法對野值的剔除效果不同。在事后數據野值剔除中，羅曼諾夫斯基準則對斑點型野值和孤立型野值的剔除效果較好，但需要以犧牲計算效率為代價；肖維勒準則對于斑點型野值剔除效果較好，且計算效率高；萊特準則在數據量較大情況下對斑點型野值剔除效果較好；格拉布斯準則對于孤立型野值和斑點型野值剔除效果最好；奇偶提取法對于斑點型野值和時變型野值剔除效果較好；差分輔助中值濾波法在一定程度上具有剔除野值的作用，但效果不穩定。在實時數據野值剔除中，五點線性預報法比α-β-γ濾波法好，自適應門限方法比固定門限方法好，主要體現在虛警點少，剔除效率高。匹配測元方法的野值剔除效果僅次于基于自適應門限的五點線性預報法，且虛警點最少，但時間復雜度較高，實時性相對較差。當孤立型、斑點型、時變型野值都存在時，基于自適應門限的五點線性預報法能較好地實現野值剔除功能。

綜合比較可知：在事后處理中，對孤立型野值，羅曼諾夫斯基準則和格拉布斯準則可有效剔除；對斑點型野值，格拉布斯準則的剔除效果最好；對時變型野值，格拉布斯準則和奇偶提取法都能實現一定程度的剔除。考慮到各種方法的適用性，當彈道數據量較大時，對彈道數據的孤立型野值剔除也可選擇萊特準則；對斑點型野值和時變型野值可選擇奇偶提取法；在實時處理中，各種方法都能有效剔除孤立型野值，出于實時性要求，選擇五點線性預報法最佳；基于自適應門限的五點線性預報法對斑點型野值的剔除效果最好，效率最高；α-β-γ濾波法對時變型野值的剔除效果最好；如果3種野值同時存在時，采用基于自適應門限的五點線性預報法最合適。