基于觀測器的上面級姿控發動機時間滯后補償控制方法

陳海朋，于亞男，余薛浩，黃 飛

(上海航天控制技術研究所，上海 201109)

0 引言

上面級執行任務通常需要大角度快速機動，這是一個非線性系統的控制問題。由于傳統歐拉角描述姿態系統的運動存在著奇異性，而四元數法可克服這種奇異性，因而其在描述大角度機動飛行的姿態運動時得到了廣泛的應用[1]。

大角度機動姿態控制方法包括基于李亞普諾夫理論的控制、滑膜變結構控制、解耦控制、誤差四元數控制等。目前國內外學者已開展了相關研究，如：WIE等[2]研究了繞歐拉軸轉動的四元數反饋控制器，給出了在始末端靜止條件下由誤差四元數和星體角速率線性組合構成的反饋控制律，確保星體繞歐拉軸轉動，從而獲取最佳的機動性能，證明了其全局穩定性；CREAMER等[3]根據歐拉定理規劃出繞歐拉軸快速機動的標稱姿態，將星體真實姿態和標稱姿態的差值作為反饋信號，設計了用以姿態跟蹤控制的PID(比例、積分、微分)控制器，完成了大角度機動；鄭立君等[4]針對撓性衛星的大角度機動，提出了基于拋物線型角加速度的曲線路徑，設計了正弦函數角加速度曲線，解決了快速機動和高精度穩定問題。上述學者在姿態路徑規劃時均未考慮初始角速度干擾，本文在考慮初始干擾的在線四元數路徑規劃和誤差四元數控制方案的基礎上，實現全向姿態路徑規劃和穩態跟蹤，并重點介紹了姿控發動機響應延遲的補償控制方法。

目前航天器常用的姿態控制執行機構有姿控發動機、力矩陀螺、飛輪等。上面級的慣量較大，當其進行姿態大角度機動控制時，常將姿控發動機作為執行機構。姿控發動機輸出為常值推力，而控制器求解出的控制量要求姿態控制執行機構為變推力，實際中采用控制姿控發動機開關時刻和持續時間來實現。目前實現變推力的主要方法有脈沖寬度調制、脈沖頻率調制、脈寬脈頻調制等，在工程實現上分別對應斜開關線控制、開關控制、脈寬脈頻調制控制。其中：斜開關線控制多用于衛星初始姿態穩定和軌道控制，建立穩定姿態后，采用飛輪等連續的精確的控制機構，其控制參數理論推導較難，參數設計多依靠經驗及仿真確定；脈寬脈頻調制控制調節器的設計參數多，頻域穩定性分析困難，在干擾狀態下開關頻繁，因此在航天器上應用很少。因此，本文采用開關控制方式。

控制器控制信號發送到姿控發動機產生推力存在一定延遲時間，該時間對系統控制不利，特別對控制精度造成很大影響。延遲時間越大,對系統性能的影響越大。國內外學者已針對姿控發動機延遲時間對控制精度的影響開展了相關研究。如：楊忠等[5]研究了延遲時間變化和一致性對控制精度的影響，發現減少延遲時間可提高姿態控制精度；劉慶鴻等[6]分析了控制系統延遲時間對制導精度的影響，發現為滿足制導精度，需要將發動機延遲限定在一定范圍內。衛星一般采用多種執行機構聯合控制的方式實現高精度的姿態控制，而目前國內外缺少對姿控發動機延遲補償控制研究。因此，研究時間滯后補償控制，減小姿控發動機響應延遲對控制精度的影響，對于上面級長期在軌高精度飛行具有重要意義。

當前國內外學者已開展了大量關于純滯后系統控制的研究，常用方法有Dahlin控制算法和Smith預估算法。Dahlin控制器對被控對象數學模型參數誤差的敏感度較低，只要模型參數誤差在合理范圍內，就均能對被控對象實現有效控制，其設計核心思想是將閉環傳遞函數假設成一階慣性環節與滯后環節串聯的形式，該方法仍要獲取被控對象的模型參數[7]。Smith預估算法通過預估控制器對滯后時間進行補償，使閉環特征方程不再包含純滯后項，從而可以按照非滯后系統的方法進行處理，減小系統超調量，加速系統的調節過程[8-10]，而Smith預估器對被控對象的數學模型具有很嚴格的要求，對參數的不確定性、擾動及時變時滯等特征都很敏感[10-11]。目前預估模型參數多采用離線參數辨識方法獲取，基于非線性規劃函數Fminsearch辨識方法[12]和基于BP神經網的參數辨識方法[13]均為離線辨識方法，不能對系統模型參數實時修正，且步驟過于復雜，不易實現。上面級受燃料消耗和衛星分離影響，質量特性具有時變性，離線獲取的預估模型與實際模型難以匹配。基于觀測器的控制方法可以預測系統狀態變量，對被控對象模型參數偏差敏感度低[13-14]，與Smith預估器結合使用，能有效解決Smith預估器對模型參數敏感的問題。

姿控發動機響應延遲導致姿態控制精度降低。為解決該問題，本文采用Smith預估補償方法，對延遲特性進行補償，采用魯棒觀測器對被控對象輸出進行觀測，并考慮模型的不確定性，引入補償控制量，使控制輸出觀測值更為精確，降低了Smith預估器對被控對象模型敏感度，并對提出方法進行了仿真驗證。

1 上面級姿態動力學模型

上面級的姿態動力學模型一般表示為

(1)

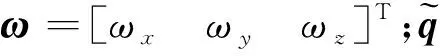
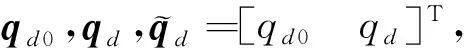
(2)

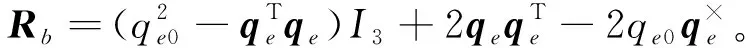
2 響應延遲對姿態控制的影響

姿控發動機是上面級姿態控制系統的執行機構，其輸出為常值推力形式，工作時輸出一定大小的推力，實際應用中只能依靠選擇其開關時刻和持續時間進行控制，發動機本身具有典型的非線性，為便于研究，將控制量轉化為開關控制量，發動機處于Bang-Bang(繼電器式控制)工作狀態，使發動機輸出推力脈沖為控制提供動力。

上面級姿態控制設計為

u= -kpqe-kdωe+ω×Jω，

kp>0，kd>0

(3)

式中：kp為PID控制比例系數；kd為PID控制微分系數。

本文采用脈沖頻率調制方法。其優點是控制簡單，缺點是存在響應滯后。本文方法的工作原理如圖1所示。圖中：u為開關控制器的控制量；d為電磁閥的門限值；δ為電磁閥滯環寬度；τ0為控制延遲時間。

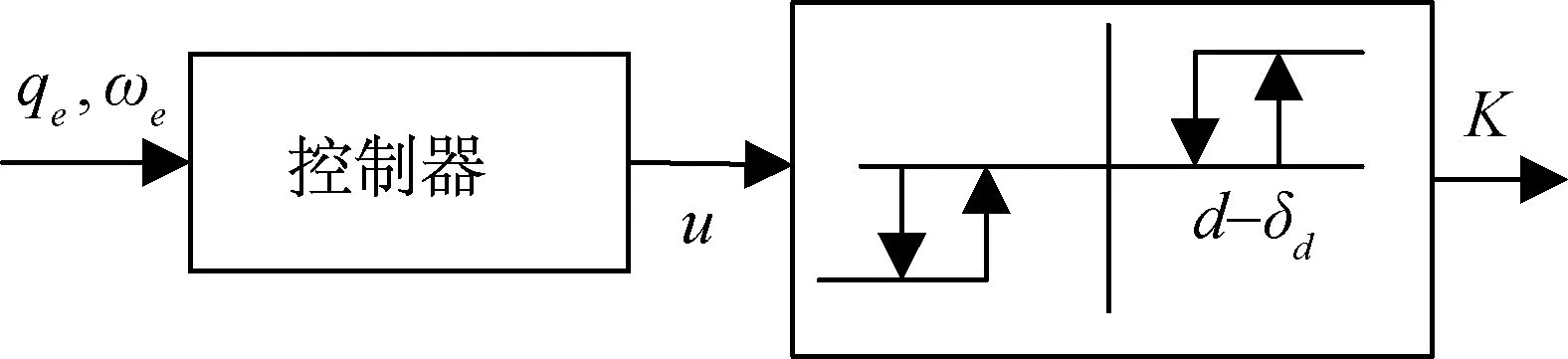
圖1 開關控制原理Fig.1 Switching control principle

開關控制器特性一般可表示為K=

忽略通道間的干擾，系統在有外界干擾和時間延遲情況下的表達式為

(5)

式中：a0為推力力矩系數；Mb為干擾力矩系數；k為姿控發動機開關控制量。假設kp=2，則經過推導可得到極限環的表達式，即

(6)

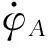
(7)

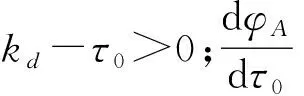
極限環曲線如圖2所示，圖中AEBCFD組成極限環。由圖可知：姿控發動機響應延遲使角速度控制精度降低，可增大kd，減小電磁閥滯環寬度δ，提高極限環精度，但會使系統抗干擾能力下降。

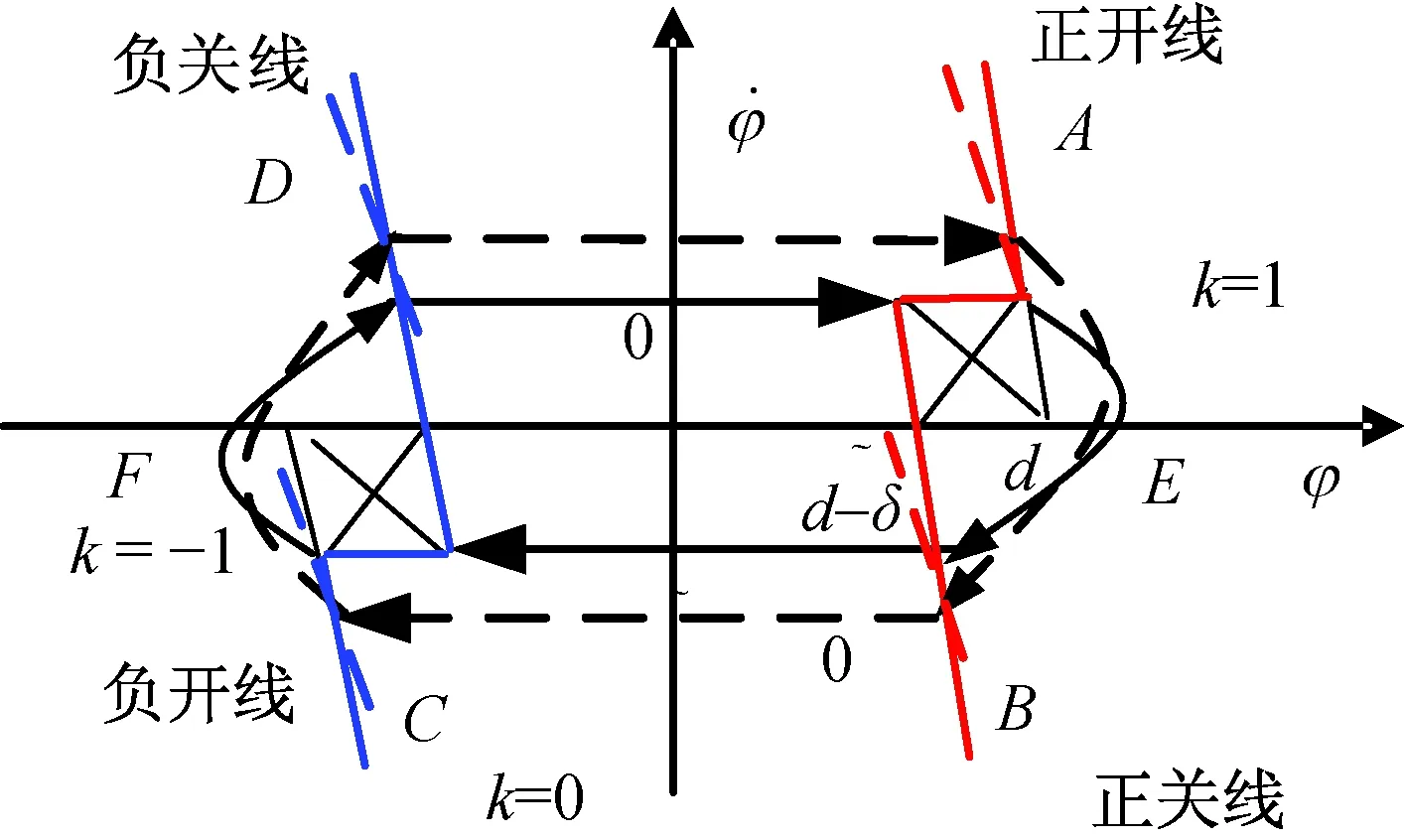
圖2 極限環曲線Fig.2 Limit cycle curve

3 基于觀測器的Smith預估補償

Smith預估算法是克服純滯后的有效控制方法，其基本原理是通過預估對象的動態特性，用一個預估模型來進行時間滯后的補償，預估模型與被控對象共同構成一個沒有時間滯后的廣義被控對象，從而有效克服純滯后[7]。Smith預估控制框圖如圖3所示。

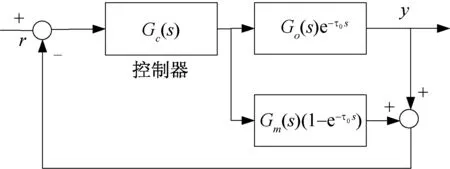
圖3 Smith預估控制框圖Fig.3 Block diagram of Smith predictor control

根據Smith預估控制原理，上面級單通道傳遞函數可定義為Go(s)e-τ0s，Smith預估模型為Gm(s)(1-e-τ0s)，則閉環傳遞函數

(8)

式中：D(s)= 1+Gc(s)[Gm(s)+

(Go(s)-Gm(s))e-τ0s]

(9)

由式(9)可知，當Smith預估模型與被控對象模型完全一致，即Gm(s)=Go(s)時,則系統特征方程中將不含有延遲部分。由于上面級的質量特性具有時變性，實際使用中難以獲取準確的模型參數，使得預估模型與實際模型難以匹配。本文采用魯棒觀測器代替原先預估模型，降低Smith預估補償對模型精確性的敏感度，Smith控制方法原理如圖4所示。

上面級的動力學模型可表示為

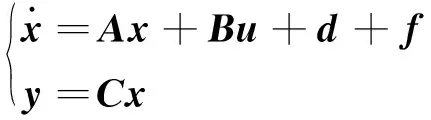
(10)

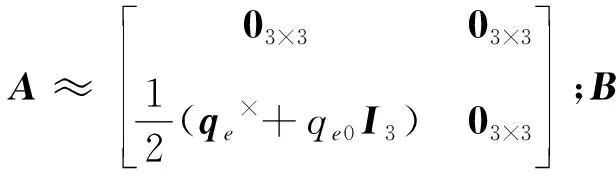
由于系統存在參數攝動和外擾動，設計魯棒觀測器為

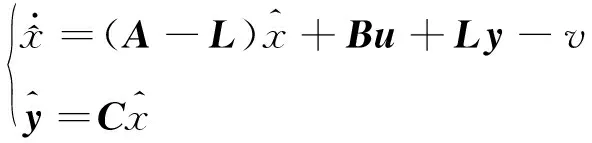
(11)

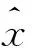
為證明觀測器的有效性，取對稱正定矩陣Q、矩陣P為李亞普諾夫方程的解，即

(A-L)TP+P(A-L)=-Q

(12)

觀測控制量為

(13)

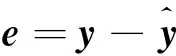
由式(10)、(11)得到誤差方程，其表達式為

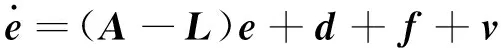
(14)

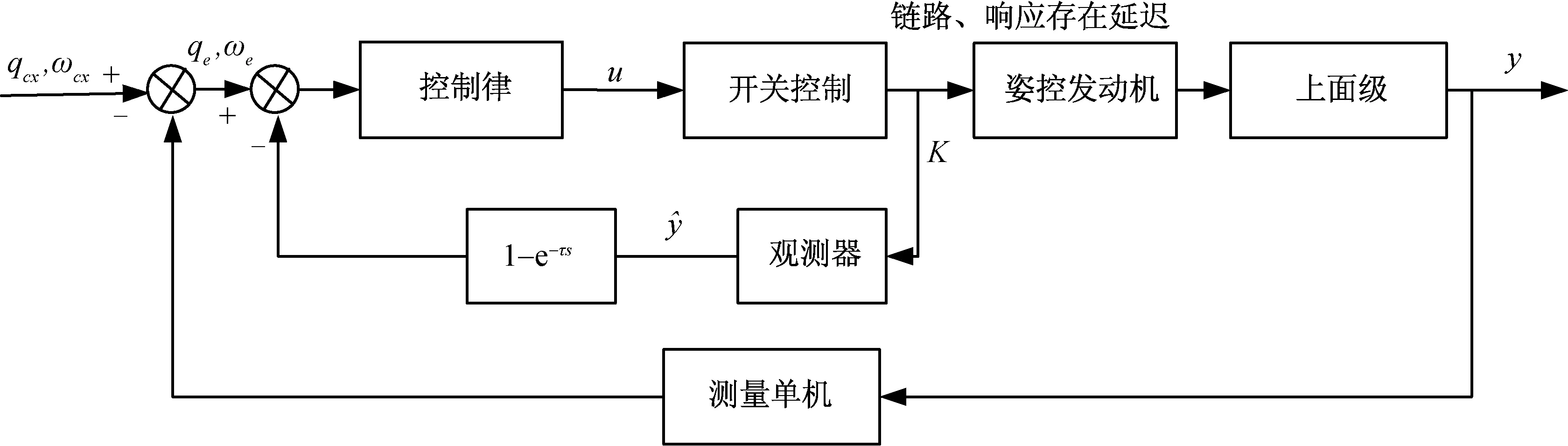
圖4 基于觀測器Smith補償控制原理Fig.4 Schematic diagram of Smith compensation control based on observer

取李亞普諾夫函數V=eTPe，微分可得

2eTP(d+f)+2eTPv

(15)

即

-eTQe+2‖P‖‖d+f‖‖e‖-

2η‖P‖‖e‖

(16)

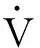
觀測器中加入干擾補償控制量，使觀測器對模型參數的準確性要求降低，觀測器的輸出值為yk，其表達式為

(17)

對式(17)離散化，得

(18)

式中：ΔT為控制周期；m為延遲周期個數。含有Smith預估控制輸出可描述為

(19)

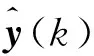
考慮上面級實際飛行過程中姿控發動機單次開關時間T較短(T≈0.1 s)，四元數增量與角速度增量比值約為0.5T，相差2個數量級，預估補償量可簡化為

(20)

4 仿真

假設數學仿真條件為：轉動慣量參數Jxx=3 000 kg·m2，Jyy=Jzz=4 500 kg·m2；姿控發動機推力為25 N；力臂長度lg=1.4 m；狀態反饋參數Kp=2,Kd=4；極限環控制參數Eom=4.5 °,m=0.95；姿態發動機延遲時間為80～200 ms；控制周期為40 ms。仿真曲線如圖5～7所示。

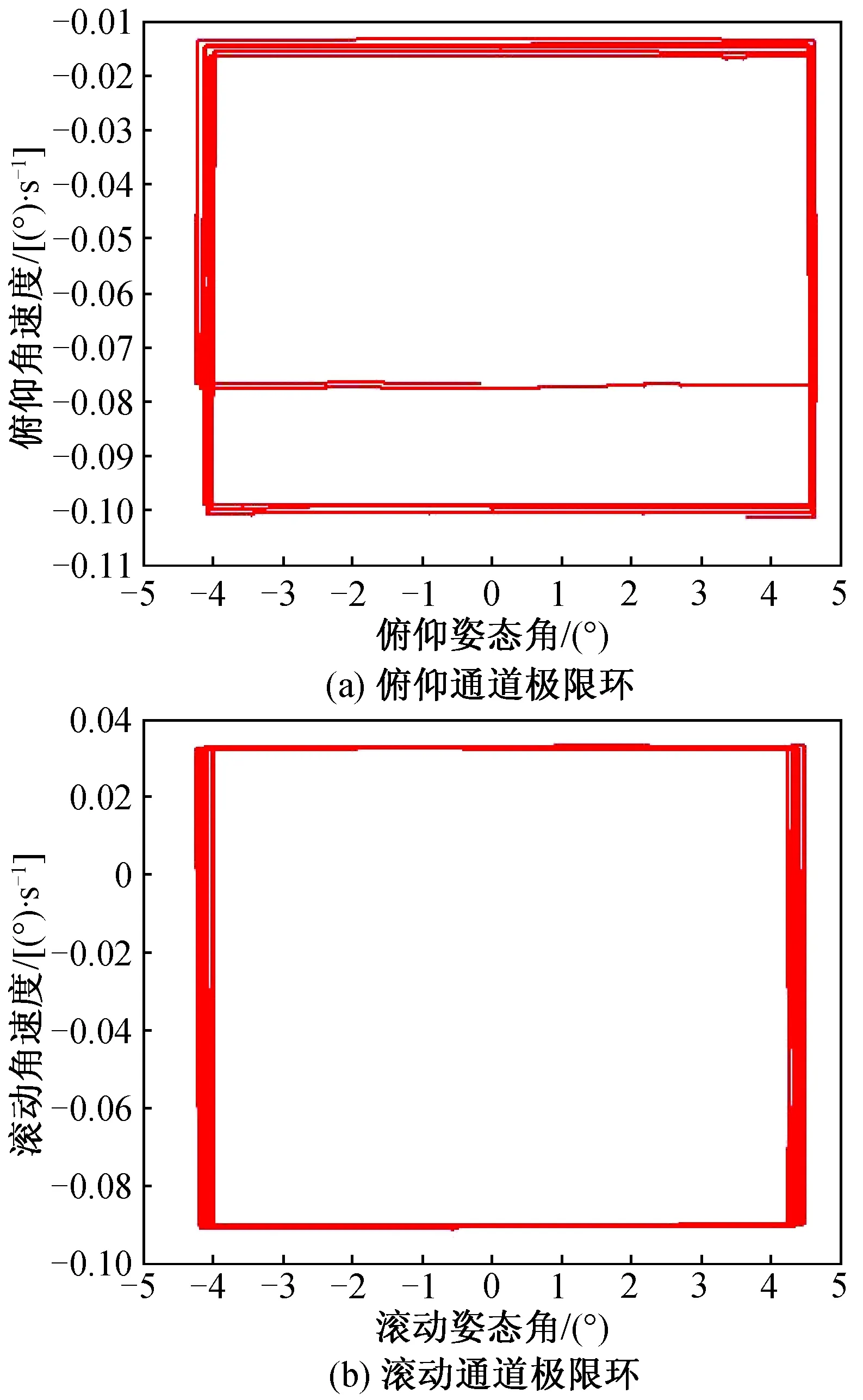
圖5 未考慮延遲時間極限環曲線Fig.5 Limit cycle curve without considering time delay

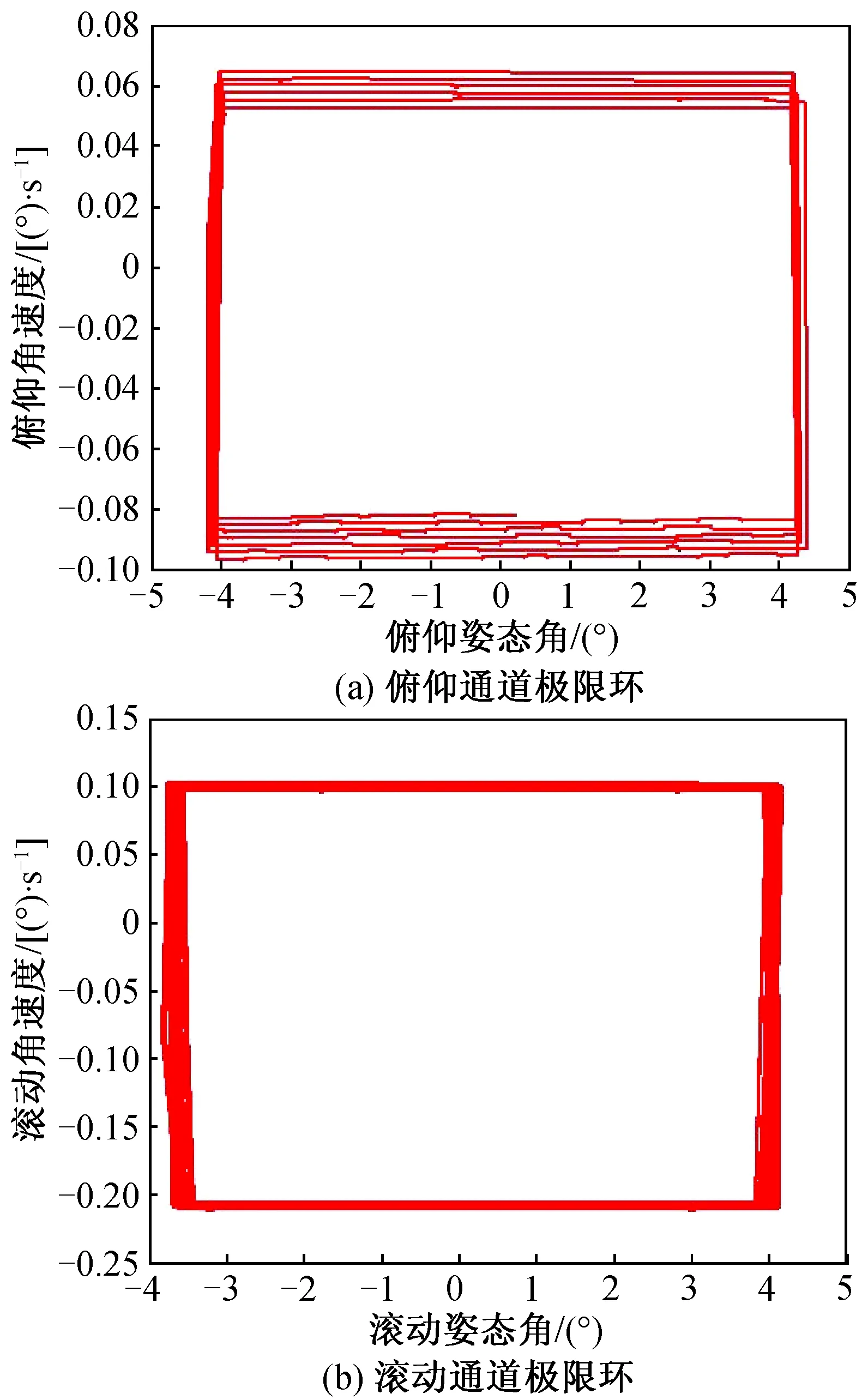
圖6 延遲160 ms未補償控制極限環曲線Fig.6 Limit cycle curve before compensation with time delay of 160 ms

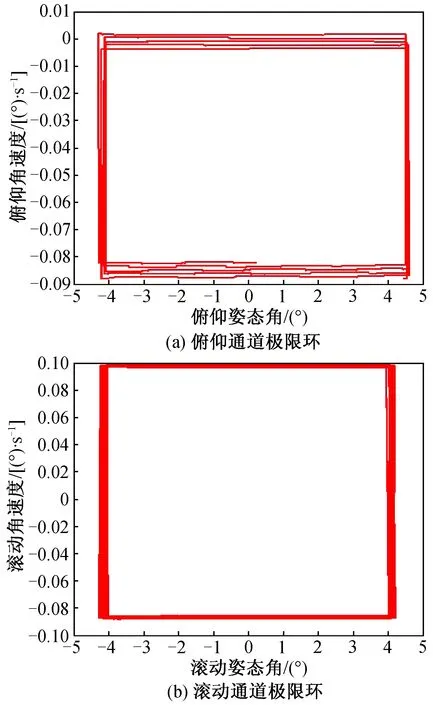
圖7 延遲160 ms補償控制后極限環曲線Fig.7 Limit cycle curve after compensation with time delay of 160 ms

分別對姿控發動機在不同響應延遲時間下，滾動通道采用補償前后的姿態角速度控制精度進行對比分析，結果見表1。由表可見：采用本文基于觀測器的Smith預估控制方案，可有效降低姿控發動機響應延遲對姿態控制精度的影響。當延遲時間為200 ms時，滾動通道控制角速度從0.22 (°)/s減小到0.08 (°)/s。

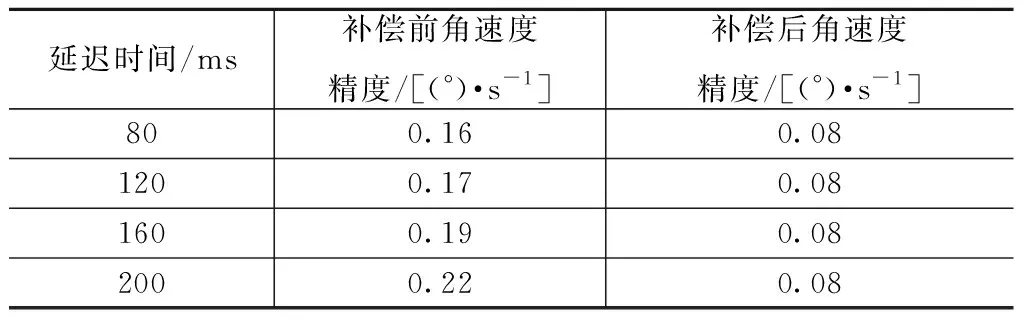
表1 預估補償前后姿態角速度控制精度

5 結束語

本文針對姿控發動機延遲特性引起姿態控制精度降低問題，研究了基于觀測器的Smith預估補償控制方法，結果表明：該方法可有效降低系統延遲對上面級姿態控制精度的影響，顯著提高姿態控制精度，降低姿態控制燃料消耗，為上面級長時間在軌飛行控制提供一定參考。本文方法仍需離線獲取姿控發動機延遲時間，如姿態發動機延遲時間不精確或存在隨機性，則會影響補償控制的精度，因此將開展在線辨識姿控發動機延遲時間方法的研究，以提高系統的自主性。