Hammerstein辨識模型在顫振試飛振動排故中的應用研究

俱利鋒 寇寶智

摘要：本文對顫振機理和非線性氣動彈性主要誘發因素進行了分析，介紹了Hammerstein模型，研究分析了基于Hammerstein模型的某型飛機顫振試飛異常振動排故適用性。試驗過程根據實際的現象特征給出了具體故障排除方法，經地面試驗和飛行試驗結果表明，故障得到了有效排除。所使用的故障診斷和分析方法可以為以后類似問題的解決提供有益的參考和借鑒。

關鍵詞：顫振;飛行試驗;非線性;間隙;Hammerstein模型;辨識

中圖分類號：V217+.39 文獻標識碼：A

顫振是飛機及其部件處于氣流中的一種動不穩定性問題，一旦發生，飛機將在數十秒甚至幾秒鐘內使飛機結構發生毀滅性的破壞。某型飛機是在原型機基礎上進行了重大改進研制的新型飛機，顫振試飛是該型飛機定型試飛的重要科目之一。

非線性氣動彈性問題是顫振飛行試驗中遇到的問題之一。非線性氣動彈性誘發因素有兩個[1]：氣動非線性和結構非線性。在結構非線性方面，飛機與外掛物之間的間隙、操縱面轉軸的間隙、結構相對運動的各種摩擦、復合材料和智能材料的使用，均可能引起剛度非線性和阻尼非線性。

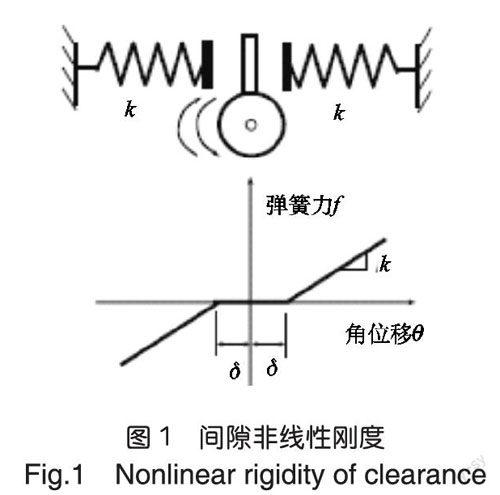
在飛行器機械操縱控制系統中，最常見的非線性問題就是間隙非線性。操縱面鉸鏈以及連接件的安裝間隙是不可避免的，在老化松動等情況下間隙非線性就顯得更為突出。圖1給出結構間隙非線性剛度示意圖，有間隙結構在位移較小的情況下，回復力為零。

許多工程顫振分析的實例表明，結構發生顫振的臨界點附近，常常會有兩個在氣流中的振動模態分支的頻率相互接近的現象，從振動理論的角度看，頻率接近意味著兩個振型的耦合性加強，由此，英國學者Pines提出了一種高度簡化的顫振分析理論—頻率重合理論[2]頻率重合理論對顫振產生的機理解釋為：當飛機的速度增大時，會使飛機結構的某兩個振型分支的頻率發生變化而相互接近，直到這兩個分支的頻率完全相等（即重合），這兩個振型分支的耦合振動就有可能從氣流中吸收能量，從而達到顫振臨界點而發生顫振。圖2給出二維機翼的頻率重合現象。

間隙將導致操縱面的等效操縱剛度降低，直觀上導致某一支結構模態的頻率降低，從而可能引起操縱面顫振。此時最常見的非線性氣彈現象為極限環振蕩，該現象在低于或高于顫振臨界速度的情況都可能出現，而且其隨著速度的增加，振幅會加大。國軍標明確要求如果用操縱面或調整片的操縱系統剛度來防止氣動彈性不穩定性，應確定在飛機使用壽命期內不應超過的間隙限制值。制定本條款的目的是防止大的間隙導致某些結構模態頻率發生變化，使得飛機結構顫振速度變小，增加飛行試驗的風險。鑒于此，在顫振試飛過程異常的結構間隙辨識的準確與否就顯得特別重要。

1 Hammerstein辨識模型

非線性系統參數辨識的困難之一是激勵和響應之間的關系無法事先確定，只能選擇動力學模型來對非線性系統進行描述。如果人為選擇的模型無法近似代替原系統，就可以用非線性黑箱模型進行描述。無論系統的非線性來自哪里，這種模型理論上都可以根據測量數據描述該系統。

對于非線性系統參數模型的辨識問題，最早涉及的是某些特殊類型非線性系統[3]，如Wiener模型、雙線性系統模型、Hammerstein模型等。Hammerstein模型是一類具有特定結構的典型非線性模型，由靜態非線性環節和動態線性環節串聯而成，能較好地反映過程特征，可描述一大類非線性過程。

Hamtrgrstein模型由Narendra和C，aUman于20世紀70年代提出，Hammerstein模型[4～6]是采用輸入端無記憶非線性算子f（·）與線性時不變系統P串聯而形成，如圖3所示。其中f（·）可以取多項式、死區、飽和函數、樣條函數等不同的非線性增益，P可以是狀態空間、傳遞函數或者系統線性基函數。

該模型辨識算法主要分為迭代與非迭代兩種[7，8]。迭代算法在確定非線性算子形式后，對于離散數據辨識，線性部分采用的傳遞函數使用包含移位算子的線性多項式模型表示，迭代目標是使得辨識模型的輸出值與系統測量值之間的誤差最小，最終給出辨識模型的具體參數。

Hammerstein模型在有色噪聲干擾下的差分方程可描述為：

圖3和式（I）中：q^-1為延遲算子;u（t）、w（t）分別為非線性增益環節的輸入和輸出;非線性部分輸出w（t）同時也是線性子系統的輸入：v（t）為線性子系統的輸出;η（t）為噪聲;A（q^-1）、B（R^-1）、C（q^-1）均為延遲算子的多項式，分別如式（2）～式（4）所示;u（t）與η（t）相互獨立。

無記憶非線性增益是區間為[δ₁，δ₂]的死區[9]，表達式為：

設參數矢量為：

參數矢量的估計值為：

辨識非線性Hammerstein模型的目標函數為：式中：s為辨識窗口寬度;y（t）為估計參數模型的輸出值。用式（8）來衡量估計的偏差。

在非線性Hammerstein模型辨識過程中，通過選取一組合適的參數使目標函數達到最小。此時非線性系統辨識問題轉化為參數空間上的極小化問題，可利用優化算法對式（8）求極小值并確定與之對應的模型參數值。

2 某型機顫振試飛異常振動現象

某型機在進行高度H₁、速度V₁的飛行試驗時，發現某左、右平尾對稱位置的振動響應很不對稱（無論使用何種舵面激勵）。以平尾激勵為例，左平尾尖部的振動響應最大到+13.0g，右平尾尖部的振動響應最大到士19.5g。即右平尾的響應幅值約為左平尾響應幅值的1.5倍。而在高度H₁、速度V₂（比V₁小50km/h）時，當使用該平尾進行激勵時，左平尾尖部的振動響應最大到士18.5g，右平尾尖部的振動響應最大到±19.0g，即左、右平尾的響應幅值基本一致。圖4給出高度Hi，速度V，左、右平尾振動響應及頻譜。圖5給出高度Hi，速度V2左、右平尾振動響應及頻譜。圖中的ANC 1和ANC4分別代表左、右平尾尖部傳感器感應的振動響應。

由圖4和圖5可以看出，速度V₁時，左、右平尾振動響應的量值差異較大，而且右平尾振動響應在低頻段和高頻段信號一直信噪比很差。左、右平尾振動響應的頻譜則說明右平尾振動響應中高頻分支的影響較左平尾更明顯一些。而速度V₂時，左、右平尾振動響應的量值差異不大，同時左、右平尾振動響應在低頻段和高頻段信號的信噪比也基本相當。

為了確認異常振動的出現與氣動力因素有無關聯，在地面進行了一次激勵試驗。采用掃頻激勵的方式對左、右平尾進行激勵，在激勵信號相同的情況下，發現其左、右平尾對稱位置的響應差距仍然較大。圖6給出地面試驗左、右平尾振動響應時間歷程和頻譜。由圖6可以看出，左平尾振動響應是右平尾振動響應的1.80倍。可以看出右平尾大響應比左平尾出現的早、結束的早，右邊模態的頻率較左邊小。平尾上其他兩個部位的傳感器數據處理結果也是相同的現象。

圖7給出地面試驗FES激勵左、右平尾舵面偏度時間歷程和頻譜。圖7中的LELESP、RELESP分別代表左、右平尾舵面偏度值。由圖7可以看出，此時左、右平尾舵面開始衰減的頻率，左邊比右邊大1.2Hz。這也可能是由于左邊所能激勵出來的頻率更接近旋轉模態，左邊平尾上的振動響應大于右邊平尾上的振動響應。

3 使用Hammerstein辨識模型對異常現象的分析

為了進一步確認異常振動發生的原因，建立輸入端含有間隙的Hammerstein辨識模型，其中非線性部分使用死區模擬，線性部分采用有兩個模態（一階彎曲、一階旋轉）的線性系統模擬，采用迭代算法分別對地面試驗左、右平尾的響應進行辨識。

由辨識模型的結果可以看出右平尾死區較為明顯，如圖8所示，說明右平尾間隙較大，這也是右平尾響應較小的主要原因。較大間隙可能是長時間使用造成的零部件松動或磨損造成的。圖9則說明辨識給出的線性系統極點分布基本一致，說明系統線性部分模態分布基本一致。

拆下左、右平尾舵機相關結構進行結構檢查，發現左、右平尾舵機作動器上螺栓尺寸均超標，且右平尾螺栓尺寸均超標得更厲害（標準螺栓桿直徑Φ1_-0.028^-0.015mm。實測左Φ14.96mm，右Φ14.95mm），同時作動器三角搖臂上的襯套內部有明顯滑痕，檢查結果與判定結論吻合。

4 Hammerstein辨識模型的排故效果

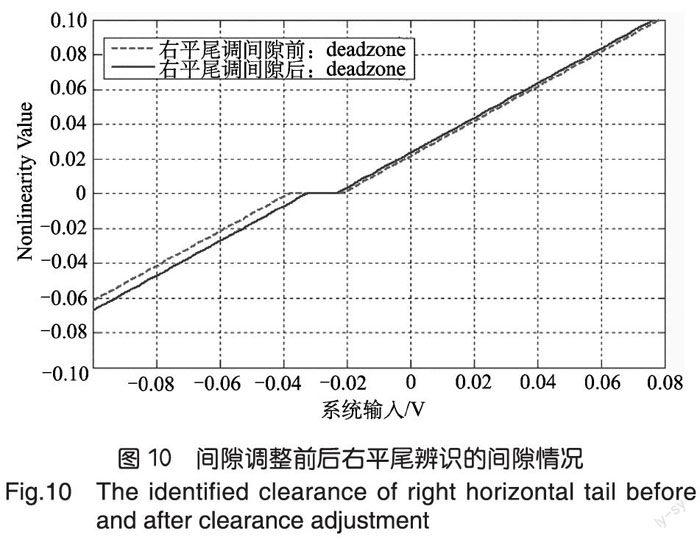
更換了左、右平尾舵機作動器上尺寸超標的螺栓和襯套，又進行了地面激勵試驗，發現調過間隙后死區部分明顯減小，如圖10所示。

5 結論

在某型飛機顫振試飛過程，通過使用Hammerstein模型對全動平尾動力學系統出現的非對稱響應數據進行非線性辨識，確認左、右平尾不對稱響應是因右平尾間隙較大引起的，經檢查左、右平尾相關結構表明，使用Hammerstein模型對全動平尾動力學系統出現的非對稱響應數據進行非線性辨識的結論是正確的。通過使用基于Hammerstein辨識模型進行非線性辨識保障了試飛中異常振動排故指導方針的正確性，進而保障了試驗飛機的安全，加快了試飛的進度，確保了型號的順利定型。該辨識算法可以在后續型號飛行試驗中進一步的應用，為型號試飛的成功提供保障。

參考文獻

[1]俱利鋒，寇寶智.LCO：顫振試飛中一種典型非線性氣彈現象探究[J].強度與環境，2017，44（3）：31-37.

[2]陳桂彬，鄒叢青，楊超.氣動彈性設計基礎[M].北京：北京航空航天大學出版社，2004.

[3]王峰，邢科義，徐小平.辨識Hammerstein模型方法研究[Jl.系統仿真學報，2011，23（6）：1090-1092.

[4]李文江，林思建，王璇.一種辨識Hammerstein模型的新方法[J].計量學報，2015，36（4）：418-422.

[5]翟江濤，赫赤，姚志軍，等.針對Hammerstein模型的典型系統辨識方法[J].江蘇科技大學學報：自然科學版，2016，30（05）：67-71.

[6]胡龍，李建勛.基于Hammerstein的自適應辨識算法及應用[J].控制工程，2013（s1）：186-189.

[7]Juan C G，Enrique B.Subspace identification of multivariableHammerstein and Wiener models[C]//15th Triennial WorldCongress，Barcelona，Spain，2002.

[8]Lacy S L，Bernstein D S.Subspace identification for non-linearsystems with measured-input non-linearites[J].InternationalJournal of Control，2005，78（12）：906-926.

[9]李治濤，韓景龍.間隙非線性氣動彈性系統的辨識[J].航空學報，2012，33（11）：2002-2009.