老齡化背景下儲蓄率與經濟增長關系研究
——基于古典增長模型的分析

賈 非，王士香

(吉林財經大學 統計學院，吉林 長春 130117)

一、引 言

人口老齡化過程將對人類社會產生深刻而持久的影響。我國因老齡化過程中的老齡人口數量多、老齡化速度快、未富先老、城鄉失衡等特征，成為世界上應對人口老齡化任務最重的國家之一。人口老齡化是否將對經濟增長產生嚴重的影響以及政府如何做出相應的政策選擇，已經成為我國老齡化背景下穩定經濟增長以及促進社會發展的重要課題。

關于老齡化過程與經濟增長關系的分析，大多集中于考察人口年齡結構變化和養老支出變化對儲蓄率的影響，并進而考察其對經濟增長的影響。從人口年齡結構角度看，大量文獻聚焦于不斷上升的撫養比對儲蓄率的影響，認為人口總體負擔加重將導致經濟逐漸喪失第一次人口紅利的增長機遇。[1，2]生命周期理論也認為，老齡人口增加將降低社會儲蓄率，并對經濟增長不利。與之相反，較為樂觀的觀點是，撫養比不斷上升的情況下，人們增加預防性儲蓄導致的儲蓄率提高，將帶來老齡化背景下的二次人口紅利。[3]還有觀點認為，老齡化對消費與儲蓄的影響在不同時間與空間上表現出異質性，這意味著二者關系并非為簡單的正向或負向影響關系。[4-6]

從養老支出變化對儲蓄率的影響角度看，相關文獻將其較為系統地歸納為兩種對儲蓄率截然相反的影響機制，即養老保險與儲蓄相互替代的“資產替代效應”和養老保險對提前退休的吸引力導致退休前增加預防儲蓄的“引致退休效應”。[7，8]在實證分析中，相關文獻也未取得一致結論。一些文獻認為，養老支出對儲蓄率的影響取決于養老保險的制度，還有文獻得出養老保險對儲蓄率影響并不顯著的結論。[9-11]綜上，關于老齡化背景下儲蓄率變化的研究很難取得具有一致性規律的結論，但老齡化過程中儲蓄率的變化將對經濟增長起到重要影響已成為不爭的事實。與以往研究不同，本文的目的是將儲蓄率看作老齡化過程的外生影響變量，考察儲蓄率對老齡化背景下經濟增長的影響。選擇這一研究視角的原因如下：其一，老齡化并非僅通過影響儲蓄率的路徑對經濟產生影響，其對經濟增長的影響具有多種機制。譬如，老齡化將導致生產要素收益發生顯著變化，并對生產能力產生潛在影響[12，13]；人口老齡化催生了消費性服務業的迅速發展，對產業結構優化升級具有明顯影響[14]；老齡化過程中增加的養老支出還可能通過擠占政府購買性支出，抑制經濟增長。其二，儲蓄率是經濟、金融、貿易關系中的重要變量，其變化受到多種因素的影響。根據以往文獻，除了人口結構和社會保障外，儲蓄率還在很大程度上受到實際利率、外部貿易、收入增長、信用發展、房產價格等因素的影響。[15]而我國儲蓄率居高不下的主要影響因素是家庭收入和房產價格。[16]這表明，儲蓄率的波動絕大部分是外生于老齡化過程的。因此，本文試圖簡化儲蓄率在老齡化進程中發生的復雜變化，將儲蓄率看作外生于老齡化過程的經濟變量，并考察老齡化過程中，老齡化程度、養老支出對經濟增長的影響如何取決于儲蓄率的變化。從這一角度看，本文的分析豐富了老齡化背景下儲蓄率與經濟增長關系的理論，從而擴展了老齡化相關研究的理論邊界。

二、理論模型與假設

新古典經濟增長模型幾乎是所有增長問題研究的出發點。該模型主要包含產出 (Y)、資本 (K)、勞動 (L) 和技術進步 (A) 四個變量，技術進步進入模型的方式主要有三種類型：哈羅德中性、索洛中性和希克斯中性。本文主要考慮哈羅德中性即勞動加強型的經濟增長模型，此時生產函數的形式為：

Y=F(K,AL)

假定規模報酬不變，定義k=K/AL，y=Y/AL，分別表示每單位有效勞動的平均資本和每單位有效勞動的平均產出，則生產函數可寫成如下集約形式：y=F(k,1)，定義f(k)=F(k,1)，則y=f(k)，該式滿足f(0)=0，f′(k)>0，f″(k)<0以及稻田條件。

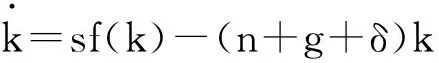
(1)

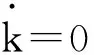
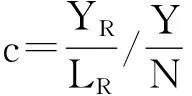
(2)

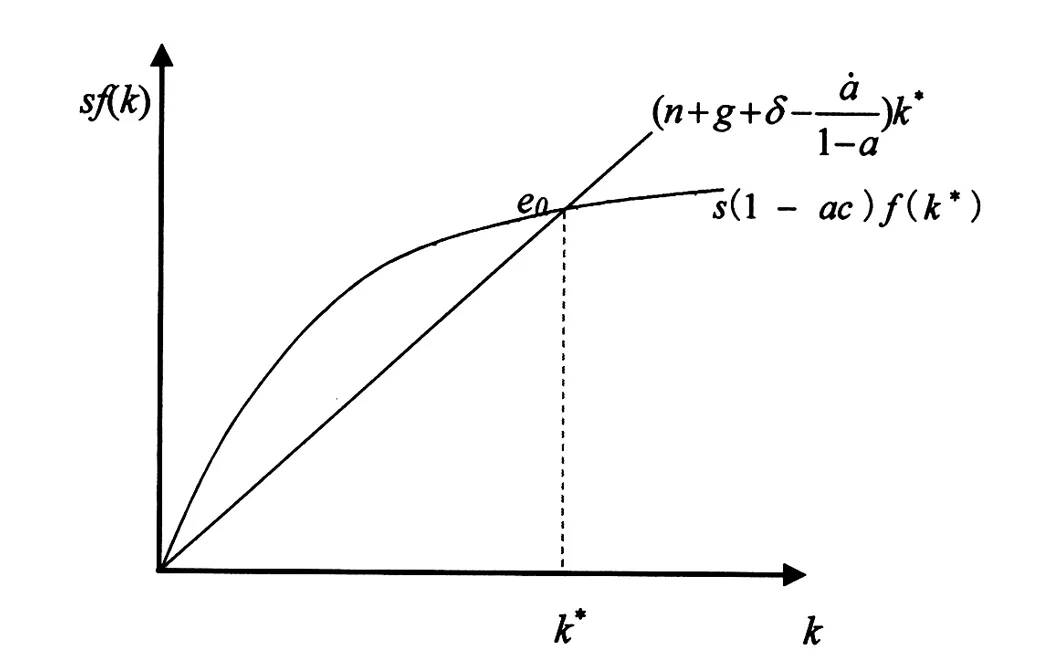
圖1 老齡化背景下經濟平衡增長路徑

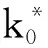
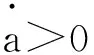
假設1：老齡化程度 (a) 加深對平衡增長路徑下人均產出 (y) 的影響取決于儲蓄率 (s) 的高低，較高的儲蓄率將強化人口老齡化對人均產出的負向影響。

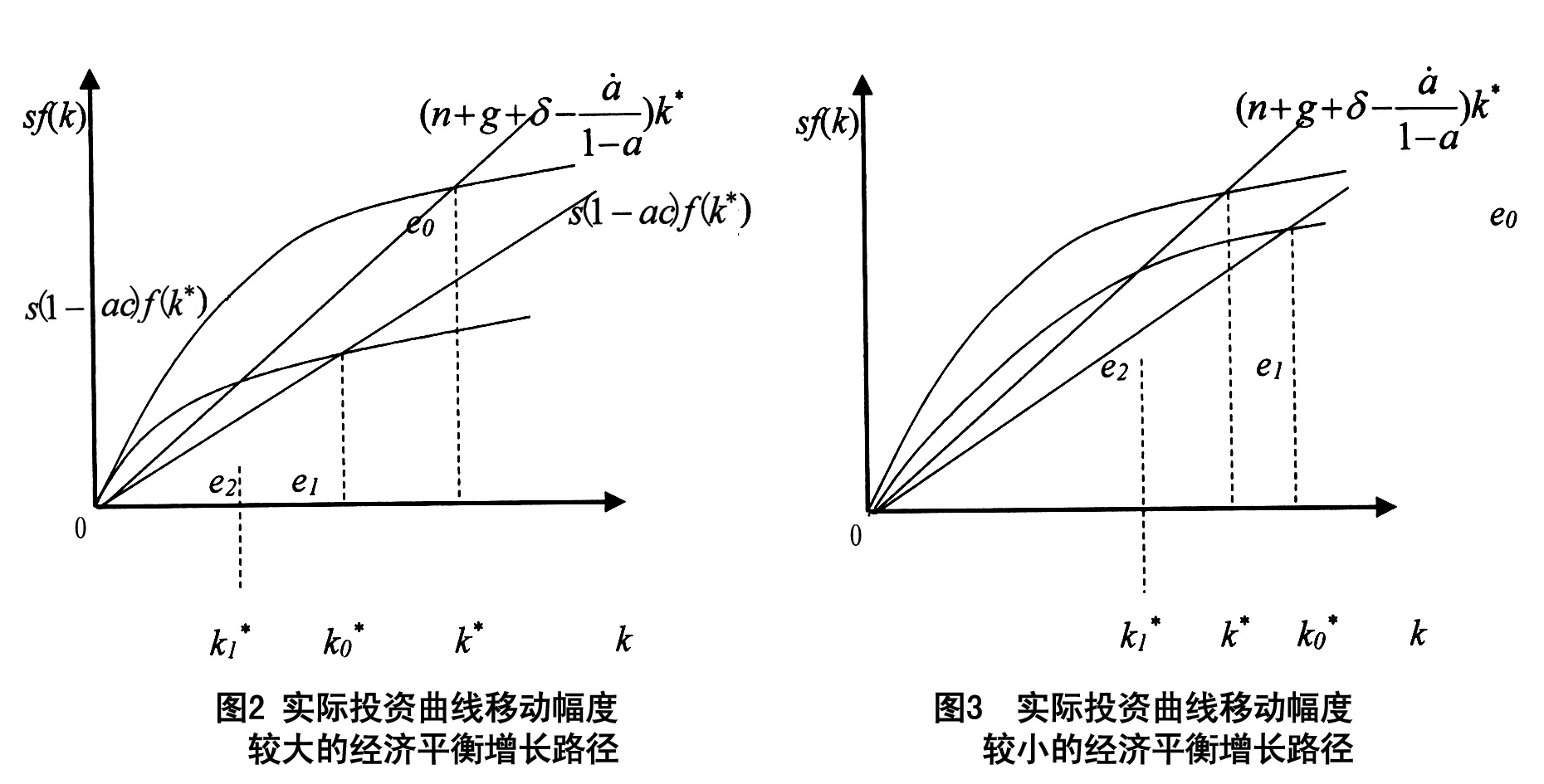
假設2：養老水平增加 (c變大) 對平衡增長路徑下的人均產出 (y) 具有負向影響。

假設3：儲蓄率(s)越高，養老水平對人均產出(y)的負向影響越強；反之，儲蓄率(s)越低，養老水平對人均產出(y)的負向影響越弱。

三、樣本、變量與研究方法

(一) 樣本與變量

本文選擇我國31個省 (市、自治區) 作為樣本進行研究，樣本區間為2005～2016年，所有數據的來源為wind資訊金融終端宏觀數據庫。本文的實證分析包含如下變量：

被解釋變量：實體經濟增長 (y) ，用人均產出表示，由各省生產總值 (GDP) 與總人口之比計算得出，單位為萬元/人。

解釋變量：老齡化程度(a)，用老年人口比表示，由各省市歷年60歲以上人口抽樣數與全部人口抽樣數做商得到。[注]由于缺失2010年各省市的人口抽樣調查數據，因此2010年老年人口比數據無法得到，本文使用平均數公式，運用插值法進行補齊。養老水平(c)，用老年人人均養老保險額度(養老保險支出與60歲以上人口數之比)除以人均收入(生產總值與總人口之比) 得出，該變量表示相對全社會人均收入，老年人口的人均收入水平。儲蓄率 (s)，在假設儲蓄全部轉化為投資的前提下，儲蓄率近似與資本形成率相等，因此，文中儲蓄率由各省市歷年資本形成總額占總產值的比例表示。

控制變量：少兒撫養比 (ccr)，由各省市歷年0～14歲人口抽樣數與全部人口抽樣數做商得到；財政支出 (fex)，由各省地方人均公共財政支出表示，單位為萬元/人；凈出口 (nex)，由各省出口總額與進口總額的差與該省總人口做商得到，單位為萬元/人。

表1中給出上述變量的描述性統計分析與相關系數矩陣。可以看出各個解釋變量之間相關系數均處于0.5以下，說明變量之間沒有明顯的多重共線性問題。盡管如此，我們依然計算了方差膨脹因子，結果顯示VIF值處于2.46以下，遠低于臨界值10，進一步證明了變量之間不存在明顯的多重共線性問題。

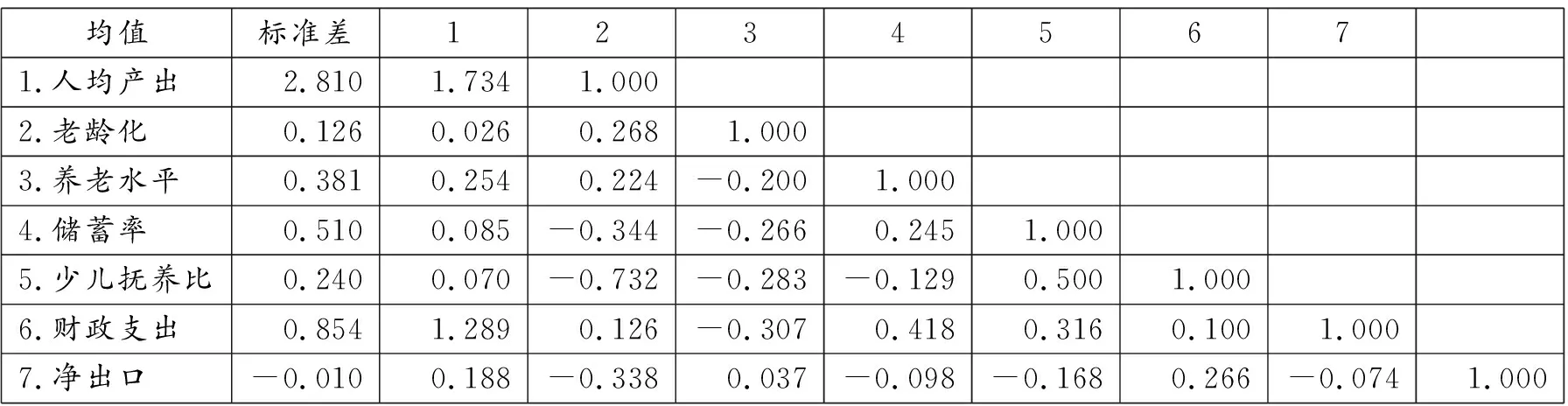
表1 變量描述性統計與相關系數矩陣

為了保證模型的穩定性，在實證分析之前對各變量進行平穩性檢驗。為確保檢驗結果的穩健性，選擇IPS方法和LLC進行檢驗。盡管相對于允許個體單位根過程和異構參數的IPS檢驗而言，LLC檢驗假設參數具有同質性可能導致檢驗結果存在異質性偏差，但LLC檢驗仍然可以作為補充，驗證IPS檢驗結果的穩健性。檢驗結果見表2。可以看出，ccr變量的IPS檢驗結果是非平穩的，但LLC檢驗的結果是在95%的置信度下平穩的，所有其它變量IPS檢驗都是平穩的。因此，可以認為所有變量均通過平穩性檢驗。

表2 變量單位根檢驗

注： *、**、***分別表示該統計量在10%、5%和1%顯著水平上顯著。

(二) 研究方法

宏觀經濟變量之間通常存在理論上的相互因果關系，在本文構建的模型中，經濟增長變量可能通過影響人口壽命而影響老齡化程度，同時也能夠對養老水平和儲蓄率產生影響，因此，解釋變量具有理論上的內生性問題。為此，本文使用面板平滑轉移模型 (PSTR模型) 進行參數估計，因為該模型能夠有效限制因解釋變量內生性導致的估計偏差。[17]盡管如此，為控制內生解釋變量問題，本文仍在模型中將全部的解釋變量和控制變量滯后一期，因為經濟增長很難對上一期的老齡化程度、養老水平和儲蓄率產生影響。

本文的實證分析中采用的PSTR模型是一個包含外生變量的固定效應面板回歸模型，其系數可隨時間和個體的變化而發生變化。[18]PSTR模型是平滑轉移回歸 (STR) 模型的拓展，是為個體和時間上存在異質性的面板數據進行建模使用的。該模型假設參數是一個可觀測變量的有界連續函數，并允許回歸系數之間存在異質性。包含兩個區制和一個轉移函數的簡單PSTR模型可以被定義為：

(3)

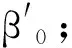
式(3)中xit對yit的影響可以表示為：

(4)

其中，轉換函數g(qit;γ,c)是可觀測變量qit的連續函數，轉換函數經過標準化后介于0和1之間。我們考慮如下邏輯轉換方程：

(5)

其中，c=(c1,…,cm)′是一個m維的位置參數向量，式中參數滿足γ>0且c1≤ c2≤ …≤cm。

包含多個轉移函數的PSTR模型可表示為：

(6)

若對于所有的j=1,…,r，都有γj→∞，轉移函數轉變為一個示性函數I(A)，式(6)就變成一個包含r + 1個區制的PTR模型。因此，多層次PSTR模型可視為多區制PTR模型的一般化過程。

模型估計過程如下：首先，進行模型的線性和剩余非線性檢驗，如果拒絕了模型不存在非線性的原假設，則表明樣本數據可以使用PSTR模型進行建模，否則應使用傳統面板固定效應模型建模。其次，對模型轉換方程的個數進行檢驗，這一步驟將對不斷增加轉換函數個數進行假設檢驗，直至模型不再含有剩余的非線性部分，即確定轉換函數的個數。最后，對模型的參數進行估計，運用非線性最小二乘法 (NLS) 進行面板參數估計，確定轉換參數、位置參數、固定效應影響系數和轉換函數影響系數。

四、實證結果

(一) 非線性檢驗與轉換方程的個數確定

非線性檢驗的原假設與備擇假設是H0: r = 0，H1: r = 1，假設檢驗的統計量為LM統計量和LMF統計量。根據表3的結果可知，無論在m = 1還是m = 2的情況下，模型均能夠在5%的顯著水平下拒絕r = 0的原假設，這意味著解釋變量與被解釋變量之間存在非線性關系。剩余非線性檢驗的原假設與備擇假設分別是H0: r = 1，H1: r = 2，根據表3中統計量LM和LMF的計算結果可知，無論在m = 1還是m = 2的情況下，模型均接受了r = 1的原假設，說明模型均存在一個轉移函數。進一步，根據AIC和BIC值的比較可知，模型在m = 1時表現最佳。為此可以得出結論：模型均為具有1個轉換函數1個位置變量的PSTR模型。

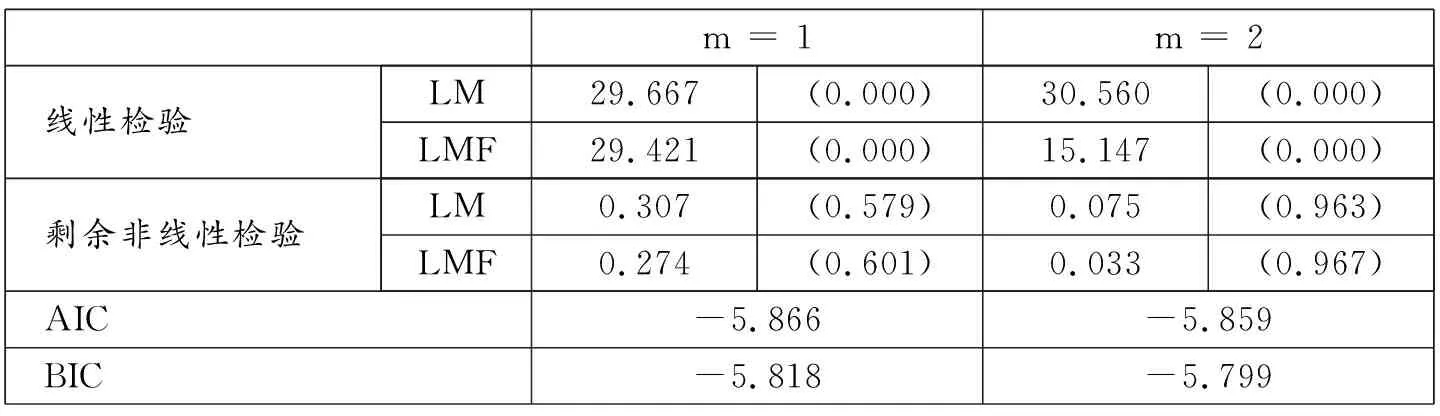
表3 線性和剩余非線性檢驗結果

(二) PSTR模型估計結果

表4中給出了模型的參數估計結果。模型1的門限變量為儲蓄率，其位置參數值為0.501，說明當儲蓄率處于0.501兩側時，各變量對人均產出的影響明顯不同，但這種變化是平滑轉換的，其平滑參數值為8.386，意味著平滑轉換的速度較快。根據回歸參數可知，在位置參數兩側，老齡化水平和養老水平對人均產出的影響均在1%的顯著水平下顯著。當儲蓄率為0.501時，老齡化水平 (a) 對人均產出 (y) 的影響系數為-0.305；當儲蓄率小于0.501時，這一影響系數大于-0.305，隨著儲蓄率逐漸變小，其影響系數最終穩定于-0.063；當儲蓄率大于0.501時，該影響系數小于-0.305，隨著儲蓄率逐漸變大，其影響系數最終穩定于-0.548。這一結果表明，隨著儲蓄率增大，老齡化水平 (a) 對人均產出 (y) 的負向影響增強，該結果支持假設1。同理，當儲蓄率為0.501時，養老水平 (c) 對人均產出 (y) 的影響系數為-4.324；當儲蓄率小于0.501時，這一影響系數變大，并隨著儲蓄率逐漸變小，其影響系數最終穩定于-1.208；當儲蓄率大于0.501時，該影響系數變小，隨著儲蓄率逐漸變大，其影響系數最終穩定于-7.440。該結果意味著，儲蓄率增大過程中，老齡化水平 (a) 對人均產出 (y) 的負向影響增強，該結果支持假設3。養老水平對人均產出的影響始終為負數，這表明養老水平增加始終對人均產出具有負向影響，這一結論支持假設2。因此，PSTR模型的估計結果支持了所有的理論假設。

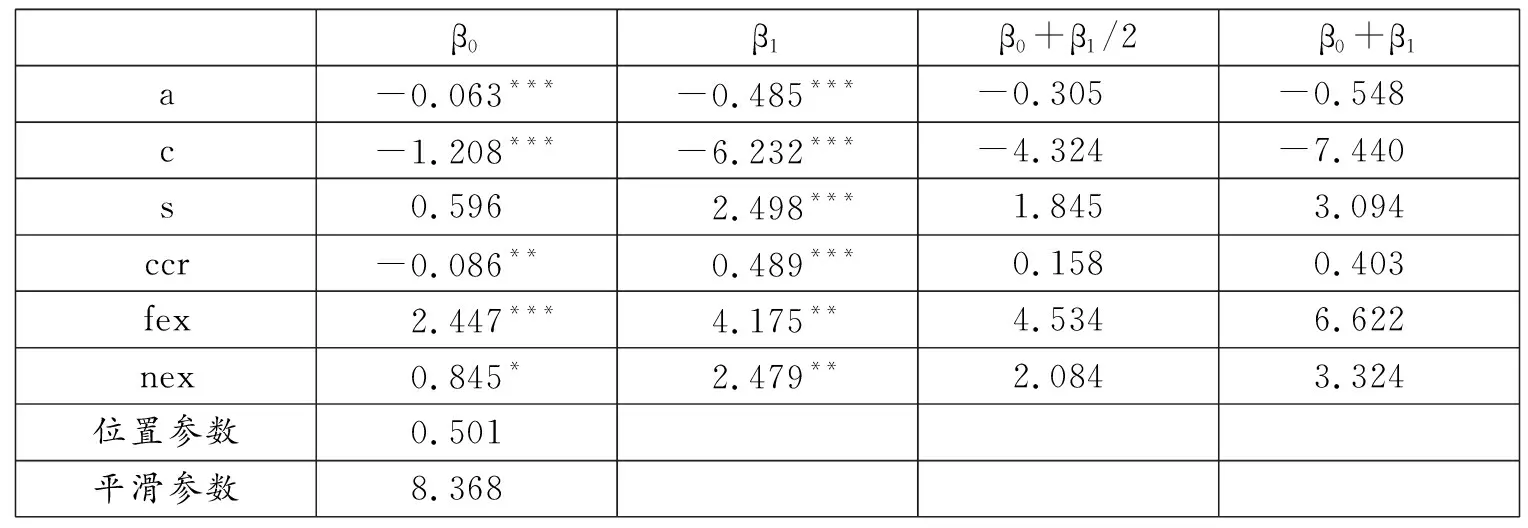
表4 PSTR模型參數估計結果

注：*、**、***分別表示在10%、5%和1%顯著水平上顯著。

五、結論與啟示

關于老齡化、養老支出與經濟增長關系的研究，以往文獻通常聚焦于儲蓄率的中介作用，即老齡化、養老支出如何影響儲蓄率并進而對經濟增長產生影響。與以往研究不同，本文假設儲蓄率外生于老齡化過程，并以這一假設為前提，在新古典經濟增長模型中加入了老齡化的經濟要素，推導了老齡化背景下的經濟增長模型。根據模型給出的理論啟示，本文運用限制了解釋變量內生影響的PSTR模型，驗證了儲蓄率的變化在老齡化和養老支出對經濟增長產生影響過程中的作用。實證分析結果顯示，老齡化和養老支出對經濟增長的影響程度取決于儲蓄率的高低。具體而言，儲蓄率越高，老齡化和養老支出對經濟增長的負向影響越大，這意味著，對于儲蓄率較高的地區，宏觀政策應格外關注老齡化帶來的經濟負效應。本文的理論與實證分析，揭示了儲蓄率在老齡化背景下對經濟增長影響的新機制，從而豐富了以往關于儲蓄率與經濟增長關系的理論。