基于多元回歸方法的巖石物理性質預測模型研究*
陳小根 武立岐
(北京科技大學土木與資源工程學院)
為了在巖石中設計結構,鉆孔作業是必不可少的環節。通過鉆孔了解地層地質情況,對工程設計有指導意義,同時用于礦區巖石開挖工程所需的爆破炮孔也要通過鉆孔作業完成,鉆孔作業費用在工程預算中占較大的比重。所以,在鉆孔作業之前,一般需要清楚巖石的完整性質,比如所鉆地層巖石強度、密度等參數,從而確定施工技術和施工方案。獲取巖石性質的傳統方式是取芯,由實驗測定。由于直接法耗費比較大,還有局限性,所以對巖石性質預測的間接法引起了一些學者[1-3]的興趣。間接法不僅可用于確定完整的巖石性質,而且可以用于檢驗試驗結果。
許多研究人員已經間接地定義各種巖石的性質采用不同的方法確定[4-8]。Kahraman等[9-11]研究在鉆進過程中巖石的聲的識別,利用傅立葉變換在旋轉鉆進過程中獲得的聲波信號控制巖石破碎過程。Vardhan等[12-13]在實驗室通過改變鉆頭施加的推力和抗壓強度,嘗試用聲級的變化確定巖體性質。通過科學方法將鉆進參數和巖石物理性質建立起聯系,對于巖石鉆進工程優化、機械選擇、耗損降低、工作效率提高都有重要意義。
本文通過室內鉆進實驗數據,利用多元回歸的方法,建立鉆進參數與巖石物理性質的數學模型,用于巖石物理性質的預測,并對模型進行驗證。
1 巖石物理性質分析
巖石單軸抗壓強度σ是經常使用的力學參數,是指試樣只在一個方向受壓時所得的極限粉碎強度,也就是說將巖石試樣放在壓力機的上下壓板之間進行加壓,直至試樣被壓壞時測得的壓力強度值。一般利用單軸抗壓強度儀器來測定。
縱波在巖石中傳播的速度VP是地球物理勘探中常用的參數,它通常使用在現場和實驗室來表征和確定巖石的動力性質。縱波速度可以在實驗室中直接或間接測量。
巖石的密度ρ與巖石組成礦物及巖石的結構有關[14]。按巖石含水狀態分為巖石天然密度和干密度。巖石密度對組成特定巖石類型的礦物非常敏感。一般用直接測量方法得出巖樣的體積v,稱出原巖樣烘干質量m,然后求出巖石密度。
本次研究的目的是找出3個表征巖石性質的物理力學參數(σ,VP和ρ)和鉆進過程中產生的聲級水平之間的關系,建立估算模型,輸入間接參數,預估出巖石的性質。
2 實驗研究
2.1 實驗的巖石樣品
從現場獲得的10種不同巖石樣本包括板巖、石英巖、淺綠色石英巖、石榴石黑云巖、粉石英巖、綠石英巖、榴輝巖、黃色石英巖、煙熏石英巖、大理石。巖塊尺寸為20 cm×20 cm×20 cm。
2.2 實驗裝置
在實驗室采用BMV45 T20型計算機數控(CNC)垂直加工中心(圖1)進行巖石樣品鉆進實驗。用于鉆進作業的刀柄長40 mm,硬質合金鉆頭直徑為6,10,16和20 mm,鉆孔長30 mm。由于鉆進方法會影響產生的聲音,在整個鉆進過程中,為了獲得一致的數據,提供相對恒定的轉速和穿透率。

圖1 CNC垂直加工中心
2.3 A計權等效聲級測定
在鉆孔過程中,為了克服巖塊的振動,用虎鉗夾將巖石樣品緊緊地固定在機器的臺面上。
鉆頭直徑為6,10,16和20 mm;鉆頭轉速為150,200,250和300 r/min;鉆速為2,3,4和5 mm/min。對于不同鉆頭直徑、鉆頭轉速和鉆速的組合,總共得到64組試驗條件,記錄巖塊64種不同的A計權等效連續聲級(Leq)。對于所有的測量,聲級計保持在距離鉆頭1.5 cm。對于一個特定的條件、同一塊巖石,在相對快速的演替中,確定5次聲級水平。結果發現,記錄的等效聲級幾乎一致。5次測量算術平均作為計算一個特定條件的A計權等效聲級值。
3 基于鉆進過程聲級的巖石參數預測
3.1 巖石參數及聲級
從實驗室測試和基本的統計評估,如均值、最大值、最小值的結果以及不同參數的標準偏差,隨著范圍(最大值和最小值)的A計權等效聲級在鉆井過程中完整的變質巖石記錄見表1。對這些結果采用多元回歸分析和方差分析(ANOVA)。巖石性質(σ,VP和ρ)與鉆進過程的聲級的關系見圖2。
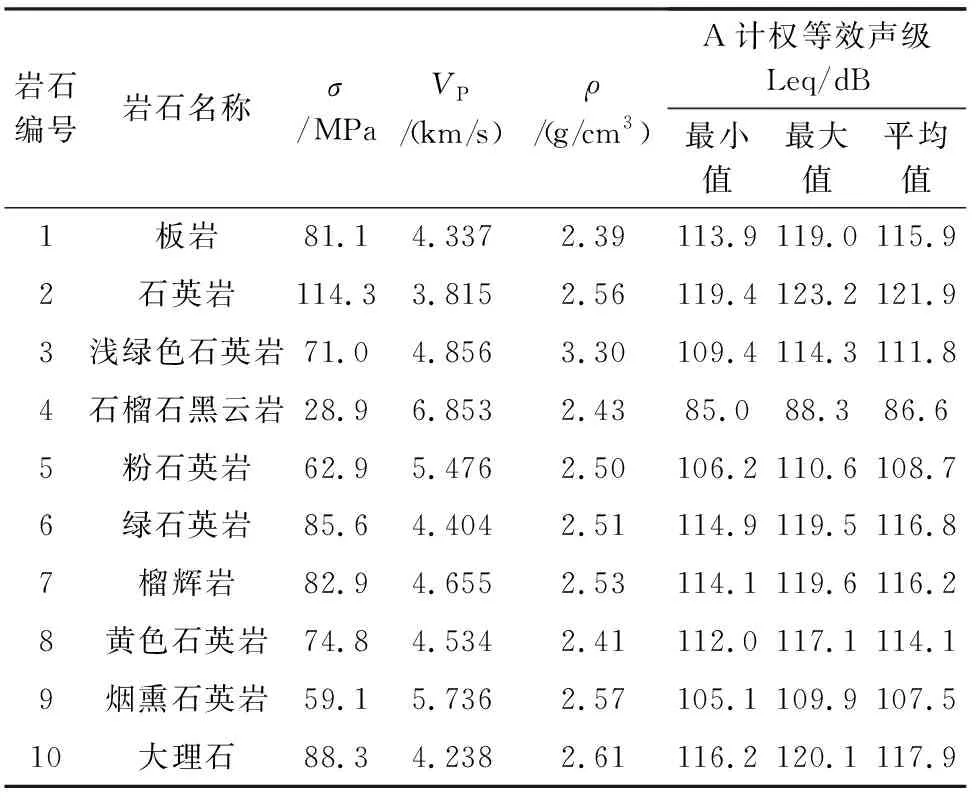
表1 巖石物理力學參數
從實驗數據可以看出,巖石在不同工況下的等效聲級與表征巖石特性的物理參數(σ,VP和ρ)之間表現出了良好的相關性。
3.2 基于聲級的巖石參數預測模型
為了獲得合適且實用的預測定性關系,需要對巖石物理力學性質和鉆進過程變量參數進行建模。一個詳細的過程表示可以預期一個二階模型,通過在響應和相應的重要參數之間使用非線性擬合,采用多元回歸方法對各種響應進行建模。模型的性能取決于以復雜方式起作用和相互作用的大量因素。
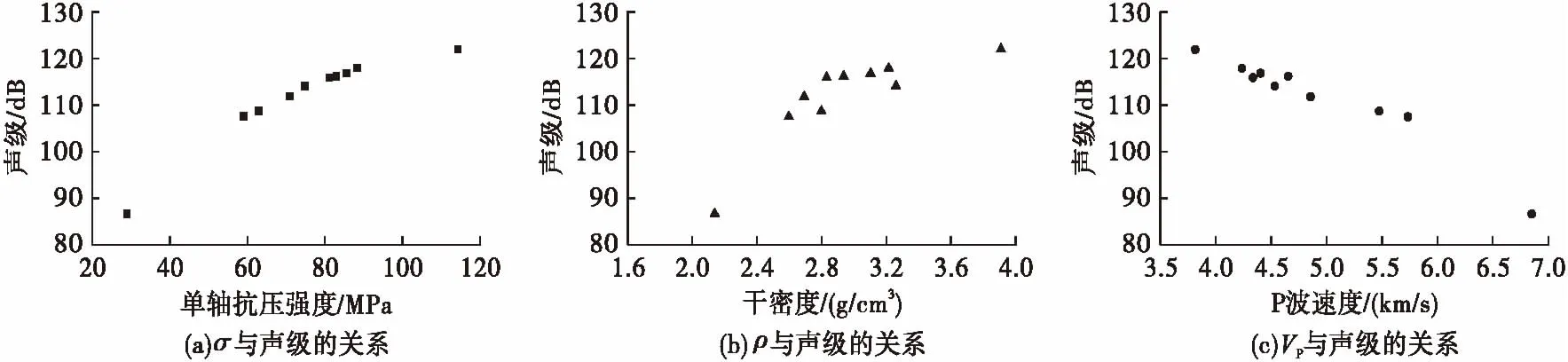
圖2 巖石性質與聲級的關系
鉆進過程中產生的聲級水平也受多種因素的影響,方差分析發現輸入參數對期望響應有顯著影響。為了便于實驗和測量,本次研究除了考慮在鉆進過程中產生的等效聲級A(dB),還考慮3個重要因素,即鉆頭直徑B(mm)、鉆頭轉速C(r/min)、鉆進速率D(mm/min)。對應所考慮的響應是單軸抗壓強度σ、P波速度VP和干密度ρ。所考慮的物理力學性質參數的數學模型可以表示為
Y=f(x1,x2,x3,…,xn)+∈ ,
(1)
式中,Y為響應;x1,x2,x3,…,xn為獨立變量;∈為擬合誤差;f的二次模型可以表示為
(2)
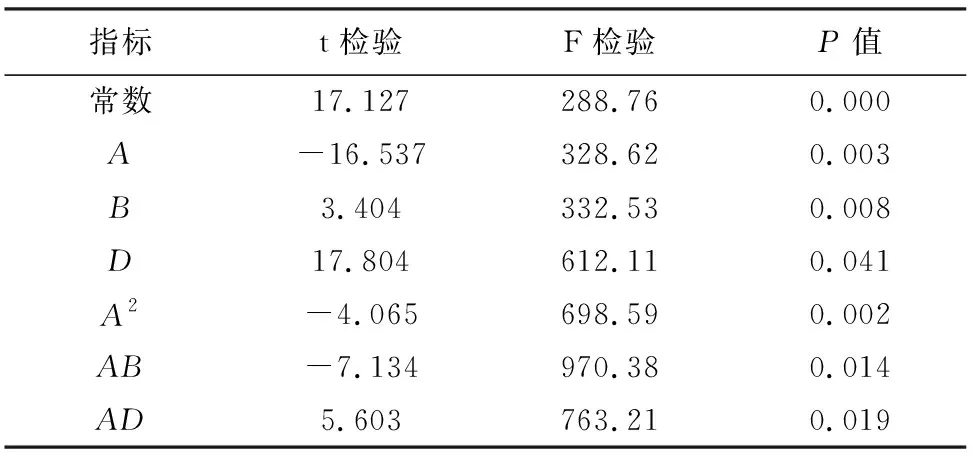
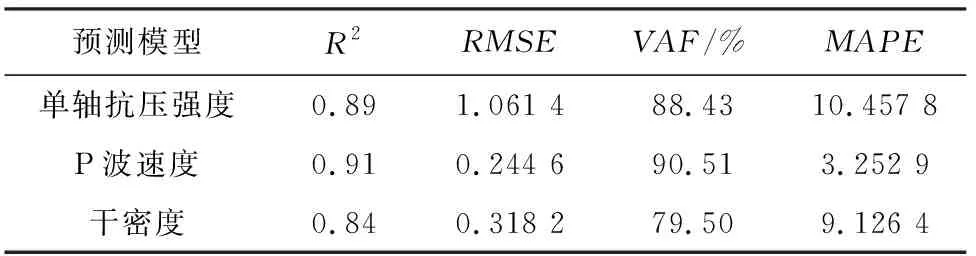
式中,ai為xi的線性效應;aij為xi的二次效應,aij(i 模型里響應面包含常數項、線性項、平方項和交叉乘積項。為了比較所有合理的回歸模型,采用一種向后淘汰程序篩選。首先建立回歸方程,然后對回歸方程系數進行a水平(“經驗法則”是將a設置為0.05,即95%置信區間)的t檢驗,如果t統計量在選定的a水平不顯著,考慮的獨立變量從模型中被刪除,并且通過使用包含所有剩余獨立變量的回歸模型來執行回歸分析;如果t統計量顯著,則選擇模型。通過選擇具有絕對最小t統計量的自變量得到需要的回歸方程,并對方程進行F檢驗,最后建立預測巖石特性物理力學參數的回歸模型。 3.2.1 單軸抗壓強度σ 單軸抗壓強度σ最終建立的回歸模型為 σ=543.142-12.080×A+1.876×B+0.065× C+0.071×A2-0.017×A×B-0.001×A×C. (3) 估算單軸抗壓強度的回歸模型的檢驗分析見表2。對于σ,獨立變量A、B和C的P值都小于0.05,具有統計學意義。除此之外,A2的P值以及B、C與A有關的交互項AB和AC的P值都小于0.05,從而建立了實驗結果。 表2 σ估計的回歸模型檢驗分析 將自變量代入到回歸模型中,得到單軸抗壓強度的預測值,在同一個圖中繪制出預測值與實測值,見圖3。 圖3 單軸抗壓強度預測值與實測值●—預測值;■—實測值 3.2.2 P波速度VP P波速度回歸模型為 VP=-1.192 6+0.223 6×A-0.025 56×B- 0.001 3×B2-0.014×A2+0.000 56×A×B. (4) 估算P波速度的回歸模型的檢驗分析見表3。對于VP,獨立變量A、B的P值都小于0.05,具有統計學意義。除此之外,A2、B2的P值以及B與A有關的交互項AB的P值都小于0.05,從而建立了實驗結果。 表3 P波速度估計的回歸模型系數分析 將自變量代入到回歸模型中,得到P波速度的預測值,在同一個圖中繪制出預測值與實測值,見圖4。 圖4 P波速度預測值與實測值●—預測值;■—實測值 3.2.3 干密度ρ 干密度ρ最終模型為 ρ=19.336-0.392 4×A+0.074 7×B+ 0.063 6×D+0.002 2×A2-0.000 8× A×B-0.000 56×A×D. (5) 估算干密度的回歸模型的檢驗分析見表4。對于ρ,獨立變量A、B、D的P值都小于0.05,具有統計學意義。除此之外,A2的P值以及B、D與A有關的交互項AB和AD的P值都小于0.05,從而建立了實驗結果。 表4 干密度估計的回歸模型系數分析 將自變量代入到回歸模型中,得到干密度的預測值,在同一個圖中繪制出預測值與實測值,見圖5。 圖5 干密度預測值與實驗值●—預測值;■—實測值 測量值與預測值之間的相關系數是檢驗模型預測性能的一個很好的指標。在本研究中,數值計算(VAF)和均方根誤差(RMSE)指數是為了控制在研究中開發的預測模型預測能力的表現。 (6) (7) 式中,y和y′分別為測量值和預測值。 對于一個模型,若VAF為100,且RMSE為0,則該模型是優良的。平均絕對百分比誤差(MAPE)是統計中擬合系列值精確度的測量值,也被用作模型的預測性能。MAPE通常以百分比表示準確性。 (8) 式中,Ai為實際值;Pi為預測值。 建立的回歸模型的性能指標見表5。 表5 回歸模型的性能指標 由表5可知,與單軸抗壓強度和干密度模型相比,所開發的預測P波速度的模型更有效,其具有低的RMSE值和高的VAF值。這些值可用于將已開發模型的性能與其他間接調查進行比較。對于單軸抗壓強度、P波速度、干密度,MAPE值分別為10.457 8,3.252 9,9.126 4,即模型的準確度分別為89.5%,96.7%,90.8%,這間接地說明了預測模型的可靠性。 在考慮鉆頭直徑、鉆頭轉速和鉆進速度的影響下,研究及評價在鉆井過程中產生的3個完整巖石特性和聲級之間的經驗關系。所開發的預測模型并不旨在替代ISRM建議的測試方法,而是作為一種快速而簡單的方法來估計完整巖石的物理力學性質,其優點之一是可以通過一個實驗來估計多個巖石性質。回歸模型計算出的巖石特性值和實際值比較接近,表明所開發的模型可以得到有效應用,具有可接受的精度,在設計的初步階段可以預測采礦行業的完整巖石性質。然而,需要進一步的研究來預測巖體的性質。
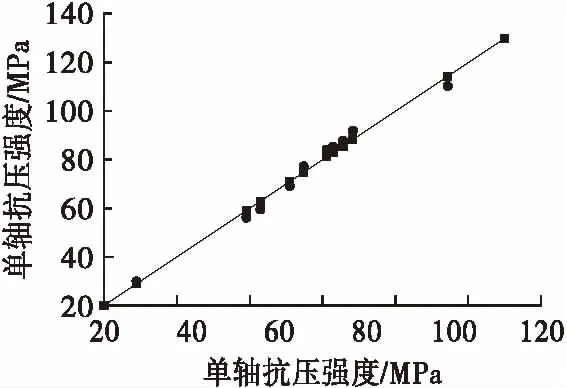

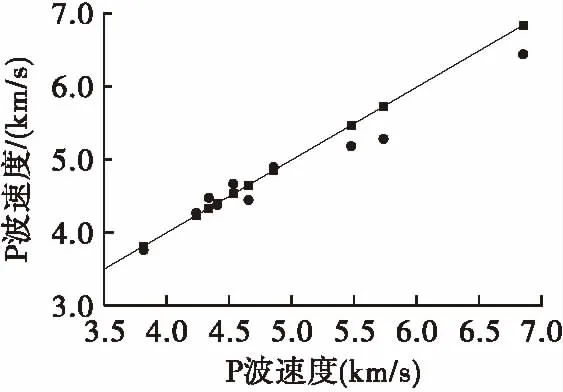

3.3 模型的預測性能
4 結 論

