一種改良的主動頻率偏移孤島檢測方法

林 義，何通能

(浙江工業大學信息學院電子信息與智能系統研究所，杭州 310023)

0 引言

隨著工業化的發展，全球范圍內的能源緊缺已經變成阻礙社會可持續發展的嚴重問題。特別是廣泛使用的化石燃料的不可再生性以及對環境的污染程度，迫使發展新能源成為當前迫在眉睫的任務。光伏發電［1］因其設備安裝簡單、規模靈活、維護簡單、無污染等優勢展示出其寬廣的應用前景。隨著分布式光伏系統規模不斷擴大，為了使電網系統能夠安全運行，孤島檢測成為研究光伏并網的核心問題，各種不同的孤島檢測算法［2-4］被陸續提出。

在光伏發電系統正常工作情況下，若公共電網突然不再繼續向本地負載供電，而光伏發電系統仍然進行工作，導致本地負載處于局部供電的情況，形成一個獨立的供電系統，則稱此狀態為孤島現象。在并網系統中，孤島現象包括非計劃性孤島現象與計劃性孤島現象。其中，非計劃性孤島現象是指非計劃、不受控地發生孤島現象;計劃性孤島現象是按照事先選擇的控制策略，人為地發生孤島現象。非計劃性孤島現象會對系統設備帶來非常大的危害，例如會造成用戶的設備損壞、發電系統的燒毀，同時也對電網的供電品質產生影響，使得電網的安全性大大地降低，那么必須要抑制非計劃性孤島現象的產生。因此，如何準確、快速地檢測出孤島現象［5］對整個并網系統可靠運行有著十分重要的意義。

1 孤島檢測的傳統方法

當前孤島檢測方式包含兩種:被動檢測法和主動檢測法。被動檢測法主要是通過檢測公共耦合點PCC(Point of Common Coupling)的電壓幅值、相位以及頻率等參數變化作為判斷電網是否發生斷電的依據，例如通過遠程通信方法來檢測PCC點斷路器是否發生跳閘來判斷孤島等。這種方法通常檢測周期長且存在比較大的檢測盲區NDZ(nondetection zone)，NDZ是判斷該孤島檢測方法是否高效的標準;主動檢測法是通過主動加入擾動的正反饋信號到并網逆變器中，使得逆變器的輸出電壓幅值、相位、頻率等參數產生一定的波動。在電網正常工作時，這些擾動信號不會促使并網逆變器的輸出特性發生改變;在電網發生故障時，因為主動加入擾動的信號存在正反饋作用，這使得并網逆變器的輸出特性能夠迅速累加且超過閥值從而被檢測到。

主動檢測法的優點是檢測盲區較小、檢測精度高，但是主動加入的擾動信號會對電能質量產生一定的影響。主動檢測法主要包括有滑模頻率偏移法SMS(slip－mode frequency shift)［6］、無功功率補償法、主動頻率偏移法 AFD(Active Frequency Drift)和頻率跳變法［7］等。其中AFD是比較常用的主動檢測法。它的特點是檢出率較高、檢測速度較快。但是當逆變器輸出功率與負載功率平衡或者不平衡程度較小時，難以檢測出孤島且輸出電流含有較大的諧波。為了能夠在這種情況下檢測出孤島效應，提出了許多改進的AFD檢測方法［8-10］，大部分方法基本都是對減少檢測盲區和系統所增加的擾動量之間進行決擇。本文提出一種改良的主動頻率偏移孤島檢測算法，該方法能夠較大的減少檢測盲區，降低電流的諧波含量，從而提高了整個光伏發電系統的可靠性［11-12］。

2 AFD法的基本原理及其參數

2.1 AFD法的基本原理

主動頻率偏移法 (AFD)是一種常用的主動式檢測方法，該方法通過對逆變器輸出電流注入擾動信號，當發生孤島狀態時，使得頻率發生偏移超出設定閥值，從而檢測出孤島狀態。通常電網電壓和輸出電流的周期必須相同，即使得這兩種信號同時過零，那么該方法則是通過電流頻率要稍低于或高于PCC點的電壓頻率，從而達到擾動信號注入的目的。圖1是AFD的基本原理圖。圖中Ug是電網電壓，Io是逆變器輸出電流，輸出電流的偏移時間是tz，電網的電壓周期是Tu，輸出電流的周期是Ti。圖1中，電網電壓頻率小于輸出電流擾動頻率，在輸出電流為零時，保持為零狀態，并且持續時間tz，等到電壓頻率為零。在負半周期時，輸出電流的數值與正半周期相反，在輸出電流為零時，與正半周期一樣，同樣保持為零狀態，等待電網電壓歸零。

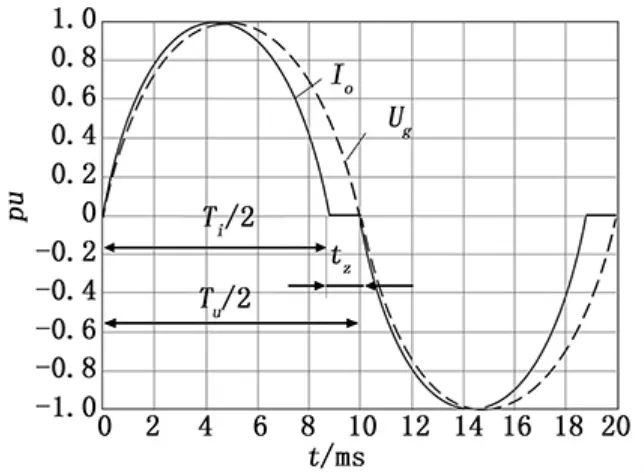
圖1 AFD的基本原理圖

當光伏并網系統正常運行時，注入適量的電流擾動，因為電網的鉗位效果與鎖相環 (Phase Locked Loop，PLL)的存在，使得逆變器輸出電流初始相位能夠正常跟蹤光伏并網系統的電壓相位，這對整個系統的正常工作不會產生影響;但是當發生孤島狀態時，因為電流的偏移和偏移時間tz的存在，使得公共耦合點的電壓Upcc的頻率發生變化，從而形成正反饋，增加了Upcc的頻率偏移量。一旦超過設定的頻率閥值，即可檢測到孤島狀態。

2.2 斬波率與檢測盲區

斬波率 (chopping fraction，cf)是AFD中一個十分重要的參數，它表示系統受到擾動的強度，其大小和電流偏移時間tz和電網的電壓周期Tu有關，即:

在式 (1)中，斬波率cf可以是正也可以是負，當cf為正值的時候，PCC點處的電壓頻率小于逆變器輸出電流的頻率;當cf為負值的時候，PCC點處的電壓頻率大于逆變器輸出電流的頻率。同時，電流偏移時間tz的大小可以隨著cf大小的改變而改變，使得逆變器輸出電流的頻率發生變化。

AFD并網電流函數可表示為:

其中:Im是電流幅值，λ是電流波形的頻率;即在PCC點處電壓相位0≤wt＜π－tz的情況下，逆變器的輸出電流是正半周;在PCC點處電壓相位π－tz≤wt＜π的情況下，逆變器的輸出電流是零;在PCC點處電壓相位π≤wt＜2πtz的情況下，逆變器的輸出電流是負半周;在PCC點處電壓相位2π－tz≤wt≤2π的情況下，逆變器的輸出電流是零。

設電網頻率為f，那么它與電流波形的頻率、斬波率cf之間的關系式是:

此外，斬波率cf不但會對電流波形的總諧波率THD(total harmonics distortion)產生影響，而且也會對檢測盲區產生影響。即檢測盲區是作為判斷孤島檢測方法是否可靠的關鍵參數。若檢測盲區小，則孤島檢測更加可靠，可見減小檢測盲區的重要性。

檢測盲區大小的衡量準則是能夠檢測出的最大負載品質因數Qf，即Qf越大，檢測盲區會越小。其定義為:

式 (4)中:R為負載電路的電阻，L為負載電路的電感，C為負載電路的電容。

由文獻［13］可知，電流的畸變率THD跟隨斬波率cf的增大而增大，同時能夠檢測的最大值Qf也隨之增加，從而使得檢測盲區的減小。所以，在使用AFD法檢測孤島時，通常會在THD與盲區大小之間進行決擇。

3 卡爾曼濾波的諧波估計

在實際工程中，通常會遇到兩類估計問題，狀態估計與參數估計。參數估計是指在已知系統模型中，根據樣本數據來推斷和分析總體的的分布。其方法有同變估計、矩估計和貝葉斯估計等。最基本的方法是最小二乘法和極大似然法。而狀態估計是根據可獲得的量測數據來估算動態系統的內部狀態。最常用的狀態估計法為卡爾曼濾波，主要得益于它響應速度快等特點。由于需要對PCC點進行諧波狀態估計，則對該點的電壓進行建模，其測量方程與狀態方程如下:

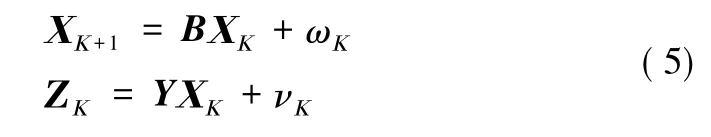
式中，

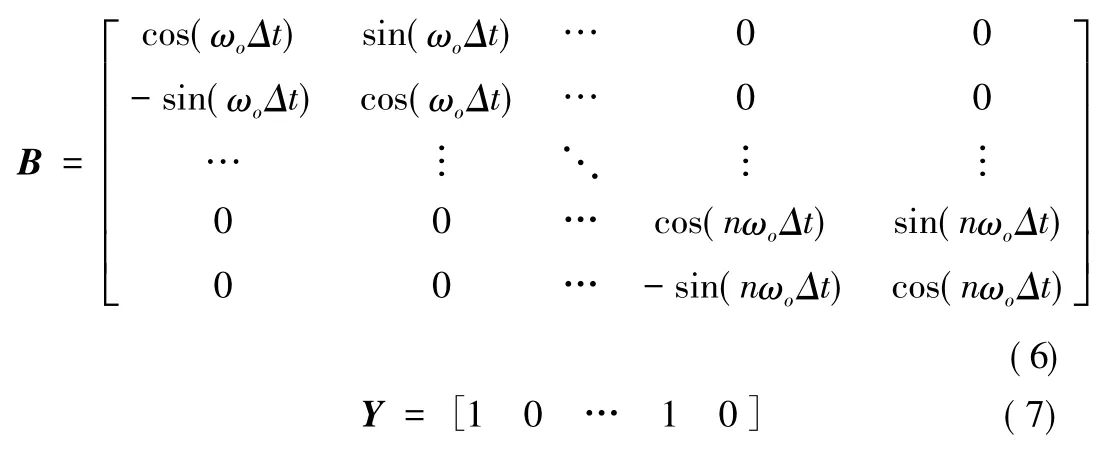
在孤島檢測時，需要得到的諧波狀態估計量為Xk，即PCC點在k時刻的電壓狀態向量;諧波次數是n;電壓在k時刻的測量值是Zk;測量噪聲與狀態噪聲分別是vk與wk，Q是狀態噪聲，R是測量噪聲的協方差矩陣;采樣時間為 Δt。

卡爾曼濾波諧波估計的遞推過程如下:

首先需要初始化，確認初始值Xo、Po、Q和R;其次，每個采樣周期內，進行狀態預測，按下面的迭代方式:

預測誤差協方差矩陣:

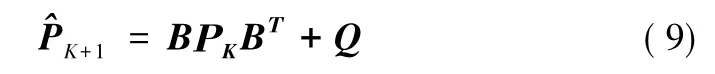
卡爾曼增益:

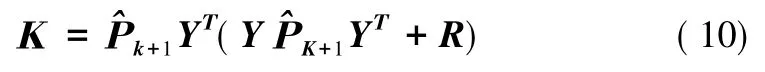
最初狀態更新:

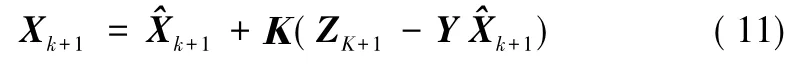
協方差矩陣估計值更新:

然后根據上述步驟中各個時刻的諧波估計值，周期性的計算諧波電壓累計值，公式如下:

其中:n是采樣點數，m是比例系數，用于適當的比例調整，以方便設定孤島檢測閥值。

4 改良的檢測法

當光伏系統發生孤島時，主動頻率偏移 (AFD)法主要是基于負載功率和逆變器輸出功率之間的不平衡程度較大，導致逆變器輸出電流的頻率發生改變，從而檢測出孤島效應。依照IEEE Std 929－2000的規定，電壓頻率的正常波動是在±0.5 Hz范圍，但是出現頻率的波動，表明可能孤島效應已經發生。特別是在某些負載功率和逆變器輸出功率非常接近的情況下，較小的頻率波動無法超出AFD法設定的檢測閥值，使得該方法檢測失敗。如果增大電流頻率偏移量，則斬波率cf也會隨之增大，從而提高了檢測效率，但是輸出電流波形的諧波畸變THD也會增大，這對電能質量會造成較大的影響。如果電流偏移量越小，則會使得檢測盲區的增大，降低了孤島檢測的可靠性。

本文提出了一種改良的主動頻率偏移孤島檢測方法。通過把主動頻率偏移與卡爾曼濾波的諧波估計相結合，組成判斷是否發生孤島的依據。在確保高效的檢測效率與檢測盲區較小的條件下，有效地減少了電流的諧波畸變率THD。

如圖2所示，通過檢測逆變器輸出電流的頻率偏移量F，設定頻率偏移的檢測閥值F1與F2，使F2＜F1，其中在負載功率和逆變器輸出功率不平衡程度較小或者相平衡的情況下，F1的取值要大于其引起的頻率偏移最大量，F2的取值越小，檢測盲區越小;若F1＜F時，采用主要檢測方式，即AFD法來判斷光伏系統是否發生孤島，其中cf的取值如下:

圖2 孤島檢測流程圖

cf0的選取由輸出電流THD來決定，必須保障THD＜5%，頻率偏移量F＜F2時，cf為零。若F2＜F＜F1時，采用協助檢測，即對PCC點的電壓進行諧波估計并計算諧波電壓累計值來判斷光伏系統是否發生孤島。該檢測主要用在負載功率和逆變器輸出功率不平衡程度較小或者相平衡的情況下，通過檢測諧波電壓累加值，來判斷光伏系統是否發生孤島。

5 仿真結果與分析

圖3 光伏并網系統的孤島檢測仿真模型

在Matlab/Simulink平臺上建立光伏并網系統的孤島檢測仿真模型，如圖3所示。一般參數設置要使得負載的功率與光伏發電的功率相等，逆變器輸出的無功功率為0。即電網電壓是220 V，負載的諧波頻率為50 Hz，在功率為2 kW的條件下，負載的取值是R為26.4 Ω，L為88 mH，C為127 uF，其中比例系數m=10，仿真時間設置t=0.4 s。設定在0.2 s時產生孤島效應。當斷開電網時，PCC點的電壓頻率就會產生改變，當頻率大于F2時，即可認為發生孤島效應，此時，通過協助檢測來防止主要檢測方法AFD法失效的可能。同時為了減小THD，式 (14)中cf0所取的值一定要使得THD在5%以內，取cf0為0.02，并且在改變cf的取值時，系統能夠正常運行。設定頻率檢測閥值F2為±0.1 Hz，F1為±0.5 Hz，即 F2＜F1。

圖4所示是負載功率和逆變器功率不平衡程度較大時的仿真結果圖。可見在電網0.2 s斷開時，發生孤島，由于功率不平衡程度較大，使得頻率波動也變大，此時采用的方法是主動頻率偏移檢測方法，斬波率cf0為0.02的情況下，在0.259 s處能夠高效的檢測出孤島。

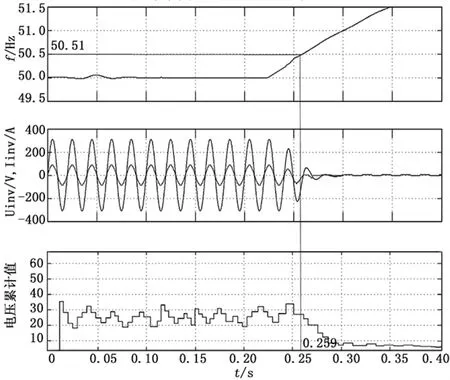
圖4 負載功率和逆變器功率不平衡程度較大時的仿真結果圖

圖5所示是負載功率和逆變器功率不平衡程度較小時的仿真結果圖。其頻率波動范圍較小，沒有超過±0.5 Hz，導致主要檢測方法不能正常啟動，從而采用協助檢測卡爾曼濾波的諧波估計來檢測電壓累計值。本文所設定的閥值范圍是15～45，在電網正常運行時，諧波的電壓累計值保持在小范圍內的波動，當發生孤島時，累計值驟降，低于設置的閥值，從而檢測出孤島。

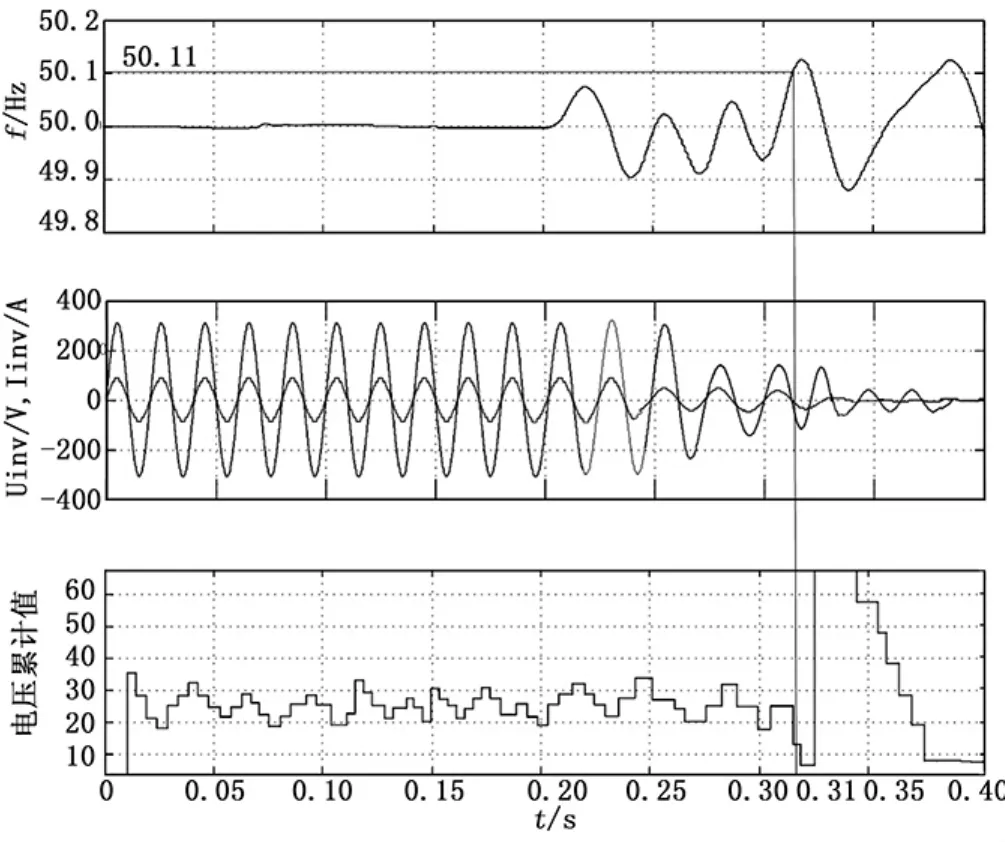
圖5 負載功率和逆變器功率不平衡程度較小時的仿真結果圖

圖6所示是以往的主動頻率偏移法和本文提出改良后的主動頻率偏移法所產生的電流諧波THD比較圖。一般都是在5%以下，但是以往的主動頻率偏移法都會使用較大斬波率cf，用來提高檢測效率，這使得諧波含量較高。但是本文提出改良的主動頻率偏移法通過降低斬波率cf所產生的檢測盲區，由協助檢測來消除，這不但能夠降低電流諧波THD，而且還保證檢測效率較高。另外，以此為基礎，采用不同的斬波率cf進行賦值，使得諧波含量更加減小。

圖6 電流諧波THD比較圖

6 結束語

本文搭建了光伏并網系統的孤島檢測仿真模型，主要針對主動頻率偏移法的不足，提出基于AFD法和卡爾曼濾波的諧波估計相結合的方法來檢測孤島效應，此方法在保障較高的檢測效率條件下，不但有效地減小了檢測盲區，而且降低了輸出電流的諧波含量，提升了光伏系統的可靠性。通過搭建的Matlab/Simulink仿真結果也表明了該方法的優越性。當然，本文也可以進一步優化該方法，例如加入神經網絡算法來提高檢測效率，這是下一步所需要研究的重點。