基于貝葉斯和蒙特卡羅的多信號模型擴展研究

劉欽文

(中國電子科技集團公司第十研究所，成都 610036)

0 引言

測試性是系統或設備能及時準確地確定其狀態 (可工作、不可工作或性能下降)并隔離其內部故障的一種設計特性［1］，在提高執行任務的可靠性與安全性，提高系統可用性，減少系統使用保障費用等方面具有顯著效果，現已大量應用于現代航空航天和武器系統中［2］。

在目前的工程型號項目中，對測試性分析通常采用多信號模型分析法。多信號模型 (multi－signal model)是由Somnath Deb等于1994年提出，屬于相關模型的一種，通過建模分析得到相關矩陣，并可以據此對故障檢測率、隔離率等測試性參數進行預計分析和進行故障診斷。美國QSI公司基于多信號模型開發出測試性工程和維修系統軟件(TEAMS)在航天衛星、航空飛機和汽車等系統的診斷設計、健康管理中得到廣泛應用［3］。

但是傳統多信號模型基于確定性測試假設條件，忽略了十幾種存在的不確定性真實情況，在測試性模型中，相關矩陣只有0、1兩種狀態，故而只能表示故障可檢測或故障不可檢測兩種絕對情況，無法處理故障傳遞和故障檢測不確定性問題，如果忽略這種不確定性，可能產生不合乎實際情況的測試性分析結果［4］。鑒于貝葉斯網絡在處理不確定性問題的優勢，且廣泛應用于故障診斷推理等領域［5-6］，本文也通過引入貝葉斯網絡條件概率的方法，對傳統多信號模型進行擴展，以處理測試不確定性問題。

由于引入條件概率后，故障傳遞和故障檢測存在不能傳遞以及不能檢測的情況，這會引起相關矩陣的變化，由此計算測試性參數尤其故障隔離率會有較大困難［4］，對此筆者提出采用蒙特卡羅法進行仿真模擬，將不確定性問題轉化為單次試驗確定性問題，再使用相關矩陣分析法進行測試性分析。此外利用貝葉斯具有的參數學習能力，通過樣本數據進行參數學習，以消除引入的條件概率可能帶來的主觀誤差。

1 多信號模型

多信號模型是在系統結構和功能分析基礎上，以分層有向圖表示信號流導向和各組成單元 (故障模式)的構成及相互連接關系，并通過定義信號 (功能)以及組成單元(故障模式)、測試與信號之間的關聯性來表征系統組成、功能、故障及測試之間相關性的一種模型表示方法。

主要包括以下元素:

組元c(component):構成系統具有獨立和相對完整功能的可替換的功能模塊。

信號s(signal):系統傳輸特性中能夠清晰描述系統功能的特征屬性。不同信號之間具有獨立性，信號與組元關聯。

測試t(test):在系統某個點檢測某些信號的好壞。

測試點tp(test point):包含測試的測試點。

有向連線l(link):由某個組元指向另一個組元的有向線段，代表著模塊之間的功能依賴關系。

故障與測試之間的相關性是通過定義模塊關聯信號和測試關聯信號的聯系來體現的，并以此為基礎構造故障－測試相關矩陣 (即D矩陣)進行測試性分析。近幾年，基于多信號模型在工程領域的測試性分析得到了廣泛應用［78］，限于篇幅本文不再對多信號模型方法進行詳述。

2 貝葉斯與參數學習

2.1 貝葉斯網絡

貝葉斯網絡 (Bayesian Networks)又稱為信度網絡(Belief Networks)，是目前不確定性知識表達和推理領域最有效的理論模型之一。是圖論與概率論相結合的產物，表示變量間概率依賴關系的有向無環圖。一般由兩部分組成:1)貝葉斯網絡結構，它是一個有向無環圖 (DAG)，由節點和連接節點間的有向邊組成，網絡中的每個節點都表示一個隨機變量，每條邊都表示節點間存在相應的依賴關系。2)節點間的條件概率表 (CPT)，其中的概率值表示了變量間的關聯強度［9］。

貝葉斯網絡為多元隨機變量x={X1，X2，…，Xn}的概率分布提供了一種圖表示，記做＜G，θ＞。其中G=＜N，E＞為有向無環圖，圖中節點Ni∈N，i=1，2，…，n，對應隨機變量Xi，圖中的邊ej∈E，j=1，2，…，m，表示隨機變量間的依賴關系，若Xi依賴于Xj，即圖中Nj到Ni有一條有向邊，則記Xj為Xi的父節點，Xi的父節點集合記為π(Xi)。θ={θ1，θ2，…，θn} 為一組條件概率分布表，其中θi，i=1，2，…，n為隨機變量Xi的條件概率分布表，Xi的取值格局表示為，j=1，2，…J，其父節點集合取值格局記做，k=1，2，…，K，則 θi∈RJ×K可以表示為:

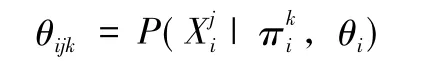
2.2 貝葉斯參數學習

貝葉斯網絡參數學習是指通過對樣本數據的學習，獲得最能匹配樣本數據集的貝葉斯網絡參數，這里的樣本數據即是一組變量的試驗觀測值。在具有完備的數據樣本集情況下，貝葉斯網絡參數學習常用的方法有最大似然估計法和貝葉斯估計法［10］。

二者的主要區別在于最大似然估計法只依據樣本數據與參數的似然程度進行預計，而貝葉斯估計法同時綜合了先驗信息和觀測數據，因此既避免只使用先驗信息帶來的主觀偏見，又避免只使用后驗信息帶來的噪音影響，并且通過將上一次學習的后驗概率作為新一輪先驗概率，在新樣本數據下進行反復迭代學習。鑒于外場收集測試性數據更符合多次小樣本數據的特性，而且可以在各個階段將試驗和使用過程中收集的小樣本數據用于參數學習，逐步迭代修正，因此本文采用貝葉斯估計法進行條件概率參數學習。

此方法分析過程是:

因分析變量參數為［0～1］之間多狀態離散變量，服從多項狄里克萊分布 (Dirichlet分布)，選擇Dirichlet分布作為先驗分布，根據以往對參數θ的先驗知識S，確定先驗分布P(θ|S)，在給定一個完整的實例數據集合D條件下，計算后驗概率P(θ|S，D)。

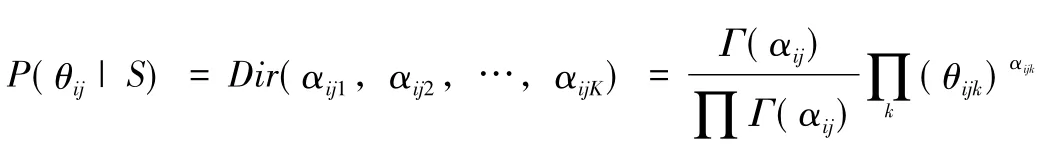
那么，在加入數據集合D后，參數θ的后驗概率也服從Dirichlet分布，可得:

其中:αijk是超參數，且

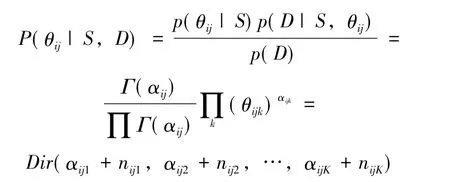
其中:nijk表示數據集合D中滿足條件Xi=xji，π (Xi)=π(Xi)k的實例數，即所求變量在D中出現的次數。此時參數的后驗估計為:

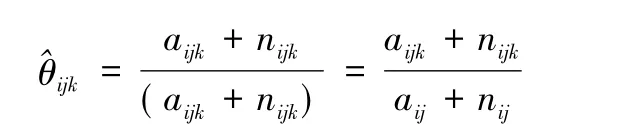
3 實現及驗證

3.1 多信號模型不確定性表示

為考慮系統中故障傳遞和故障檢測的不確定性，引入貝葉斯網絡中的條件概率表 (CPT)概念，用條件概率來表示不確定性問題。通常條件概率表可以分為故障傳遞條件概率表和故障檢測條件概率表兩類，分別如表1和表2所示。

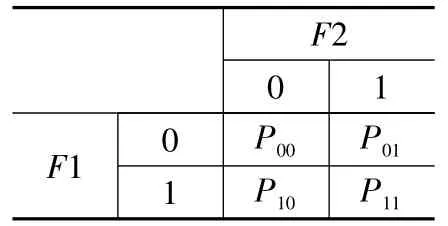
表1 故障傳遞條件概率表

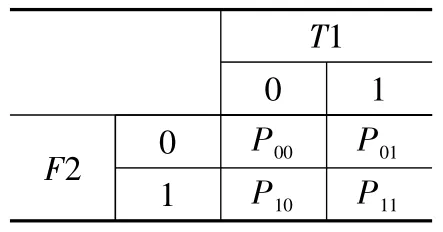
表2 故障檢測條件概率表

以故障檢測條件概率表為例，其中存在4種故障和測試的不確定性狀態，可以用條件概率表示為［11］:

1)P00表示F2不發生時T1檢測顯示正常的概率，即能夠正確檢測到無故障的概率。

2)P01表示F2不發生時T1檢測顯示發現故障的概率，即虛警的概率。

3)P10表示F2發生時T1檢測顯示正常的概率，即故障漏檢的概率。

4)P11表示F2發生時T1檢測顯示發現故障的概率，即能夠正確檢測到故障的概率。

3.2 蒙特卡羅概率抽樣

蒙特卡羅方法 (Monte－Carlo方法)亦稱為概率模擬方法，也稱為隨機抽樣技術或統計試驗方法。它是通過隨機變量的統計試驗、隨機模擬來求解工程技術問題的一種近似解方法。其基本思想是:為了求解一個問題，首先建立一個概率模型或隨機過程，使它的參數等于問題的解，然后通過對模型或過程的觀察或抽樣試驗來計算所求參數的統計特征，最后給出所求問題的解的近似值［12］。

采用蒙特卡羅方法，可以通過對各故障模式進行失效率分布概率抽樣，在一次仿真試驗中得到各個故障模式的失效時間MTTF，其中最小者即認為是這次仿真試驗中故障發生的故障模式 (模擬實際使用過程中的故障發生)［13］。

在單次蒙特卡羅仿真中，對引入的條件概率同樣采用概率抽樣方式處理，將其轉換為確定值 (例如:假設某故障傳遞的條件概率為0.8，單次仿真時，可能存在故障能夠傳遞或不能傳遞兩種情況，但是多次仿真的統計結果滿足傳遞的概率是80%)。在單次仿真中根據得到確定傳遞關系，修正原相關矩陣，相關矩陣的變化會引起檢測次數和隔離次數的變化，從而反映到故障檢測率和故障隔離率上。

通過單次仿真生成的相關矩陣，分析故障發生是否可以檢測，能夠檢測則檢測次數ND+1;再分析是否能隔離到規定模糊度的模糊組，能夠隔離到1個模糊組則NI1+1，能夠隔離到2個模糊組則NI2+1，能夠隔離到3個模糊組則NI3+1。

重復NT次仿真試驗后，得到成功檢測故障次數ND，以及隔離到1個模糊組的次數NI1，2個模糊組的次數NI2，3個模糊組的次數NI3。

由故障檢測率和故障隔離率的定義計算故障檢測率和故障隔離率。

3.3 程序實現

通過MATLAB編輯程序，實現含條件概率表的多信號模型FDR和FIR值計算過程。程序算法如下:

第一步:從EXCEL中導入數據，構造故障傳遞矩陣。此處將其定義為T矩陣，該矩陣直接從多信號流模型生成，反映了故障傳遞的關系以及測試的關系，矩陣中的行對應故障模式，矩陣中的列則包含故障模式、測試點以及失效率和隔離層次信息。假設多信號模型有m個故障模式、n個測試點，則T矩陣的行數為m，列數為m+n+2。

第二步:根據T矩陣，生成D矩陣。首先根據故障模式數量m和測試點數量n，定義一個全為0的m×n矩陣，即D矩陣，然后循環依次查詢T矩陣中各行對應的故障模式列和測試點列的元素，存在傳遞關系 (不為0)，則設置對應D矩陣元素為1。

第三步:進行蒙特卡羅仿真，設置仿真次數為NT。依次查詢T矩陣中含條件概率的元素，并根據概率值進行概率抽樣，單次仿真結果若為0，則需要修改D矩陣，形成新的D矩陣 (定義為D1矩陣)，仿真結果若為1，則直接復制D矩陣為D1矩陣。

第四步:根據D1矩陣，分析是否可檢測以及可檢測后能隔離到的模糊組大小，分別填入D1矩陣中擴展TD列和TI列，形成擴展D1矩陣。

第五步:對各故障根據失效率信息進行概率抽樣，得到各故障模式故障前時間MTTF，比較各MTTF值大小，最小值對應故障模式即認為是該次仿真試驗中發生的故障。查詢擴展D1矩陣中對應的TD是否為1，若為1，表示故障可以檢測，則ND+1，若為0，表示故障不可被檢測，查詢TI數值，若為1，則NI1+1，若為2，則NI2+1，若為3，則NI3+1。

第六步:仿真次數全部完成后，計算FDR和FIR值。

3.4 算例驗證

以圖1所示的多信號模型為例進行說明，模型圖中表示一個外場可更換單元 (LRU)中由兩個內場可更換單元(SRU)組成，SRU1中包含4個故障模式 (F1～F4)和1個測試點 (T3)，SRU2中包含3個故障模式 (F5～F7)和2個測試點 (T1、T2)，其中的連線表示故障的傳遞關系。

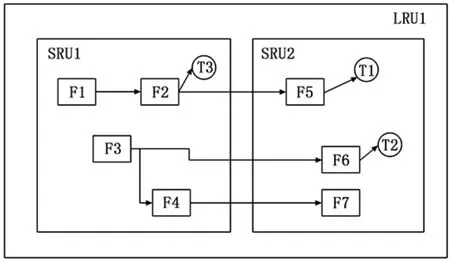
圖1 多信號流模型圖

通過模型圖可以轉化為相關矩陣，見表3，即將某個故障模式對應能夠檢測的測試點用1表示，不能檢測用0表示，由此得到故障－測試的相關矩陣，反映了模型圖中的連接關系。

正如前文所述，基于傳統多信號模型形成的相關矩陣只有0、1兩種狀態，故而只能表示故障可檢測或故障不可檢測兩種絕對情況，無法處理故障傳遞和故障檢測不確定性問題。

現以該多信號模型舉例說明條件概率表在多信號模型中的應用方法，通過專家分析知故障傳遞F1→F2，故障傳遞F2→F5，以及故障檢測F5→T1存在不確定性問題，各自的條件概率表如表4～表6所示。

表3 相關矩陣表格

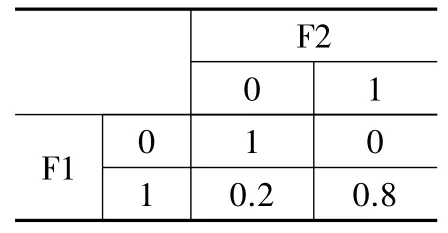
表4 F1→F2條件概率表

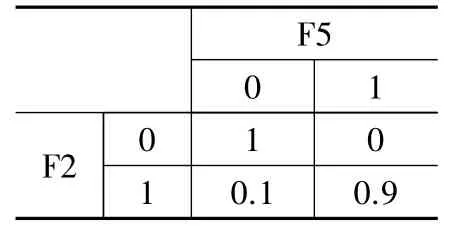
表5 F2→F5條件概率表

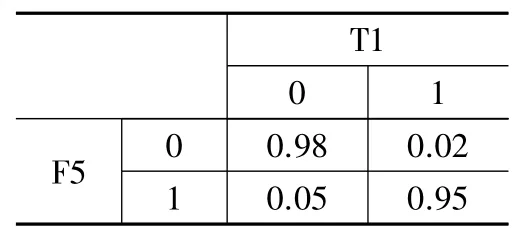
表6 F5→T1條件概率表

各故障失效率如表7所示，故障隔離層次為SRU級。

表7 故障失效率數據

分別對含CPT的多信號模型和不含CPT的多信號模型兩種情況進行程序分析，分析結果對比如表8所示。可知在不含CPT情況下，即傳統多信號模型時，該分析程序得到結果與理論計算結果相符，在含CPT情況下，因增加了測試不確定性，FDR值和FIR值會有變化。

表8 計算結果對比情況

此外，筆者通過多個復雜算例對程序進行了驗證，分析結果表明了程序的有效性。

3.5 參數學習

因在傳統多信號流模型中引入條件概率來表示故障傳遞和故障測試的不確定性，而引入的條件概率值在缺乏統計數據的設計初期只能人為賦予，由此可能會帶來較大誤差，所以隨著設計深入，通過試驗以及使用過程中收集的故障測試反饋數據應能用于迭代修正模型。

如前文所述，將貝葉斯網絡參數學習方法用于該條件概率的學習和修正，鑒于外場收集測試性數據更符合多次小樣本數據的特性，而且可以在各個階段將試驗和使用過程中收集的小樣本數據用于參數學習，逐步迭代修正，而不用花費較長時間收集大量樣本數據后再進行參數學習，因此選用貝葉斯估計法進行參數學習。

還是以5.4節不確定性多信號模型為例進行說明，假設F2→F5故障傳遞概率實際為0.6，并且通過蒙特卡羅生成模擬樣本數據，使用貝葉斯估計法進行條件概率參數學習，分別選取5組每組100個樣本數據和5組每組30個樣本數據進行學習，得到條件概率估計值見圖2，其中橫坐標表示樣本數據采樣次數，初始值為先驗概率，兩條曲線表示不同樣本大小下得到的結果值 (含圓圈線條表示100個試驗數據樣本，含方框線條代表30個試驗數據樣本)。

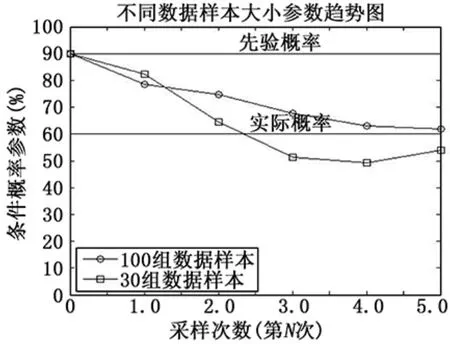
圖2 F2到F5故障傳遞條件概率參數學習結果

從圖可知，進行貝葉斯估計法進行參數學習時，由于同時考慮先驗概率和樣本數據的影響，在沒有樣本數據時，采用先驗概率值，即對應橫坐標為0的數據，隨著不斷的加入樣本進行迭代學習，每次學習后的后驗概率作為下一次學習的先驗概率，因此可以反復迭代，隨著迭代次數增加，結果值逐步收斂到真實值。并且從100樣本數據和30樣本數據對比可知，樣本數據越充分得到的結果收斂性越好。

4 結論

通過引入蒙特卡羅仿真和貝葉斯條件概率，解決了傳統多信號流模型絕對的故障傳遞關系與實際中存在不確定性情況不相符的問題，優化了多信號流模型分析方法，并且通過蒙特卡羅仿真試驗方法，采用原始定義計算測試性參數，避免了工程上使用失效率計算時需滿足指數分布的限制條件，因此可以擴展分析正態分布、威布爾分布等非指數分布的情況。引入貝葉斯參數學習方法利用收集的反饋數據對賦予的條件概率進行修正，消除條件概率人為設置的主觀因素，使結果更加符合實際情況。通過算例驗證了該方法的有效性。

由于蒙特卡羅方法為概率抽樣法，通過多次仿真來模擬產品實際使用過程中的多次故障發生，以此來進行測試性分析，因此該分析流程與實際使用中故障產生、故障檢測、概率統計、分析得到測試性結果的分析方法一致。但由于蒙特卡羅的概率抽樣特性，單次試驗結果具有很大隨機性，需較大的仿真次數規模來保證分析結果的準確性，仿真次數的增大又會導致分析時間增長的問題，尤其在引入條件概率后，計算量大，分析時間長，后續優化程序算法、提高程序效率是還需繼續改進的方向。