基于雙目技術的無人機自主三維定位方法研究

余莎莎，黃 浩，劉泱杰，胡永明，顧豪爽

(湖北大學物理與電子科學學院鐵電壓電材料與器件湖北省重點實驗室，武漢 430062)

0 引言

無人駕駛飛機 (Unmanned Aerial Vehicle，UAV)簡稱無人機，不同于有人駕駛飛機，它是一種無需飛行員控制，可以在遠距離操縱飛行系統的自主飛行器。由于其體積較小、造價較低、機動性較強、隱蔽性較好等突出優點，在21世紀被越來越多地應用在軍事偵查、目標追蹤、地形勘察等領域［1］。

從技術角度的定義可以將無人機進行劃分，但無論是哪種類型的無人機，其完成軍事偵察、目標追蹤、地形勘察的前提都是獲得自身的精確定位［2］。目前高空高速無人機大多采用精密慣導與GPS的組合導航來獲得無人機的實時位置。雖然目前組合導航的精度已經十分地高，但也僅能獲得無人機的二維位置信息。

另外，用于導航的高精密設備造價高、體積大，而用在軍事中的微小型無人機受到成本限制且載荷有限，無法搭載導航所需的高精密設備。且軍用無人機不僅需要工作在無遮擋的室外環境中，也需要工作在有遮擋的復雜場景，如城市和森林等。在這些難以獲得GPS的場景下，無法得到無人機的二維位置信息。為使無人機工作在各種復雜場景中，需要設計不以GPS信息為基礎的短距離、高精度的三維定位方法。

文獻［3］從無人機的需求出發，考慮到小型無人機飛行時的速度、高度和角度等狀態參數，采取將GPS和AHRS以及氣壓測高計相結合的組合導航，通過硬件設計和復雜算法，使得到的控制飛行狀態參數滿足需要，最后通過實際操縱飛行進行驗證。文獻［4］將天文導航技術應用到無人機自定位上，對多星和單星定位算法進行了重點推導;并對這兩種算法進行了細致的分析和比較，并在保持前提條件相同的情況下下進行仿真和分析定位誤差。文獻［5］對微小型無人機在無GPS的環境下的自定位技術進行了研究，通過選擇成本低、質量小的器件，基于智能機器人控制系統構建無人機自定位技術的總體架構，探索出易集成、硬件所需成本低的新型定位技術。基于微機電系統展開對定位架構的研究，參考了當前不同場景下的自定位算法思路，并通過觀察各種算法在無人機的環境適應性，最終探索出一種能適應復雜環境變化及低參數依賴性的自定位框架。

無人機自主三維定位具有很強的自適應能力，可以再不同場景下快速有效地對自身進行定位。它是指在無人為操縱的條件下，自身的系統感知環境和處理信息［6］。基于雙目技術的無人機自主三維定位是指通過固定在無人機上的兩個攝像頭采集圖像，經過圖像處理、圖像匹配和計算得到無人機與預設定點之間的距離，再經過坐標變換計算得到無人機的三維位置坐標的方法。所有的工作均由無人機及其裝載裝備完成，因而具有導航自主性。

基于雙目技術的無人機自主三維定位技術與現有的無人機定位方法比，其定位設備可靠，設備依賴性較小［7］;而且不受時間、地點和環境的限制，其定位誤差既不隨時間的增加而增大，也不會因航行距離的增大而積累。不同于需要收發電磁波的GPS定位，它不需要設立陸基臺站和向空間發射軌道運行體，完全是一種被動式自主測量［8］。此外，不受電磁波的干擾破壞，其可靠性高、隱蔽性好、生命力強，當衛星導航遭受到信號干擾或人為破壞時，啟用基于雙目技術的自主三維定位無疑更具有深遠的意義。

綜上所述，基于雙目技術的無人機自主定位方法不僅可以為在不同場景下飛行的無人機提供更為精準的三維導航信息，它同樣也是被動定位的基礎;同時，在當今軍事戰爭愈發地強調隱蔽性的趨勢下，研究無人機三維自主定位，在用于軍事戰爭的無人機上具有廣泛的應用前景。

1 雙目技術原理

雙目視覺技術是計算機視覺的重要技術之一，由于具有人工智能性，雙目視覺技術被廣泛應用在多種領域，比如:將雙目視覺技術應用在手術機器人上，通過在體外觀測手術器材的運動狀態和姿勢，從而完成對手術器材的精確控制;雙目視覺技術在汽車上的應用，可以檢測到道路信息，反饋給司機實時路況和隨時可能發生的危險;雙目視覺技術還可應用于助盲導航，從而代替導盲犬更加有效地幫助外出行走的盲人［9］。

雙目視覺技術是用計算機對人的雙眼進行模擬，從而感知世界。通過固定的雙目攝像頭同時從不同角度采集兩幅圖片，經過立體匹配技術得到目標物在圖片上的匹配點以及每一點的視差，即該場景中的目標物在雙目攝像頭上投影點的差距，由得到的視差值可以恢復三維場景中目標物的深度信息［10］。

在雙目立體視覺系統中，兩個固定安裝的攝像機作為圖像信號的采集設備，圖像捕捉卡將圖像視頻信號經處理后傳送到計算機或信號處理設備上［11］。最簡單的雙目立體視覺系統，如圖1所示，兩個攝像機沿基線放置，使得Zr//Zl//Xa，Zr為左攝像的光軸，Zl為右攝像頭的光軸。

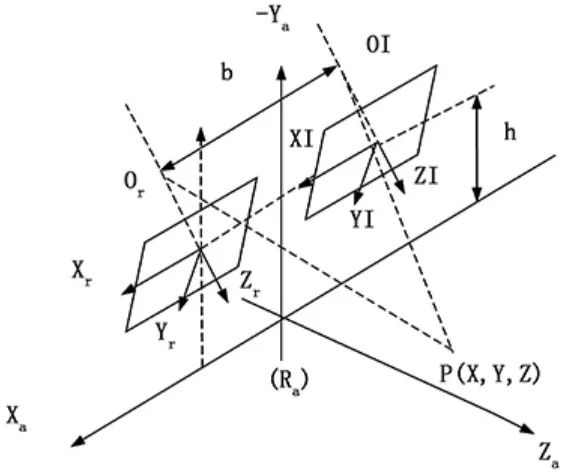
圖1 雙目視覺系統的幾何原理

將物體抽象為質點，如圖2所示，當兩個或多個物體與攝像機鏡頭的光心呈一條直線時，在所得照片上的顯示則為一個點，也就意味著從相片上并不能辨別出這些不同的物體［12］。而雙目視覺利用兩個攝像機從不同位置進行攝像，根據兩者所成的像在兩個相片中對應點的關系來計算物體的深度信息。

圖2 雙目視覺中的匹配點

根據雙目立體視覺的物理圖像和成像原理可以抽取出如圖3所示的幾何關系。

則深度Z的計算公式為:

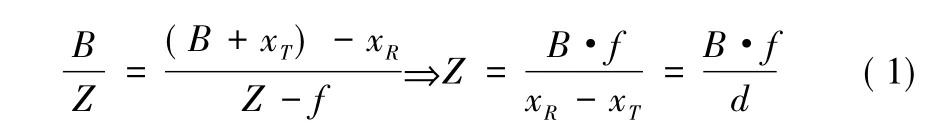
其中:B為基線 (baseline)的長度，表示兩個相機光心的距離;f為相機的焦距;d為視差。

圖3 雙目視覺中的幾何關系

從公式 (1)可以看出，P點距攝像機的垂直距離與雙目攝像機的基線長度B和攝像機的焦距f成正比，與視差d成反比。在成像過程中，雙目攝像機的基線長度B和焦距f保持不變，拍攝出的物體與雙目攝像機的距離與通過算法計算得到的視差成反比。兩幅圖像中計算得到的視差值越小，物體距離攝像機越遠。得到二維圖像的視差圖后，便可以通過公式變換得到該幅圖像每一點的實際距離，從而重建出該相片所拍攝場景的三維幾何模型。

2 基于雙目技術的無人機自主三維定位

2.1 無人機自主三維定位流程

無人機自主三維定位流程如圖4所示，其包含4個主要步驟，總結如下:

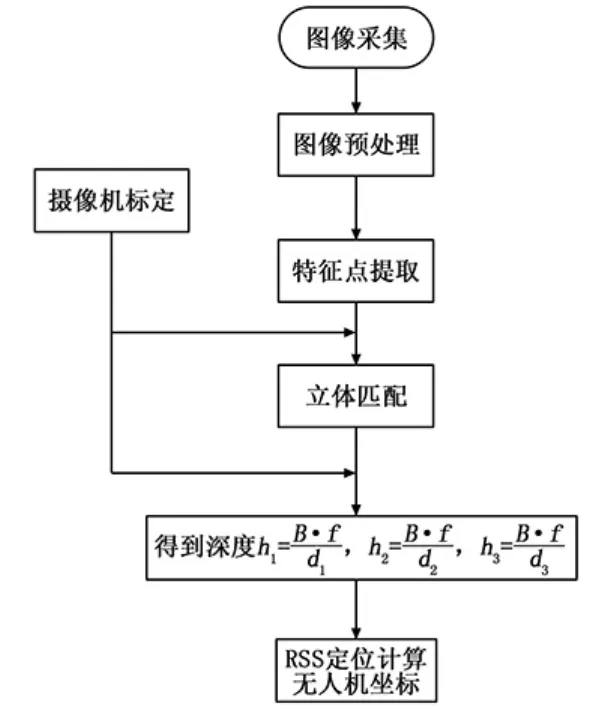
圖4 無人機自主三維定位流程圖

1)將兩個相同的攝像機安裝在無人機底部并規定原點和坐標系，選取地面的3個已知坐標的固定點為參考點;

2)對雙目攝像頭進行標定，同時采集地面的圖像，并對采集到的圖像進行預處理，提取特征點;

3)將采集到的圖像與3個定點進行圖像匹配，得到無人機與3個定點的距離分別為:

4)用RSS定位算法估計無人機的三維幾何位置值。

2.2 無人機的雙目測距實現

無人機自主三維定位方法是將雙目攝像頭安裝在無人機機身上，通過采集并處理圖像，獲得無人機上的待測點與已知坐標的定點之間的深度信息，再通過定位算法計算得到無人機的三維坐標值。

雙目攝像頭固定在無人機的底部，左右攝像頭對稱于機軸，攝像機光學中心的連線平行于水平線，已知基線長度為B。規定水平面為xoy面，與水平面垂直向上的方向為z軸方向，并選擇合適的原點 (該原點是參考原點，對定位精度無影響)。在地面上放置3個不在同一直線上的定點標記，它們形狀不同 (或為3個已知坐標的房屋、建筑等物體)，選取的標準為在無人機活動范圍之內的任何位置都可以被雙目攝像頭捕捉到。已知定點的坐標分別為P1(x1，y1，z1)，P2(x2，y2，z2)，P3(x3，y3，z3)。

圖5 三維定位幾何示意圖

在無人機進行三維自主定位之前，首先對兩個攝像頭進行自標定，得到攝像機的內部參數 (焦距f、成像原點、畸變系數)和雙目鏡頭相對位置關系 (旋轉矩陣和平移常量)。根據攝像頭標定后得到的內部參數和相對位置分別對左右圖像進行消除畸變和行對準，使得兩攝像頭光軸平行、成像平面共面、對極線行對齊。

將兩攝像頭在同一時間捕獲到的圖像與已知的定點標記圖像進行匹配，通過搜索左右像機采集的圖像中的3個定點標記來確定匹配位置。如圖5所示，無人機在空中飛行的時候，在地面上觀測到的無人機為一個足夠小到可以忽略體積大小的點，因此可以將雙目攝像頭抽象為在光心連線中點的質點M。圖中，P1，P2，P3為3個標志物中坐標已知的點，h1，h2，h3分別為點P1，P2，P3到待定位節點M的距離。

2.3 RSS定位算法距離估計

RSS(Received Signal Strength)定位是基于距離的定位，距離估計的精確程度間接反映了定位的精確程度。假設待定位節點M的坐標為 (x，y，z)，由雙目技術測得M點到3個已知定點的距離分別為h1、h2、h3，則有:

此時，M點的坐標 (x，y)可以通過求解下面兩個線性方程獲得。對式 (2)可以重新整理成矩陣形式:

A和B是由實際參數確定的已知向量，X為需要求解的未知向量，可用最小二乘法來求解該矩陣方程。最小二乘算法可具體描述如下:

根據上式定義殘差值e:

殘差的平方:

至此定位問題可轉化為求f(X)最小值的問題。對f(X)求導并令其為零:

可以得到X的解:

所求的X的解即為無人機獲得圖像時的橫縱坐標坐標。

根據已經求得的橫縱坐標 (x，y)可以推算出無人機的高度

至此解算出無人機的位置坐標 (x，y，z)。

3 系統仿真與結果分析

3.1 系統仿真

為檢驗所提方法的有效性與優越性，將通過MATLAB仿真來評估該三維自定位算法的性能。仿真數據均為歸一化的結果。設定無人機在空中以0.95 m/s的速度向與x正半軸成54.43°，與z軸正半軸成29.74°的方向勻速運動。點(0.1，0.2，0.3)為無人機勻速飛行中的一點，并假設該點為0 s時無人機的起始位置。

任意選取3個定點坐標分別為P1(0，0，0)，P2(0.1，0.7，0)，P3(0.3，0.2，0)。雙目攝像頭經過過圖像采集、攝像機標定、圖像預處理，雙目立體匹配等步驟得到無人機 0.1 s，0.2 s，0.3 s，0.4 s，0.5 s，0.6 s，0.7 s，0.8 s，0.9 s，1.0 s時與已知定點的距離。令無人機在第0.1*i秒與Pj點之間的距離為hi，j，其中i=1～10，j=1，2，3，所得的數據如表1所示。

對無人機自主三維定位方法進行系統仿真，輸入表1中的數據，采用上文描述的RSS定位計算方法，計算出無人機每個時刻的三維位置坐標。將每個時刻的三維位置坐標點連接成一條平滑的曲線，由此得到無人機0到10 s內勻速運動的軌跡。無人機的三維運動軌跡如圖6所示。

表1 無人機與已知定點的距離

圖6 無人機在三維空間中的運動軌跡

3.2 結果分析

令Mi為第0.1*i秒無人機的實際位置坐標，已知無人機每一時刻的定位如表2所示。

表2 無人機的實際位置

比較表2中的坐標和圖6中無人機在對應時刻坐標，結果表明:本文提出的無人機自主三維定位方法與實際的三維位置幾乎無差別，該定位方法的精確度較高，定位效果較為理想。

4 總結

基于雙目技術的無人機自主三維定位方法，改善了傳統GPS定位的維度缺失和場景限制等缺點，使無人機的工作場景不再局限于室外無遮擋的環境，而且可應用在室內、森林和城市等弱或無GPS信號的復雜環境。且雙目攝像頭較傳統定位方案，具有成本低、載荷輕、體積小、不受電磁干擾等特點，較適用于高精度勘測偵查用途的微小型無人機。基于雙目技術的無人機自主三維定位方法通過Matlab仿真驗證，結果表明:本自主定位方法實現了無人機的實時精確定位，與無人機的實際位置匹配度高，定位效果較理想。