條子圖之含“雙比”的應用題

劉善娜

【教學時機】

人教版六年級上冊分數(shù)除法單元學習后。“雙比”應用題，是指問題中含有兩個“比”的應用問題。

【教學目標】

1.通過畫包含兩個相關比的應用問題的直條圖，從“份數(shù)”視角進一步理解“比”。比與分數(shù)可以轉化，深度理解比，也有利于形成更簡捷合理的分數(shù)問題解題策略。

2.掌握較為直觀的直條圖的基本畫圖技巧，為后續(xù)分析理解較難的應用問題打下基礎。

【教學過程】

一、理解“比的轉化”

出示題目：甲∶乙=5∶3 ，乙∶丙=4∶3。甲∶乙∶丙=？

師：這兩個比中的誰是不變的？如何統(tǒng)一、轉化？

小結：為了清楚哪個份數(shù)不變，需要統(tǒng)一成一樣的份數(shù)，我們可以把它圈一下。板書：

【設計意圖：兩個相關的比的轉化，是畫比問題的相關條子圖的重要知識基礎。如果學生基礎不扎實，可以多練幾題。】

二、典型問題形成技能：其中一個量不變

2.師生交流，示范作圖。

師：這道題的正確率有些低。如果想掌握更簡單的方法來攻破這類題，就請同學們跟著老師一步一步地畫圖。

【設計意圖：這類單位“1”變化的分數(shù)問題，學生會感到有一定的難度，正確率很低。即便通過分數(shù)問題的方法去找“量率對應”來解決這類問題，學生也覺得非常抽象，不容易理解。因此在學生解答后，教師快速核對答案、統(tǒng)計正確率，激發(fā)學生尋求比“量率對應”更簡單的解題方法的需要。】

問1：畫圖時要先把已知的信息畫出來，這個問題中你能看到兩個比嗎？先畫7∶5，男生∶女生。再畫第二個比，也是男生∶女生，是9∶7。兩個比中，有人數(shù)相同的或者說沒有發(fā)生變化的份數(shù)嗎？

小結：男生人數(shù)沒有變化，所以“9”和第一個比中的“7”一樣長，代表的是一樣多的男生人數(shù)。女生人數(shù)要比原來的長一些，因為多了“12人”。

問2：兩個比中有相同的量，能否把相同的量轉化成相同的份數(shù)？

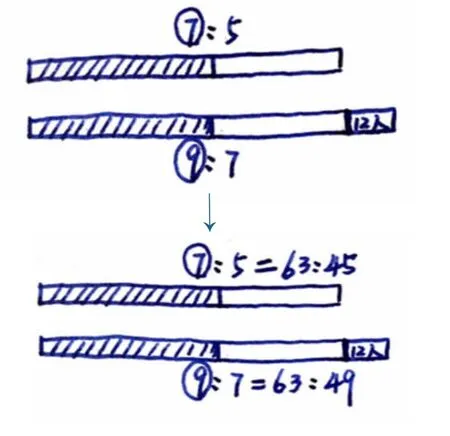
問3：現(xiàn)在，你可以從圖上看到女生“份數(shù)”的變化嗎？

生：女生人數(shù)從45份變成49份，多了4份，多了12人，1份就是3人。男生有這樣的63份，就是63×3=189（人）。

問4：在兩個比的應用題中，畫條子草圖的關鍵是什么？

小結：找到兩個比中相等的或者不變的量，轉化成一樣的份數(shù)，就能從圖中算出1份是多少。

【設計意圖：這類含兩個比的應用問題，屬于比中的其中一個量發(fā)生了變化，總量也發(fā)生了變化，要利用不變的量轉化兩個比，學生就能在條子圖上清楚地看到“份”的變化，從而求出“1份”的量。從直觀出發(fā)，強調(diào)“不變的量”。】

3.嘗試，訓練。

（1）某班女生人數(shù)與男生人數(shù)的比是4∶5，最近又轉來一名女生，結果女生人數(shù)是男生人數(shù)的現(xiàn)在全班有學生多少人？

4.方法小結。

在兩個比的應用問題中，畫條子圖的步驟為：找到不變的量，長度對齊→轉化比，使不變量的份數(shù)相同→觀察變化的份數(shù)。

【設計意圖：第（1）小題完全是模仿性訓練，在交流反饋后進一步歸納作圖方法，強調(diào)畫出“不變的量”；第（2）小題需要轉化一步，通過找出“不變的量”是女生人數(shù)進一步感受找“不變的量”來作圖的基本策略。】

三、典型問題形成技能：兩個量的總量不變

1.呈現(xiàn)問題：修一條公路，已修的與剩下的比是1∶3，再修 30 千米，已修的與剩下的比是 2∶3，這條公路長多少千米？

師：兩個比中，什么量不變？

小結：已修的和剩下的都在變，總數(shù)“一條公路的總長”才是不變的。兩個比的變化問題，可能是其中一個量不變，也可能是總量不變。

【設計意圖：六年級學生要學會分析問題的特征，分析相關問題的異同。因此，呈現(xiàn)略有變化的題型時，要多讓學生說說有什么變化，了解一類問題的類型有哪些，做到心有問題的“全局結構”。】

2.師生交流，逐步成圖。

核心問題：什么量不變？（把不變的圈起來）怎么轉化？

3.模仿跟進。

（2）兩塊一樣重的銅鋅合金，第一塊銅與鋅的比是1∶4，第二塊銅與鋅的比是3∶4，把它們合成一塊，銅與鋅的比是多少？

【設計意圖：第（1）小題是模仿性訓練，與例題一致，仍然強調(diào)畫出“不變的量”，再轉化；第（2）小題不變的總量以“相等”的形式出現(xiàn)，略有變式。畫圖策略上沒有變化，繼續(xù)訓練技能。】

4.再次回顧方法。

四、全課總結

師：關于畫這類條子圖，你有什么收獲？

【教學建議】

兩個比的應用問題，是分數(shù)應用題的一種。教師可以從“份數(shù)”的角度切入，利用畫條形圖所必須思考的“誰與誰對齊，一樣長”的問題，將核心問題從隱性切換到顯性，從“量率對應”的抽象走向“幾份變成幾份”的直觀。在實際教學中，有兩點建議：

一、教學“比”的概念時，強調(diào)“份數(shù)”意義

認識“比”的時候，要讓學生更多地認識其“份數(shù)”的意義。在學生掌握比的概念后，可以將原來較為簡單的分數(shù)問題轉化成比的應用問題，不要將比的應用局限在“按比例分配”問題。

二、后續(xù)再加一個課時，對比溝通“分數(shù)問題”與“比的問題”的畫法、解法

畫數(shù)學課程中有“畫線段圖解決較復雜的分數(shù)問題”一課。當學生學完含兩個比的應用問題后，后續(xù)需要再跟進一課時，關注分數(shù)典型問題和比的應用問題的溝通，對比線段圖和條子圖，發(fā)現(xiàn)其中的聯(lián)系和差異，有助于學生掌握靈動的、聯(lián)通的解題策略，而不是就題論題，就類型畫圖。