例談基于“最近發展區”理論的教學方式改進
心理學認為,人的認知水平可劃分為三個層次:“已知區”“最近發展區”和“未知區”,它們的關系是:已知區→最近發展區→未知區。人的認識水平就是在這三個層次中循環往復、不斷轉化,最終實現螺旋式上升。筆者認為,教學設計不宜停留在“已知區”,而應著眼于學生的“最近發展區”。若問題設計停留在“已知區”(過易),則無法調動學生的積極性,會浪費有限的課堂時間;若問題設計直接至“求知區”(太難),則不能使學生體會到智力角逐的樂趣,會使學生失去信心,使問題失去價值。教學時,如能把握“已知區”與“最近發展區”的結合點來引導學生思考開展教學,不僅有助于學生原有認知結構的鞏固,也有利于將新知識同化,使認知結構更加完善,并最終使學生認知結構中的“最近發展區”上升為“已知區”。
數學知識的學習不是獨立的,而是一個螺旋上升的過程,知識點與知識點之間有著緊密的聯系,有些知識教師不用教,只需加以引導,學生就能進行遷移學習。教師在備課中如能準確把握知識的最近發展區,對教學設計另辟蹊徑,就會對提高課堂教學效率產生立竿見影的效果。
一、把握知識“增長點”,概念教學要簡潔
“真分數與假分數”是一節概念課,一般的教學方法是引導學生學習什么是假分數,并區分它的范圍,可教學后發現學生對假分數的含義難以理解。即使知道分子大于或等于分母的分數叫作假分數,但還是心存疑慮:分子怎么可能比分母大?因為前期學習的分數的意義是這樣表述的:把單位“1”平均分成若干份,表示這樣1份或幾份的數。它強調的是部分與整體的關系,而部分是不可能超過整體的,所以想從分數意義的角度突破這一教學難點,效果不理想。
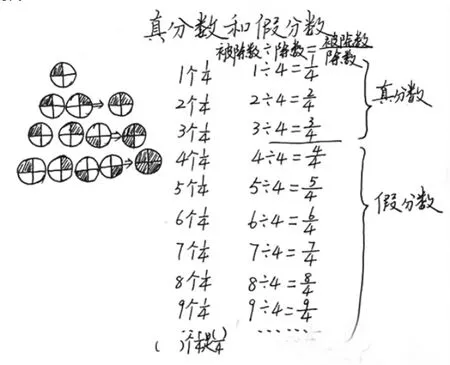
分數知識的“最近發展區”是什么呢?其實利用分數與除法關系: “被除數÷除數=被除數/除數”這一知識作為本次教學的“增長點”,在形式及意義上理解起來反而比較容易。
分數與除法共享平均分的概念,分的過程可以用除法表示,分的結果可以用分數表示,而分的過程又可以理解為分數單位累加的過程。如:通過分圓餅,再建立分數與除法的關系,學生不僅體驗到了分數單位的累加,感知假分數的產生,更是理解了真分數和假分數的含義,體會到了它們之間的區別和聯系。
二、剖析知識的“本質點”,策略教學更到位
“植樹問題”是經典的一節課,有很高的數學思維含量和很強的探究空間。在傳統的教學中,我們一直采用一一對應思想理解“間隔數與棵數”的關系,再幫助學生通過建構數學模型,判斷數學模型,應用數學模型來解決問題。但效果不容樂觀,學生經常混淆到底是+1,還是-1,容易混淆間隔數、棵數、間隔、總長之間的關系。而棵數只跟間隔數有關系,用“間隔數=總長÷間隔”求出間隔數,再判斷模型知道棵樹。但學生對間隔、間隔數這兩個詞理解起來又比較困難,間隔和間隔數是虛擬存在的一個東西,學生也容易混淆。最后,教師只能無奈地指出:植樹問題都要先算出間隔數才行。
其實我們不難發現,植樹問題的本質實際上就是用除法來解決問題,再建構“商+1,商,商-1”的植樹問題模型。而棵樹與間隔數的關系實際上就是“線段圖”,線段圖上的點就是種的樹,點與點之間的“段”也就是所說的間隔,間隔數就是有這樣的幾段(段數)。如果我們將植樹問題的教學轉化到“線段圖”上教學,學生是不是更加清楚呢?
像這樣找準了最近發展區——知識的本質點,難點就顯得不那么難了,其實就是學生之前學過的知識,現在只是加以提升,但本質沒有變。這樣,學生“跳一跳能摘到果子”,學生學得輕松,教師也教得輕松。
三、打通知識“脈絡點”,使圖形教學更深入
圖形教學一般是先讓學生觀察圖形,知道圖形的特征。如長方體和正方體的認識,先讓學生搭一個長方體,觀察發現有6個面,8個頂點,12條棱,再進一步探究兩個面是正方形的長方體。通過這樣的教學,學生學起來比較被動,基本上都能觀察出長方體和正方體的特征,但很難上升到面的特征、棱的特征以及它們之間的關系上,沒有太多的思維含量。這樣一來,學生在接下來計算總棱長、表面積時錯誤率就較高,對于棱的特征、面的特征理解也不夠到位。
圖形起始課教學實際上是為面積和體積計算作鋪墊,起始課學好了,對于接下來的表面積計算和體積計算就是事半功倍了。筆者教學時作了如下調整:
課一開始,揭示課題,再課件出示如下表格:
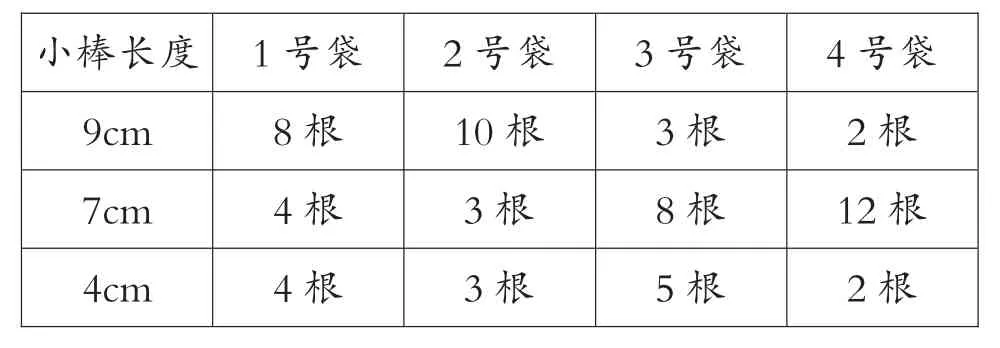
小棒長度 1號袋 2號袋 3號袋 4號袋9cm 8根 10根 3根 2根7cm 4根 3根 8根 12根4cm 4根 3根 5根 2根
這一表格蘊含了本節課中所有要學習的內容,學生在選擇幾號袋時要考慮選幾根,每種長度怎么選,各選幾根。而總共選幾根就是知道了長方體有12條棱長,每種長度怎么選,選幾根有多種情況。比如,選1號袋4根9cm,4根7cm,4根4cm組成一般長方體;選8根9cm就組成兩面是正方形的長方體,這樣的情況3號袋也能做到。選4號袋12根7cm搭成正方體。選好后,再讓學生拿小棒搭成長方體或正方體。在這樣一道思考性極強的題目中,學生不僅掌握了長方體的一般特征,還充分認識了各個棱和面的關系。知道了怎么求棱長總和,知道有兩個面是正方形的長方體中有8條棱相等,其中4個面是一樣的長方形,為后續學習奠定了堅實的基礎。之后,課件出示一個頂點出發的3條棱長(已知長、寬、高),再出示6個面讓學生選擇,進一步加深面的認識。
四、抓住學生的“話語點”,思路點撥要及時
教師的教學要以促進學生的學習為目的,這就要求不僅要在教學上改變,對學生的生活經驗和知識經驗也要深入研究。在平時的教學中,教師應多多關注學生的生活經驗和思維水平,從而準確把握學生的最近發展區。
比如,三下學習連乘和連除的問題時,有這樣一道問題:52型拖拉機,一天耕地150畝,12天耕地多少畝?
一位學生是這樣解題的:52×150×12=……
接下來就出現了這樣的師生對話:
師:告訴我,為什么這么列式?
生:老師,我錯了。
師:好的,告訴我,你認為正確的該怎么列式?
生:除。
師:怎么除?
生:大的除以小的。
師:為什么是除呢?
生:老師,我又錯了。
師:你說,對的該是怎樣呢?
生:應該把它們加起來。
顯然,這位學生是在瞎猜,因此,為了幫助學生找到正確的解答,教師又開始啟發。
師:我們換一個題目,比如你每天吃半個大餅,5天吃幾個大餅?
生:兩個半。
師:怎么算出來的?
生:兩天一個,5天兩個半。
從這位學生的話語中,我們可以了解到學生對于這類問題并沒有真正理解,但只要通過借助熟悉的生活情境來啟發他,解題過程就簡化了。由此可見,有些數學問題與學生生活實際偏離太大,后進生無法快速地將其聯系起來。教學時,教師恰當地利用學生的生活經驗來啟發教學,學生理解起來就會更加容易,也更感興趣。
五、搭建文本“橋梁點”,難點突破要形象
學生在學了兩位數乘兩位數這一課后碰到這樣一道題目:電影院共有21排座位,每排可坐26人。我們想組織500名學生看電影,坐得下嗎?
有位學生這樣問:老師,我有個問題,我想了很久沒想明白。剛才計算26×21,我是用25×20=500來估算的,這樣的話兩個乘數都少了“1”,就是少了一個26和一個21,那么500加一個26和一個21,應該是547,怎么就比大家的答案多“1”了呢?
其實這位學生想的我們用圖形一表示就清楚了:他用長方形表示一個電影院的座位圖,一排26個座位,有21排,先算25×20,再算26+21,在右下角有一個交叉的位子,問題就在此,26+21時重疊了一個座位,所以就比正確的答案多“1”了。
教學時,我們也會碰到類似的問題,如果教師知道知識的背景,及時尋本挖源,就可以幫助學生理解,從而有利于提升學生數學的學習能力和數學問題的解決能力,更有助于培養學生的發散性思維。
六、啟發學生的“懸念點”,預習輔導要有效
比如,很多教師上公開課時,都喜歡選擇“平行四邊形的面積”這節課,但筆者幾次聽這節課都發現同一個問題:教師都是遵循常規教學流程,在教學的引入環節,設疑:你能求出這個平行四邊形的面積嗎?而學生也都能熟練地說出平行四邊形的面積公式,并用公式計算圖形的面積。但對此,很多教師都是采取冷處理,硬把學生拉回到數方格中,再組織學生通過割補把平行四邊形轉化成長方形。練習時有學生又會出現用底邊×鄰邊求面積的情況,學生雖然知道了平行四邊形的面積計算公式,卻沒有真正理解公式是怎么探究出來的。
因此,筆者認為,在教學時,教師可先讓學生預習相關內容,在診斷學生預習情況的基礎上,刪繁就簡,合理用力,實施與學生需求相匹配的針對性教學。平行四邊形的面積公式學生會了,教師就大方地寫在黑板上,然后問學生為什么是底×高?再引導學生將前面學習的正方形面積公式推導遷移到本節課中,滲透轉化思想,這樣預學后教,以學定教,就可以大大提高教學效率。
以上這些現象在小學數學教學中并不少見,如果教學不深入,浮于表面,學生就很難對所學內容充分理解,多數只能做到“知其然”,獲得的僅僅是“事實性知識”,是機械、淺層次的,而數學學習引向深入,讓學生求甚解、會質疑、能驗證。教育家余文森的“三講三不講”原則:已經會的不講;自己能學會的不講;講了也不會的不講。講易混、易錯、易漏點;講想不到、想不深、想不透的;講解決不了的。教學應該是學生現有起點上的生成與發展,能否正確設定學習起點決定了一節課的教學是否具有適切性與有效性。如果教師能夠準確把握學生的起點,找準“最近發展區”促進學生思維的積極投入,高水平地理解和掌握學習內容,實現可能達到、應該達到的發展水平向現實發展水平的持續轉化,課堂教學就一定會精彩無限,更加有效。

