《平面向量》解題錯因探析及預警教學策略研究
周巧菊 寧文輝
(湖南省常德市鼎城區第一中學 415101)
一、問題的提出
《平面向量》作為高中數學的一塊重要內容,它在數學領域應用很廣,這決定了它的基礎地位.在數學教學中,國內國外有很多教師對向量的教學已有較深的研究.學生在學習平面向量時,常出現的一些典型錯題,筆者也有一些研究.
二、平面向量中的典型錯題
平面向量是數學中基本和重要概念之一,是溝通代數和幾何的重要工具,在實際中也有廣泛的應用.通過學生的典型錯題,錯因探析,形成預警教學策略,這樣能讓學生正確理解和掌握平向量有關概念,形成嚴謹的數學思維,提高學生的邏輯分析能力和解決問題能力.
1.平面向量的有關概念
例1 (教材P78第6題(1)、(4)問)判斷下列結論是否正確:
(1)若a,b都是單位向量,則a=b.
(2)直角坐標平面上的x軸、y軸都是向量.
易錯解答:(1)對;(2)對.
正確解答:(1)錯;(2)錯.
錯因探析向量的概念有兩個基本要素:向量的大小(模)與方向.向量的有關概念的理解應抓住這兩個基本要素.相等向量是長度相等且方向相同的向量,而單位向量是模等于1個單位的向量,兩個單位向量的方向并不一定相同;而x軸、y軸只有方向,沒有大小,因而不是向量.這兩個小題的錯因都是概念理解不到位,屬于思維中的大前提錯誤.
預警教學策略此類概念錯誤在學生初學時極易出現,在教學時教師注重引導學生對基本概念的理解,形成清晰的判斷標準.具體地,可把一些易混淆的概念放在一起讓學生自己進行比較辨析,加深學生對基本概念的理解.
例2 下列向量中,可以作為基底的是
A.e1=(0,0),e2=(-1,2)
C.e1=(3,5),e2=(-6,-10)
D.e1=(1,-2),e2=(5,7)
易錯解答:選A. 或選B、C.
正確解答:選D.
錯因探析平面內兩個不共線的向量叫做平面內所有向量的一組基底.對這個命題,學生在學習時只是機械地接受,并沒有獲得本質上的理解.反之,如果兩個向量共線,那無論怎么線性組合都只能表示出與之平行的向量,而不能表示與之不平行的向量.零向量是一個特殊的向量,大小為0,方向可以是任何方向(向量不能沒有方向).選A的學生忽視了零向量與任一向量共線的性質,A中的兩向量e1,e2是共線向量,不是一組基底;選B或C的學生是對基底的概念并不理解.此題的錯誤屬思維中的大前提錯誤.
預警教學策略為了避免學生出現此類錯誤,教師在講授平面向量的基底這一概念時,要強調兩個向量不共線,自然一定是非零向量,可以通過問題的反面設計,讓學生理解作為基底的兩個向量為什么不能共線;為什么零向量與任何向量共線.
2.平面向量的夾角問題
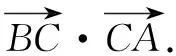
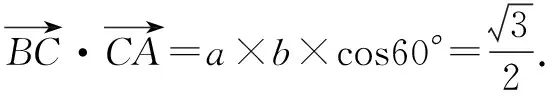
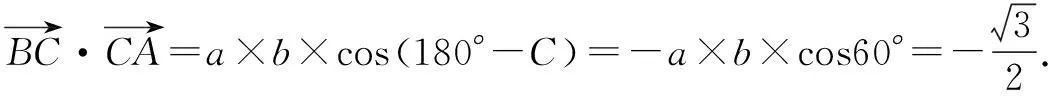
錯因探析這類錯誤發生的頻率比較高:有的學生是沒有理解兩個向量夾角的概念中必需是有相同的起點( 這個小題的錯因都是概念理解不到位),因而屬于思維中的大前提錯誤.
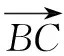
3.共線向量的特殊性
例4 (教材P120第1題(7)問) 若平面向量a,b,c兩兩所成的角相等,且∣a∣=1, ∣b∣=1, ∣c∣=3, 則∣a+b+c∣等于( )
易錯解答:錯選A. 認為向量a,b,c兩兩所成的角相等,它們兩兩的夾角為120°,
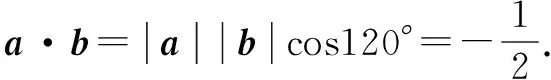
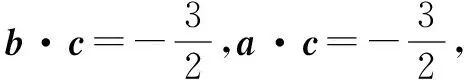
正確解答:因為向量a,b,c兩兩所成的角相等,
(1)當向量a,b,c共線時,它們兩兩的夾角為0°,所以,a+b+c=a+b+c=1+1+3=5.
(2)當向量a,b,c不共線時,它們兩兩的夾角為120°,以下同錯解.故應選C.
錯因探析在利用題中的條件平面向量a,b,c兩兩所成的角相等時,學生忽視了向量a,b,c共線同向的情形,考慮問題不嚴謹,屬思維中的小前提錯誤.
預警教學策略由于學生的思維缺乏嚴謹性,在考慮問題時常常會對一些顯而易見的東西不加注意,三個向量兩兩所成的角相等,學生確實很容易忽視三個向量共線同向的情形.在數學教學中如何培養學生思維的嚴謹性的確是數學教師應該引起重視的,就這個錯解而言,指導學生發現并糾正錯誤不難,要有效地預警教學則是很不容易的.要培養學生具有質疑的思維品質:三個向量所成的角兩兩等,除了成120°的角,還有其他可能嗎?即使這樣,還是有可能想不到0°,還需要思維的敏銳性.應該說這是一個長期的潛移默化的教學過程.(所以在兩個向量的加法和減法的幾何意義教學時就需強調,加深理解向量共線的情形)
三、結語
“學生的錯誤都是有價值的(布魯若)”.我們老師在課堂上要轉變觀念,讓學生暴露錯誤,解讀學生錯誤,了解學生錯誤背后的障礙,錯因探析,形成預警教學策略.讓錯題幫助學生理解和掌握平面向量的基本知識,讓錯題體現價值.在這一個過程中,巧思妙用,讓錯題展示魅力,提高了學生分析問題、解決問題的能力,學生數學素養得到提升.

