試論初中生數學解題方法

呂艷茗 林英姿

臺州市黃巖區北城中學八（2）班 浙江臺州 318020

初中數學難度的上升，使得學生的學習壓力更大。面對不斷增加難度的數學題目，若是仍以傳統題海戰術進行學習難以有效提高自身的解題能力。因此，我們在學習數學知識時，應注重解題方法的運用，確保自身能將規律性的方法掌握。鑒于此，本文主要對初中數學解題中常用的幾種方法進行了分析，幫助學生明確解題思路，以便將解題規律掌握，最終實現提高學習效率、環節學習壓力的目的。

一、配方法

配方法指的是利用恒等變形的方法將一個解析式中的部分項配成一個或多個多項式正整數次冪的和形式，是學習過程中一個重要的恒等變形方法。針對數學問題采用配方進行解決的方法便是我們常說的配方法。而配成完全平方式是我們使用的最多的一個方法。該方法有著十分廣泛的應用，如解方程、化簡根式、因式分解、證明等式與不等式、解析式及求函數極值等多方面內容中都可應用該方法。

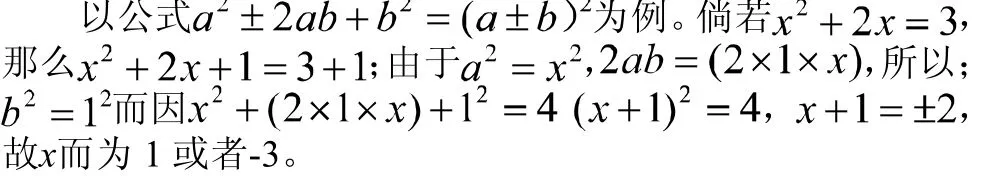
二、因式分解法

該方法是恒等變形的基礎，主要是指將一個多項式朝著幾個整式乘積進行轉化的形式。在數學學習中，該方法是一個有力的工具及數學方法，被廣泛應用于代數、幾何及三角等多個內容的解題[1]。由于因式分解方式較多，不但包含課本教材中提及到的十字相乘法、分組分解法、提取公因式法和公式法等，還包含待定系數法、換元法、求根分解法和拆項添項法等。

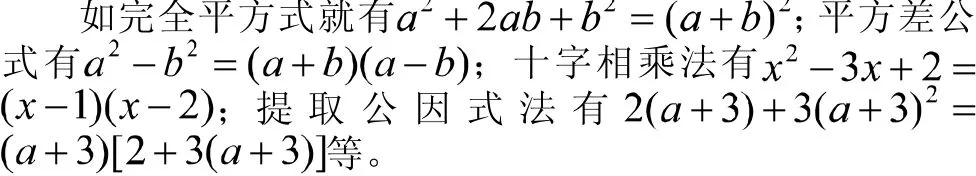
三、換元法

在數學解題方法中，換元法極其重要，具有十分廣泛的應用范圍。通常情況下，我們會將未知數或變數當作元，而換元法指的就是用新的變元將一個較為復雜的數學式子中的部分取代或是對原有式子進行改造，將其簡化，以便將問題解決；也可以理解成數學題解答過程中，通過一個變量取代某個式子，以此簡化問題的方法便是換元法。整體換元又可以叫作局部換元，表示的是已知或未知中重復幾次出現了某個代數，采用一個字母將其取代進而實現問題簡化。

四、判別式法與韋達定理

五、反證解題法

相對于正面解題思路而言，反證解題法的主要區別在于該方法預先提出完全不同于命題結果的假設，隨后再以該假設為根據當作起點，在邏輯層層推理之下，將兩者之間的矛盾推導出來，進而斷定該假設屬于假命題，從反面將原命題判定為真命題。反證解題法主要包含歸謬反證法和窮舉反證法兩個內容。反證法命題證明過程通常由提出假設、進行歸謬、求出結論等三個內容組成。

該方法首先需要提出反面假設，在假設提出之前，需將部分反設術語具體像掌握，如是否平行、是否存在、是否垂直、大于或小于、等于或不等于，至少有個與至多有個等。而對于反證解題法而言，歸謬是其最為關鍵的一點，盡管矛盾推出過程充滿了靈活多變性，然而反面假設認識最基礎、最重要的依據，否則就無法順利開展推導。導出的矛盾通常情況下包含的類型有自相矛盾、與反設矛盾，或是與已知公式、定理、定義及公理矛盾等。

六、結語

數學學科屬于其他理工科課程學習的重要前提及基礎，能在很大程度上影響到我們的日后工作與生活。倘若我們能夠掌握靈活、有效的數學解題方法，所發揮的作用是事半功倍的。具體來說，我們在數學知識學習過程中，必須要分辨課程內容的重難點，通過不同途徑探索與自身相符合的解題方法，以此推動自身數學思維及解題能力的提升，最終提高數學成績。