課堂巧設計 “練”出思維力

江蘇省如皋經濟開發區第三實驗小學 王蓓蓓

2017年11月8～10日，筆者有幸參加了第十三屆小學數學教學改革觀摩交流展示培訓活動，各省的金牌好課匯集于此，聽后讓我收獲滿滿。這些課盡管課型不同，老師教學風格不同，但都有一個明顯的共同點，那就是特別注重在探究學習中提升學生思維力。思維力是個比較大的概念，它包括理解力、分析力、綜合力、比較力、概括力、抽象力、推理力、論證力、判斷力等能力。它是整個智慧的核心，參與、支配著一切智力活動。一個人聰明不聰明，有沒有智慧，主要就看他的思維能力強不強。要使自己聰明起來、智慧起來，最根本的辦法就是培養思維能力。

根據我的理解，我梳理了大師們的幾點做法：

一、創設情境，激發思維

創設情境是指教師在教學中利用模型、實物、錄像等輔助性手段,又或者是利用學生生活中、人的生產實踐中的某些事物,為學生營造與學習有關的情境。

例如，在講“毫升和升”這一知識的時候,老師創設了一個上游泳課的情境：游泳課結束后，如果每個學生要滴4滴眼藥水，50人一個班，需要帶幾瓶眼藥水？

這個情境的設計很貼近學生生活，沒有生搬硬套的痕跡。學生在教師的引導下明確，要解決這個問題得知道一瓶眼藥水，也就是10毫升可以滴多少滴？在交流中又發現：10毫升太多了，可以只研究1毫升有多少滴。于是接下來學生經歷從猜想到實驗，再到計算問題的解決的有效研究過程。

二、激發動機，激活思維

動機是為實現一定目的而行動的原因。心理學研究表明，人的大腦思考是受動機刺激的，沒有動機的思考只能是本能的重復和再現。

例如，“生活中的比”這節課，在引入新課環節，老師是這樣來誘發學生的思維動機的：老師出示了孩子們非常熟悉的班上一個同學的照片，然后動畫演示變化過程，提問：“（1）這些照片和原來的照片比，哪些像，哪些不像？（2）照片的像與不像與什么有關？”像與不像是學生能根據生活經驗直接判斷的，但至于為什么像？為什么不像？像與不像又和照片的什么有關系呢？這兩個問題一提出，學生的好奇心一下子被激發出來了，興趣非常濃，并由此產生了思考。學生開始關注照片的高度、寬度、面積……從多種角度去考慮，想到了像與不像應該和照片的長和寬有關，老師再引導：那可能與長和寬的什么有關系呢？學生猜想長和寬的積、長和寬的商……接下來就是用數據說話，讓學生開展研究。

當然，學生興趣的激發、學習動機的激發，還要體現在新課引入與課堂小結之外的其他環節上，即體現在其他的教學過程中，此過程中的每一個教學環節，教師都需要想辦法讓學生的思維被激活，并且跟學生的學習實際與教師所要教學的內容結合起來，然后通過一些問題去讓學生的思維更加活躍，這樣可以讓課堂學習更加活躍。

三、逐步遞進，發展思維

研究表明，學生在學習中的思維具有明顯的連貫性，即在學習的過程中，在探究未知的過程中，思維必然具有連貫性。所以，教師在教學中需要努力讓學生進行聯想，以讓思維具有層層深入的特點。如果在學習過程中學生的思維能夠逐步深入，那教學效果就可以得到保證。而思維深入可以從橫向與縱向兩個角度來進行。

縱向思維就是指從問題解決的邏輯出發，不斷思考問題解決的思路，以讓學生探求問題解決的源頭。有效的策略就是教師通過問題的連續提出，讓學生一個接著一個思考，一個問題連著一個問題，這樣學生的思維就有了階梯，學生也可以在知識的內在聯系上獲得知識的掌握與思維的培養。

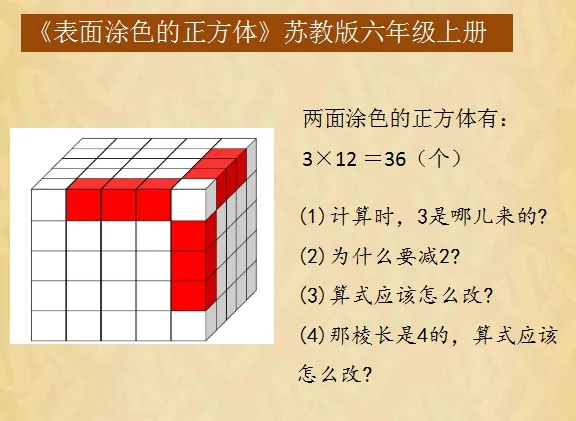
例如,在講“表面涂色的正方體”時,學生研究棱長是5的正方體后，老師向學生提出這樣一些問題：（1）計算時，3是哪兒來的？（2）為什么要減2？（3）算式應該怎么改?（4）棱長是4的正方體，算式可以怎樣改？通過讓學生思考這些問題，層層深入，初步建立模型意識。

所謂縱向思維，其實就是學生在學習的過程中用大腦加工形象的知識，然后向抽象的知識過渡，這樣形象思維與抽象思維相結合，學生的思維能力就可以得到充分的培養。教學經驗表明，學生在數學學習中的橫向思維，能夠促進學生由此及彼地思考，這是一種重要的思維方式，其可以讓學生的知識面更加寬廣，可以讓學生的思維更加具有寬度，在教學中我們常常強調讓學生舉一反三，實際上就是橫向思維的結果。

四、綜合分析,升華思維

分析綜合是思維的基本形式，有了分析，思維才能深入，認識也才能深入，才能提高。分析與綜合之間是相互依存、相互促進的關系，在教學中常常采用先分析再綜合并以此循環的模式，這樣有助于培養學生的創造力。

例如, “用數對確定位置”一課,引導學生觀察數對與圖形的關系，分析：（1）如果行都加相同的數，列不變，圖形會怎樣？（2）如果列都加相同的數，行不變，圖形會怎樣？（3）如果行和列都加上一個相同的數呢？（位置變化，大小和形狀不變）（4）如果行和列都乘一個相同的數，圖形會怎樣呢？（位置變化、大小變化，但形狀不變）這樣一層一層地進行分析,讓學生把握知識的脈絡和思路,最后再進行總結,從而使學生明確數對和圖形之間的邏輯關系。

數學是思維的體操，數學課堂就給培養思維力提供了時間和空間，而作為課堂的主導者，教師就應該用智慧和經驗引領課堂，讓學生的思維力在學習中得到有效的提升。