好題多解 益處多多

吳婧怡

(河北省樂亭第一中學 063600)

一道好題往往可以從多角度、多方位進行思考，雖然解題的思路、方法有所不同，但獲得的答案是相一致的，多解問題可以激發我們的學習靈感，有利于我們的思維開闊.另外，對同一問題采用多種方法進行分析研究，也有利于我們充分認識問題本質，加深對所學知識的理解.

一、考題呈現，引出下文

在△ABC中，AB=AC，AC邊上的中線長度為9，當△ABC的面積最大時，AB的長度為( ).

本題主要考查三角形基礎知識，需要我們充分利用三角形的相關定理、公式來解決，同時幾何問題對我們的識圖能力也要求較高，需要我們從中提煉基本圖形，運用基礎知識來解決.本題屬于中等難度的試題，可以通過多種方法解決，我們要充分利用該類多解題，尤其是在備考階段，合理利用可以起到事半功倍的學習效果.

二、不同角度，解決問題

1.巧用中線，計算面積

評注上述解題過程主要利用的是三角形的中線長公式，得到了x與y的關系，再利用等腰三角形的中線，即垂線的性質，進一步得到三角形的面積表達式，最后結合基本不等式，得到了另一個x與y的等量關系.

2.突出重心，利用性質

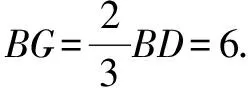
評注上述解題過程，聯想到了BD與AE的交點G恰好為△ABC的重心，所以可以利用三角形的重心性質，因此我們可以在直角三角形GEB中設出關于邊長的未知數x和y，再利用基本不等式求出三角形面積取得最大值時的AB長.

3.直角坐標，事半功倍

評注我們在求解平面幾何問題時，采用構建平面直角坐標系的方法可以將幾何條件坐標化、參數化，并通過各點的坐標值建立起相應的等量關系，有利于后續的數形結合分析，因此該種方法可以極大的簡化解題步驟.

三、總結提高

好題多解，即從不同的角度來分析同一問題，并利用我們所學的知識，充分挖掘已知條件與結論之間的關系，然后利用不同的方法求解問題答案，多解的學習過程，可以有效鍛煉我們的解題思維.另外對不同的解法進行分析比較，可以使我們深刻認識問題的本質所在，而探尋問題的最優解法，潛移默化中就可以提高我們的解題能力.