“一招擊中”高中數學
——芻議數學語言在高中數學中的應用

吳曉慧

(江蘇省如東縣馬塘中學 226401)

高中數學語言分為三種類型：符號語言、文字語言以及圖形語言，這三種語言之間可以通過一定形式進行轉化.學生只有掌握了良好的數學語言轉化能力，才能充分理解數學問題，從而找出解決數學問題的方法.

一、數學語言能力在高中數學解題中的重要性分析

1.數學語言能力是解決數學問題的基礎和關鍵

數學語言能力也可以成為數學語義理解能力，是指學生對數學問題中的公理表達意義、條件、定理、結論、概念以及公理表達關系等的解讀和理解能力，從定義上講，這種數學語義理解能力包含三個層面，首先是數學語言信息、其次是信息之間的相互關系、最后是數學語言名詞的理解能力.數學語言理解能力中包含了對數學題目中隱含條件的查找能力以及辨析數學定義的能力.在高中數學學科教學中，學生的數學語言能力越高，其解決數學問題的能力越強.比如給出數學式子：“a2+b2”，學生不僅要知道這一式子代表了兩個數的平方和，還要有根據此式子聯想出勾股定理、距離公式以及均值不等式等概念.這樣學生才有能力解決基于這一式子的其它數學問題.

2.數學語言能力能夠拓展學生的解題思路

數學語言能力包含了同種語言和多種語言之間的轉換能力，這種能力是學生對數學語言不同表達形式的轉換能力和同種表達形式的內部等價轉換能力，這種能力是學生解決數學問題的先決條件，能有效地幫助學生解決表達形式復雜的各種數學問題.提升了學生的數學理解能力，也拓展了學生的解題思路.掌握良好的數學語言能力能提高學生的數學成績，所以在高中數學教學中，教師應采取有效的措施提高學生的數學語言轉換能力.

二、數學語言轉換在高中數學教學中的實踐應用研究

1.同種語言的轉化

首先是文字語言與文字關鍵詞之間的轉化，以某一題型為例：某人的月收入與其完成的任務量呈一次函數關系，如果他這個月完成的任務量在50單內，則他每單獲得的收益是70元，如果他完成的任務量超過了50單，則每單的收入是90元.如果小明這個月完成了60單任務，那么小明這個月的工資是多少元？這段文字可以提取出的信息有：“任務量、每單收入、一次函數”等.因此，將文字中表現出的關系用y和x表示y=ax，小明完成60單，每單價格90元，這兩個條件屬于文字語言，其中“60、90”是文字語言中的關鍵詞，將文字語言轉化成文字關鍵詞，再將文字關鍵詞代入一次函數關系式中，就完成了對這道數學問題的解答.即a=60，x=90，小明的收入y=60×90=5400元.

其次是符號語言與符號語言之間的轉化.這種轉化關系常見于集合問題中：集合B滿足公式x2-2x-3=0,這一公式屬于符號語言，將這些符號語言化簡就可以解決問題，得出B集合是{-1，3}.

2.兩種語言之間的轉化

首先是文字語言轉化為符號語言，例如在某一數學問題中，已知f(x)是二次函數，則根據題意，可以將f(x)表示成f(x)=ax2+bx+c.這樣就完成了文字語言與符號語言之間的轉化.兩種語言之間的轉化可以幫助學生將圖形、文字等信息變成容易得出答案的符號或數字信息，文字語言轉化為符號語言是解決某些數學問題的基礎和前提，在解決數學問題的過程中具有不可忽視的作用.

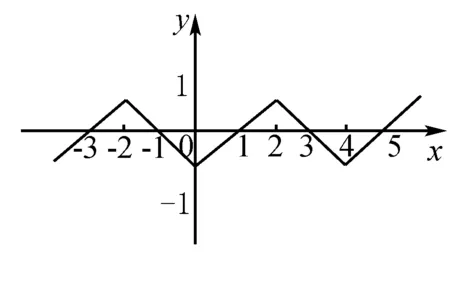
其次是文字語言和圖形語言之間的轉化.比如某一數學問題中已知f(x)是偶函數，它的周期為4，當x在0至2的區間時，f(x)可以表示為x-1.根據題意可以將題目中的文字信息表示成如圖所示.

這種圖形語言相較于文字語言來說更加直白，有助于學生理解，提高學生答案的準確性，是高中數學教學中解決問題的有效方法之一.

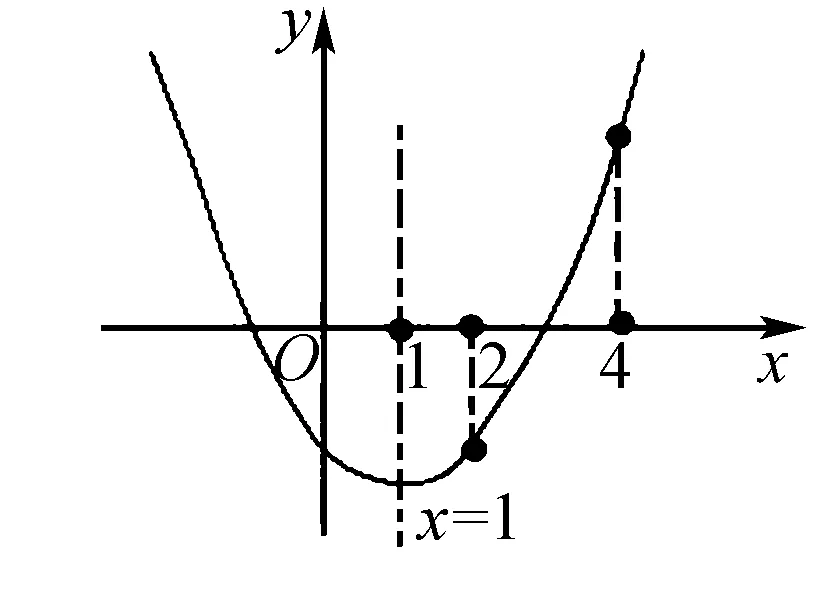
最后是符號語言與圖形語言之間的轉化.我們都知道，一次函數與二次函數都可以在坐標系中表示出來.比如學生利用學習到的數學知識，可以畫出函數f(x)=x2-2x-3的圖象，如右圖所示.

將函數關系式以圖形方式表現出來是符號語言轉化為圖形語言的典型例子，在解決高中數學問題中經常出現.提高學生符號語言與圖形語言間的轉化能力能有效提升學生的數學思維,為學生以后的發展打下良好的基礎.

3.三種語言之間的轉化

三種語言之間的轉化與兩種語言之間的轉化方法大體相同，只是在兩種語言轉化的基礎上，再將結果轉化成其它形式.三種語言之間轉化的靈活應用，能解決高中數學中的大部分問題，并且三種語言之間的轉化是在同種語言轉化與兩種語言之間的轉化基礎上進行的.教師要想引導高中學生充分利用數學問題中的關鍵信息，必須培養學生的數學語言轉化能力.促進學生數學綜合能力的提高.

綜上所述，數學語言能力是學生解決數學問題的基礎和前提，能拓展學生的解題思路，提高學生對數學問題的理解能力，在高中數學教學中，教師應采取有效的措施提高學生的數學語言轉換能力，引導學生掌握同種語言的轉化、兩種語言的轉化和三種語言之間的轉化方法.提高高中生的數學能力，為高中生的長遠發展打下良好的基礎.