微專題讓試卷講評春風拂面

江西師大附中 (330046)

黃潤華

考試是促進學生學習，檢測教學效果的有效手段.試卷講評反映教師的教學態度和教學智慧，是考試評價的核心環節，是發現并有效解決學生疑難的有效途徑.一次區域統一考試命題傾注了命題團隊大量的心血，著重考查學生的學科核心素養，所以必須科學評價考試，深入挖掘試題內涵，更加全面真實地了解學情，幫助學生查漏補缺，體會思想方法的運用，提升思維品質.教師依據試卷中的經典題、易錯題或障礙題，搜集資料，深入探究，拓展延伸，類比分析，設計有針對性的微專題課，可以讓試題講評春風拂面.

2018屆南昌市二模理科選擇題第12題，是一道根基平實、思維要求高的題.

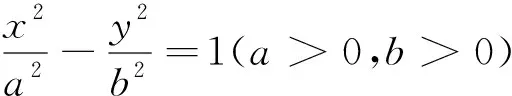
筆者以此題為核心，精心設計了一堂微專題探究課，引導學生學會分析問題，學會類比探究，學會回歸本質，學會猜想驗證，感悟觸類旁通、融會貫通的學習境界.

1.對問題解決思路的分析

先根據題意畫出草圖，在圖中標注已知條件，然后進行分析.

分析1：要求三角形AF1B內切圓的標準方程，關鍵是確定圓心的位置.

又圓心為某兩條直線的交點，已知圓心在∠AF1B的角平分線上，所以關鍵是要探究圓心還會在哪條直線上.

分析2：若從動態控制角度看，F1A,F1B可關于∠AF1B的角平分線對稱變化，交點A,B均在雙曲線上，而雙曲線的焦距已經確定，所以雙曲線只有一個參數未定，故本題中雙曲線是待定的.因此，反設雙曲線去猜想內切圓的方程不合邏輯.

分析3：除∠AF1B的角平分線外，其他條件不確定，嘗試猜想：三角形AF1B內切圓是否有什么特殊性質？其他兩個角的角平分線顯然不能得到，那么還有什么要素可以控制圓心位置呢？與內切圓圓心聯系緊密的有：過切點且與該點處的切線垂直的直線，弦的垂直平分線和內角角平分線，結合圖形去找出路.

2.對問題情境展開的聯想

通過聯想，充分運用已有的知識和方法解決新的問題，亦稱化歸思想，是人們解決問題的常用方法.本題中核心要素是雙曲線和內切圓，雙曲線的定義是隱藏條件，一般都要用到，還有三角形的內切圓滿足的性質.結合平時的學習，容易聯想到以下兩個模型：

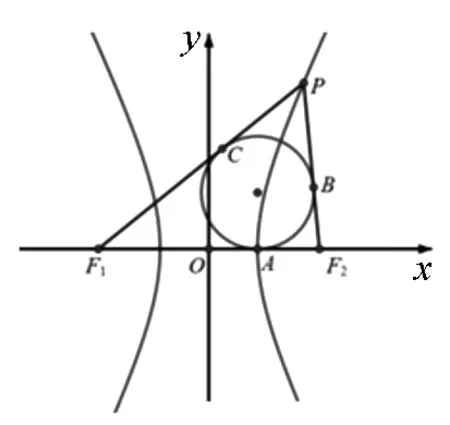
圖1

模型1 雙曲線焦點三角形的內切圓與實軸的切點是雙曲線的頂點.

證明：如圖1，|PF1|-

|PF2|=(|PC|+|CF1|)-(|PB|+|BF2|)=

|CF1|-|BF2|=|F1A|-

|AF2|=2a,又因為

|F1A|+|AF2|=2c，所以|F1A|=a+c，所以切點A為雙曲線的右頂點.

模型2 和橢圓焦點弦相切的焦點三角形的旁切圓與長軸的切點是橢圓的頂點.

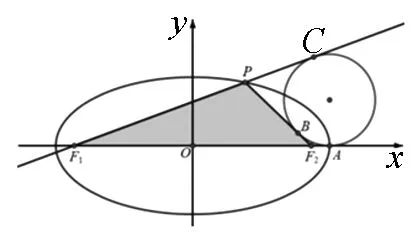
圖2

證明：如圖2，設圓切長軸于點A，切F1P的延長線于點C，則|F1C|+|F1A|=

|F1P|+|PC|+|F1F2|+

|F2A|=2c+|F1P|+

|PB|+|BF2|=2c+2a，又因為|F1C|=|F1A|，所以|F1A|=a+c，所以點A為橢圓的右頂點.

概括：第一個模型學生非常熟悉，第二個模型可能不熟悉，類比兩個模型發現，其內切圓或旁切圓均與實軸或虛軸所在直線切于曲線的頂點.

3.對問題的聯想產生的猜想

雙曲線(或橢圓)的焦點三角形的內切圓(或旁切圓)都有特定的切點——頂點，本題中不再是焦點三角形，但仍可以理解為兩個焦點三角形組合成的三角形，其依然緊密聯系圓錐曲線的定義及內切圓的有關性質，這樣我們就有理由結合草圖作出猜想:ΔAF1B的內切圓與直線AB切于右焦點F2.

要證明猜想成立，只需證明|AF2|=|AP|.根據聯想到的模型已經運用的方法可以完成證明.

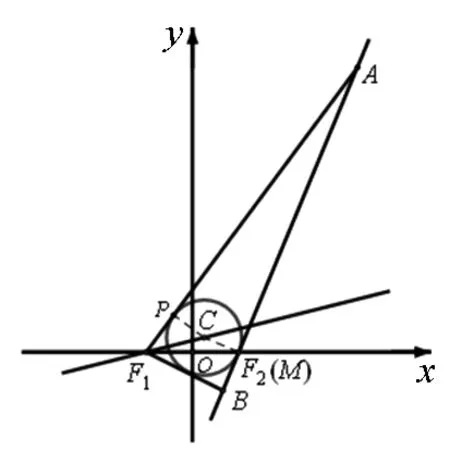
圖3

證明：如圖3，由雙曲線定義知，|AF1|-|AF2|=2a,|BF1|-|BF2|=2a.設三角形AF1B內切圓切AB于點M，則|AP|+|AM|=

|AF1|+|AF2|+|BF2|-

|BF1|=2a+2|AF2|-2a=2|AF2|，又因為|AP|=

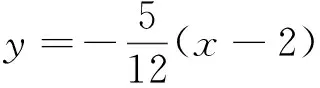
猜想是發現新問題，解決新問題的有效途徑，在教學中需培養學生良好的思維習慣，形成大膽猜想、小心求證的思維品質.本題實質上是以內切圓為背景考查切線長定理及圓錐曲線定義的靈活應用，有新穎性.

4.對問題的探究進一步拓展

教師在進行試卷講評課的設計時，為了進一步鞏固圓錐曲線定義及三角形內切圓相關性質的理解，可以搜集有關資料進行創造繼續引領學生展開探究.比如，筆者設計了如下兩道題供學生思考.

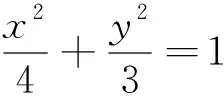
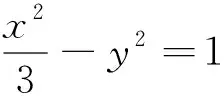
一石激起千層浪，對上述兩個問題的充分思考與交流必將激起學生濃厚的學習興趣，培養合作學習、探究拓展的思維習慣，引領學生從特殊到一般，先猜想定值的可能值，再想辦法完成一般情形的證明.

經過一番熱烈的研究與交流，同學們會驚喜地發現兩個問題中的定值均為相應曲線的離心率，回顧小結問題解決的方法，容易得出一般結論.

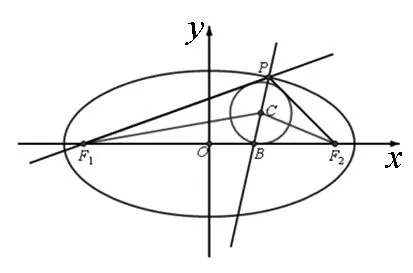
圖4

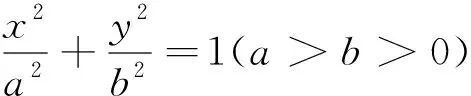
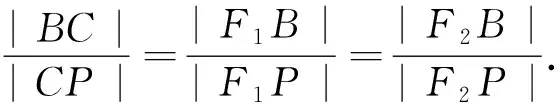
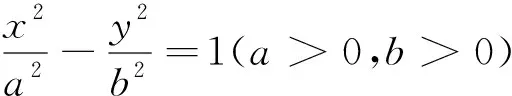
圖5

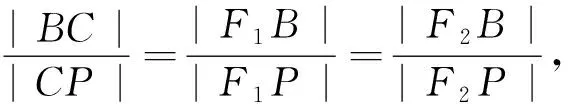
模型化思想是連通知識與應用的重要橋梁，模型化可以讓問題系統形象，對于核心的知識與思想方法，教師應創造條件使問題分門別類，讓學生觸景生情，觸類旁通.

本節微專題課經過一系列關聯問題的探究，引導學生深化對圓錐曲線定義、內心的本質特征、圓的切線有關的性質、猜想驗證和類比思想的理解與應用，有利于打通學生思維壁壘，感悟觸類旁通、融會貫通的學習境界.