教學中的“對癥下藥”

常建麗

摘 要：在我們的數學教學中經常會出現這樣的現象，老師總覺得給孩子們已經講的思路非常清晰、非常明白，但孩子們仍然不理解，不會做；有些當時會做了，過一段時間就又不會啦。我們在埋怨學生的同時，是否深究過其中原因呢？其實最根本的原因是因為在這道題中有某一個知識點，在孩子們的思維中存在困惑，搞不懂、不明白。如果你把這個癥結真正的為孩子們解開，問題也就迎刃而解了。在五年級上冊多邊形面積這一單元教學中，我就遇到了這樣的問題。

關鍵詞：教學；平行四邊形

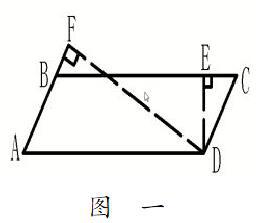
在一次單元檢測中，試卷中有這樣的一道填空題：在平行四邊形ABCD中，（如圖1）。

AB=6厘米，DF=8厘米，DE=4厘米，求平行四邊形ABCD周長是（ ）厘米，面積是（ ）平方厘米。

這道題，全班的正確率只有百分之十左右。因為是共性問題，我便在班里統一講解：要求周長，必須知道BC邊的長度，題中給出了DE 長4厘米，而DE是BC邊上的高，如果知道了平行四邊形ABCD的面積就可以用面積除以4求出BC邊的長度。而AB=6厘米，且DF=8厘米，且DF是AB邊上的高，所以用6×8可以求出平行四邊形ABCD的面積，進而再用面積除以4就算出了BC邊的長度為12厘米，進而利用（12+6）×2，就可以求出平行四邊形的周長。我自認為思路已經講的非常清晰，孩子們應該都能夠理解掌握了，但是在檢查孩子們的改錯情況時，才發現有相當一部分的答案仍然是錯的。我很郁悶，不知問題出在什么地方。于是我找過來一個孩子當面詢問，當問及是否理解、是否會做時，孩子竟然面露難色的告訴我說：老師，我沒聽懂，你說用6×8可以求出平行四邊形ABCD的面積，可是為什么呀？為什么用6×8可以求出平行四邊形ABCD的面積呢？DF和AB邊啥關系呀？我說“DF是AB邊上的高啊。”那學生就說：“為什么說DF是AB邊上的高呢？DF有一部分跑到了平行四邊形的外部，它怎么會是AB邊上的高呢？”此時我才恍然大悟，原來孩子們并不是聽不懂這類題的解題思路是什么？而是在思維深處，他不理解DF是AB邊上的高。正是因為不理解，所以孩子們在做題時很難找出二者之間的關系，當然也就無從解決問題了。此時我心里豁然開朗，知道了問題所在。看來要想真正的解決這個問題，必須讓孩子們深刻的理解，DF是AB邊上的高。于是我就在這一點上下足功夫，然后再解決問題。當時我采取了以下的教學策略：

第一步：讓學生從定義中理解什么是平行四邊形的高。（從平行四邊形一條邊上的一點到它的對邊引一條垂線，這點和垂足之間的線段叫做平行四邊形的高，垂足所在的邊叫做平行四邊形的底。）

第二步：練習畫平行四邊形兩種不同的高（如圖2）。

第三步：我把平行四邊形進行變形再變形，讓孩子們畫平行四邊形兩種不同的高。讓孩子們親身經歷當平行四邊形傾斜足夠角度時，高會出現一部分在外部的現象（如圖3）。

第四步：再講這道題，讓孩子們自己說DF是什么？那么這個題的思路應該怎么做。

經過這一番處理，孩子們才算真正明白了這個題的解題思路，也才達到了真正的理解掌握。看來孩子們之所以認為這道題比較難，不是不會分析，而是對這種特殊不常見的高沒有一個清醒和深刻的認識。在教學中，如果我們把孩子們心中的困惑真正的給他抽絲撥繭，理清楚，有針對性的去講解，對癥下藥，可能會事半功倍。反之老師講到黔驢技窮，孩子們仍然是一頭霧水。

由此可見，我們在實際教學中，不要盲目的去給孩子們講題，而是要先做調查分析，找到孩子們的困惑點在哪里，解決了困惑，難題也就迎刃而解了。