網(wǎng)絡(luò)便利樣本的推斷問題研究
王 俊,金勇進(jìn),司亞娟
(1.中國(guó)人民大學(xué)a.統(tǒng)計(jì)學(xué)院;b.應(yīng)用統(tǒng)計(jì)科學(xué)研究中心,北京100872;2.威斯康星大學(xué)麥迪遜分校生物統(tǒng)計(jì)及醫(yī)療信息系,美國(guó) 威斯康星州 WI 53726)
0 引言
隨著人們生活節(jié)奏的加快、對(duì)信息安全的擔(dān)憂等因素的影響,傳統(tǒng)的概率抽樣的回答率持續(xù)降低、花費(fèi)越來越高,并且任何試圖增加回答率的措施的單位成本也急劇上升。隨著回答率的持續(xù)降低,研究人員不得不開始懷疑這些概率樣本的代表性。與此同時(shí),隨著互聯(lián)網(wǎng)的發(fā)展,網(wǎng)絡(luò)便利調(diào)查成為了一種更為便捷、快速、便宜的收集調(diào)查數(shù)據(jù)的方式,常見的網(wǎng)絡(luò)便利調(diào)查包括自我選擇式網(wǎng)絡(luò)調(diào)查、網(wǎng)絡(luò)志愿樣本池調(diào)查。
自我選擇式網(wǎng)絡(luò)調(diào)查中,調(diào)查研究人員直接將問卷的鏈接在各大互聯(lián)網(wǎng)平臺(tái)貼出,由上網(wǎng)的人群中感興趣的網(wǎng)民自行選擇參與調(diào)查。而對(duì)于網(wǎng)絡(luò)志愿樣本池調(diào)查來說,研究人員首先通過各種方式招募(通常為非概率抽樣方法)大量的志愿者組建網(wǎng)絡(luò)志愿樣本池,當(dāng)需要進(jìn)行市場(chǎng)調(diào)研或者民意監(jiān)測(cè)時(shí),則根據(jù)一定的概率抽樣設(shè)計(jì)從網(wǎng)絡(luò)志愿樣本池中抽取一個(gè)隨機(jī)樣本。
這類基于非概率抽樣方法的網(wǎng)絡(luò)便利調(diào)查,在獲取樣本單元的過程中并不依靠特定的抽樣設(shè)計(jì),而以招募受訪者的便捷性考慮為主,通常情況下,能夠在短時(shí)間內(nèi)以較低的費(fèi)用獲取大量的樣本單元。但對(duì)這類網(wǎng)絡(luò)便利樣本而言,由于最終樣本是網(wǎng)絡(luò)總體單元自我選擇參與網(wǎng)絡(luò)調(diào)查的結(jié)果,調(diào)查研究人員無法控制整個(gè)樣本選擇的過程,因此無法像概率抽樣設(shè)計(jì)那樣計(jì)算樣本單元包含概率,進(jìn)而不能直接在基于設(shè)計(jì)的推斷框架下外推至總體。然而基于設(shè)計(jì)的推斷方法由于其簡(jiǎn)單、方便、易操作而得到的廣泛的應(yīng)用,所以如何估計(jì)網(wǎng)絡(luò)便利樣本的包含概率則是對(duì)網(wǎng)絡(luò)樣本單元進(jìn)行過推斷的一個(gè)非常重要研究方面。
Rosenbaum(1987)[1]考察了傾向得分方法在非隨機(jī)樣本統(tǒng)計(jì)推斷中的應(yīng)用,在其背景中,傾向得分解釋為總體中的單元被選進(jìn)入非隨機(jī)樣本的概率,并將估計(jì)出的傾向得分的倒數(shù)作為非隨機(jī)樣本單元的權(quán)數(shù),進(jìn)而構(gòu)建有限總體的HT估計(jì)量。在網(wǎng)絡(luò)便利樣本的推斷中,由于無法獲取總體單元層面所有的輔助信息,通常利用參照樣本來估計(jì)總體中的單元被選入網(wǎng)絡(luò)便利樣本的概率,即傾向得分。參照樣本可以是現(xiàn)存的質(zhì)量更高的概率樣本,或與網(wǎng)絡(luò)便利調(diào)查同期執(zhí)行的、質(zhì)量更高的、至少包含用于構(gòu)建傾向得分模型的變量信息的隨機(jī)電話撥號(hào)調(diào)查。
Terhanian(2000)[2],Lee(2006)[3],Lee(2009)[4]將電話隨機(jī)撥號(hào)調(diào)查獲取的樣本作為參照樣本,并將其和網(wǎng)絡(luò)便利樣本融合成一個(gè)樣本。合并后的樣本中,網(wǎng)絡(luò)樣本單元的指示變量為1,參照樣本單元?jiǎng)t為0,通過簡(jiǎn)單邏輯回歸估計(jì)出單元的傾向得分。這些方法在估計(jì)傾向得分的過程中,直接忽略了參照樣本單元的設(shè)計(jì)權(quán)數(shù)。此時(shí),利用逆傾向得分構(gòu)建的網(wǎng)絡(luò)便利樣本單元的權(quán)數(shù),只能將網(wǎng)絡(luò)便利樣本還原到合并后的樣本,估計(jì)出的傾向得分只能解釋為合并后樣本中的單元被選入至網(wǎng)絡(luò)便利樣本中的概率,而非待研究的目標(biāo)總體的單元被選入網(wǎng)絡(luò)便利樣本中的概率。Valliant(2011)[5]進(jìn)一步探討了逆傾向得分在構(gòu)建網(wǎng)絡(luò)樣本池調(diào)查樣本單元權(quán)數(shù)中的應(yīng)用,通過實(shí)證研究和嚴(yán)格的數(shù)學(xué)證明,認(rèn)為在利用參照樣本和網(wǎng)絡(luò)樣本池樣本估計(jì)傾向得分的過程中,需要將二者樣本單元的權(quán)數(shù)考慮進(jìn)邏輯回歸模型的估計(jì)過程,形成加權(quán)的邏輯回歸,并且將網(wǎng)絡(luò)樣本單元從參照樣本的抽樣框中剔除,否則將會(huì)導(dǎo)致估計(jì)量的偏差。然而在調(diào)查實(shí)踐中,如果參照樣本是現(xiàn)存
的高質(zhì)量的概率調(diào)查,則對(duì)于普通的數(shù)據(jù)使用者來說,通常無法獲取全國(guó)層面的抽樣框,即使存在全國(guó)個(gè)人層面的抽樣框,由于隱私問題,也無法獲取參與調(diào)查者的身份識(shí)別信息,因此Valliant(2011)[5]提出的方法在實(shí)際操作中將存在困難;此外,其估計(jì)出的傾向得分的實(shí)際含義也模糊不清。本文在參照樣本的背景下,考察如何利用逆傾向得分構(gòu)建網(wǎng)絡(luò)便利樣本的權(quán)數(shù),以對(duì)目標(biāo)總體的特征進(jìn)行統(tǒng)計(jì)推斷,并在Valliant(2011)[5]提出的方法的基礎(chǔ)上,將通過設(shè)計(jì)權(quán)數(shù)還原后得到的參照樣本作為“偽總體”,并基于k最近鄰的方法將網(wǎng)絡(luò)便利樣本單元從“偽總體”中剔除,此時(shí),網(wǎng)絡(luò)便利樣本則可以看成是來自“偽總體”的一個(gè)樣本,并通過加權(quán)的邏輯回歸估計(jì)出傾向得分,估計(jì)出的傾向得分則可以解釋為“偽總體”中的單元被選入至網(wǎng)絡(luò)便利樣本的概率,并將估計(jì)出的傾向得分的倒數(shù)作為網(wǎng)絡(luò)便利樣本單元的權(quán)數(shù)。
1 傾向得分及其在非隨機(jī)樣本推斷中的應(yīng)用
傾向得分方法是由Rosenbaum(1983)[6]在觀測(cè)研究中為了有效估計(jì)治療效應(yīng)而提出的方法,在此背景中,傾向得分為觀測(cè)樣本單元在給定協(xié)變量X條件下,接受治療T=1的概率 πi=P(Ti=1|Xi;γ),當(dāng) πi滿足下列條件(1)、(2)時(shí):
(1)?yi,P( )Ti=1|xi,yi;γ=P(Ti=1|xi;γ)
(2)?vi,0 < πi=P( )Ti=1|xi;γ<1
則稱單元進(jìn)入治療組或者控制組的分配機(jī)制為強(qiáng)可忽略的,即在給定X的條件下,觀測(cè)樣本單元被分配到治療組T=1還是控制組T=0是完全隨機(jī)的,和待研究變量y不相關(guān),且均有一個(gè)非0的概率被分配到治療組。此時(shí),平均治療效應(yīng)(ATE)的估計(jì)為:
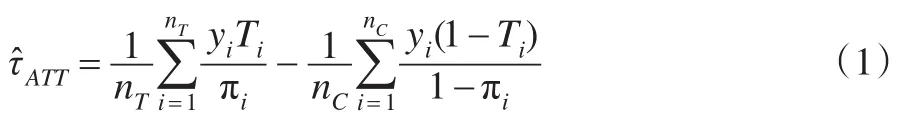
通常情況下πi的值是未知的,可以通過Logistic回歸或Probit回歸估計(jì)后帶入式(1),進(jìn)而得到。其實(shí)質(zhì)則是分別利用治療組和控制組的樣本構(gòu)造HT估計(jì)量,以估計(jì)樣本層面的待研究變量的特征,二者的差異則為樣本層面的治療效應(yīng)。在抽樣調(diào)查的背景下,P(T=1|X;γ)則稱為樣本選擇機(jī)制,T=1則目標(biāo)總體中的單元被選入至樣本,表示總體中的單元被選入樣本的包含概率。
Rosenbaum(1987)[1]探討了利用傾向得分對(duì)非隨機(jī)樣本s進(jìn)行結(jié)構(gòu)調(diào)整的方法,并假設(shè) πi=P(i∈s|Xi;γ),i∈U為總體U中的單元被選入樣本的包含概率。通過Logistic回歸估計(jì)出參數(shù)γ?,進(jìn)而得到估計(jì)出的傾向得分,進(jìn)而形成類似于HT估計(jì)量的逆傾向得分加權(quán)估計(jì)量:

2 基于k最近鄰匹配的樣本合并方法
2.1 基于k最近鄰匹配的樣本合并方法介紹
假設(shè)參照樣本sr通過樣本單元權(quán)數(shù)di,i∈sr還原得到的總體?為偽總體,由于sr為概率樣本,因此協(xié)變量X的設(shè)計(jì)無偏估計(jì)為,?則可以看成是通過基于設(shè)計(jì)的估計(jì)過程得到的估計(jì)出的目標(biāo)總體抽樣框。網(wǎng)絡(luò)便利樣本sw,權(quán)數(shù)為(當(dāng)為網(wǎng)絡(luò)志愿樣本池調(diào)查時(shí),根據(jù)從網(wǎng)絡(luò)志愿者樣本池中抽取樣本的不同,可能不為1,自我選擇樣本則均為1)。估計(jì)網(wǎng)絡(luò)便利樣本的包含概率則近似為估計(jì)網(wǎng)絡(luò)便利樣本單元從偽總體U?中被選入至sw的概率。為了集中考察方法,本文假設(shè)參照樣本和網(wǎng)絡(luò)便利樣本均包含了協(xié)變量X的測(cè)量,且不存在模式效應(yīng),參照樣本不存在無回答、涵蓋誤差等問題。估計(jì)過程見圖1。
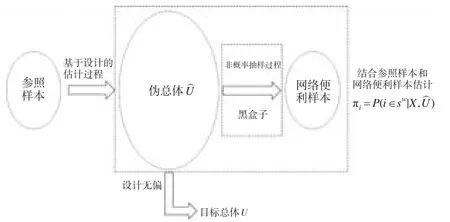
圖1 估計(jì)過程
為了估計(jì) πi=P(i∈sw|X,?),則需要將偽總體U?拆分為{?-sw,sw} 。Valliant(2011)[5]認(rèn)為應(yīng)當(dāng)將網(wǎng)絡(luò)便利樣本sw中的單元從參照樣本的抽樣框中剔除,然后將參照樣本單元的權(quán)數(shù)均乘以(其中N為目標(biāo)總體的規(guī)模)。然而在實(shí)際操作過程中,對(duì)于大多數(shù)調(diào)查人員來說,無法獲取參照樣本的總體抽樣框,因此實(shí)際應(yīng)用中存在困難,另外一方面如果參照樣本是通過復(fù)雜抽樣設(shè)計(jì)獲得的,簡(jiǎn)單將參照樣本的權(quán)數(shù)乘以將會(huì)導(dǎo)致協(xié)變量X分布的改變,更為重要的是其估計(jì)出的傾向得分的含義模糊不清。
然而在強(qiáng)可忽略的假設(shè)下,有 ?yi,P(Ii=1|xi,yi;β,γ)=P(Ii=1|xi;β),此時(shí)研究變量yi在網(wǎng)絡(luò)便利樣本sw中的分布f(yi|xi,sw;β)滿足:
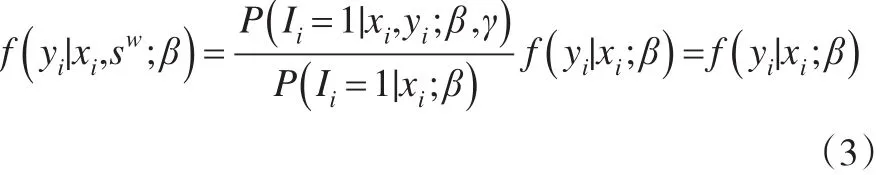
即控制了協(xié)變量Xi后,樣本中待研究變量yi在網(wǎng)絡(luò)便利樣本sw中的分布f(yi|xi,sw;β)和其在總體中的分布f(yi|xi;β)一致,如果網(wǎng)絡(luò)自愿樣本sw中的第i個(gè)單元的協(xié)變量Xi和參照樣本sr中的第j個(gè)單元的協(xié)變量Xj相同,則其待研究變量y的條件分布也相一致,此時(shí),從偽總體?中剔除一個(gè)和Xi相同的單元,則等同于將對(duì)應(yīng)參照樣本中的單元j的權(quán)數(shù)dj更新為dj-,更新后的權(quán)數(shù)不改變合并后的樣本的輔助變量X及待研究變量y在偽總體中的結(jié)構(gòu)及分布。最理想的情況是,網(wǎng)絡(luò)樣本sw中的每個(gè)單元都能夠在參照樣本sr中找到對(duì)應(yīng)的精確匹配的單元,偽總體?則拆分為{?-sw,sw}。但是實(shí)際應(yīng)用中,一方面,網(wǎng)絡(luò)樣本的樣本量通常較大,而參照樣本的樣本量通常較少,因此網(wǎng)絡(luò)樣本中的單元并不是都能夠在參照樣本中找到精確匹配的單元;其次,滿足一對(duì)一式的精確性匹配的樣本單元往往較少,如果僅使用匹配后的樣本單元,將會(huì)造成網(wǎng)絡(luò)樣本單元的大量浪費(fèi);此外,如果使用1最近鄰的方法進(jìn)行匹配通常會(huì)受到異常值的影響,尤其是當(dāng)參照樣本和網(wǎng)絡(luò)樣本之間協(xié)變量分布存在較大差異的時(shí)候。因此,本文基于kNN方法提出基于距離的加權(quán)的權(quán)數(shù)調(diào)整及樣本插入的方法,過程如下所示:
步驟1:計(jì)算距離函數(shù),并選擇最近鄰的k個(gè)單元。假如sw中第i個(gè)單元根據(jù)協(xié)變量Vi在參照樣本sr中的k最近鄰單元集合為Ni,k:

其中d(Vi,Vj)為距離函數(shù),本文選擇歐氏距離。
步驟2:?jiǎn)卧迦爰皺?quán)數(shù)更新。由于本文中原始網(wǎng)絡(luò)樣本單元的權(quán)數(shù)為,對(duì)于網(wǎng)絡(luò)樣本中第i個(gè)單元在參照樣本中的k個(gè)鄰近單元Ni,k中的第c個(gè)單元(參照樣本中的第j個(gè)單元)的權(quán)數(shù)dj更新為:
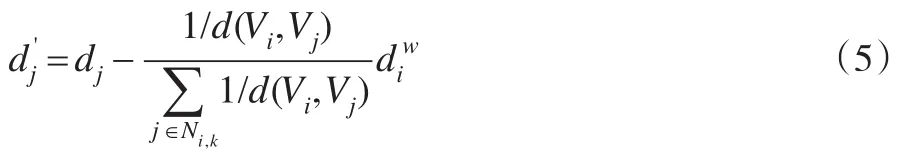
此時(shí),Ni,k中的k個(gè)單元更新后的權(quán)數(shù),(j∈Ni,k)的和為:

網(wǎng)絡(luò)樣本中的第i個(gè)單元,則相應(yīng)地插入到參照樣本中,權(quán)數(shù)為,則第i個(gè)單元的網(wǎng)絡(luò)樣本單元的權(quán)數(shù)和Ni,k中的k個(gè)單元的權(quán)數(shù)和為即參照樣本和非概率網(wǎng)絡(luò)樣本融合后,不改變?cè)紖⒄諛颖締卧獧?quán)數(shù)和。
步驟2的實(shí)質(zhì)是將網(wǎng)絡(luò)樣本單元的權(quán)數(shù)按比例從其在參照樣本中最近鄰的k個(gè)單元的原始權(quán)數(shù)dj中扣除。重復(fù)步驟1和步驟2,直到所有的網(wǎng)絡(luò)樣本單元均被插入?yún)⒄諛颖尽t最終合并后的樣本單元s={sr',sw},相應(yīng)的權(quán)數(shù)為
根據(jù)步驟2,可以得到最終合并后樣本s中單元的權(quán)數(shù)有:

即通過權(quán)數(shù)可以將合并后的樣本集合在規(guī)模上依然還原至目標(biāo)總體U。
步驟3:令I(lǐng)i=1,i∈s表合并后樣本s中第i個(gè)單元屬于網(wǎng)絡(luò)樣本sw,Ii=0,i∈s表合并后樣本s中第i個(gè)單元屬于網(wǎng)絡(luò)樣本sr'。使用加權(quán)邏輯回歸估計(jì)合并后樣本s中單元被選入網(wǎng)絡(luò)樣本sw的概率π?i。則網(wǎng)絡(luò)樣本單元的權(quán)數(shù)為wi=1,總體均值的估計(jì)為:

2.2 最近鄰匹配個(gè)數(shù)k的選擇
根據(jù)模擬的結(jié)果發(fā)現(xiàn),步驟1中隨著最近鄰匹配個(gè)數(shù)k的增加,的相對(duì)偏差(定義見式(14)),隨著k的增加不斷減小,并最終趨向于穩(wěn)定,的標(biāo)準(zhǔn)差(定義見式(10))、離散系數(shù)(CV)隨著k的增加先增加后減小并趨向穩(wěn)定。以上述模擬過程中的一次為例(如圖2),隨著k的增加估計(jì)量的相對(duì)偏差的絕對(duì)值變化相對(duì)較小,當(dāng)k=2 時(shí),估計(jì)量的相對(duì)偏差、CV最小,因此,本文中選擇使得的標(biāo)準(zhǔn)差或者CV最小的k。

圖2 最近鄰個(gè)數(shù)k的選擇
2.3 估計(jì)量的方差估計(jì)

的方差的估計(jì)為:
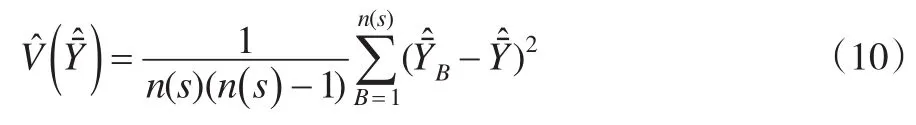
3 模擬研究
由于不同的調(diào)查模式之間會(huì)存在模式效應(yīng),比如紙筆調(diào)查和網(wǎng)絡(luò)調(diào)查、電話調(diào)查和網(wǎng)絡(luò)調(diào)查等,為了消除這種模式效應(yīng),并集中于研究不同傾向得分權(quán)數(shù)調(diào)整方法在網(wǎng)絡(luò)自愿樣本推斷中的效果,在本文的模擬研究中,使用2014年中國(guó)家庭追蹤調(diào)查(CFPS)的成人調(diào)查數(shù)據(jù),刪除個(gè)案缺失數(shù)據(jù),及對(duì)相關(guān)變量進(jìn)行隨機(jī)插補(bǔ)后,一共有14039個(gè)個(gè)案,其中可以上網(wǎng)的個(gè)案有4084人,不可以上網(wǎng)的有9955人。為了減少抽樣比較高引起的高估估計(jì)量效率的影響,本文利用有放回式的簡(jiǎn)單隨機(jī)抽樣從14039個(gè)個(gè)案中抽取1000000次,每次抽取一個(gè)單元,并將這1000000個(gè)個(gè)案作為模擬總體U。中國(guó)家庭追蹤調(diào)查(CFPS)是由北京大學(xué)社會(huì)科學(xué)調(diào)查中心組織的旨在了解中國(guó)社會(huì)、家庭及個(gè)人發(fā)展的全國(guó)性的概率調(diào)查,每年進(jìn)行一起。在CFPS的問卷中,他們?cè)O(shè)計(jì)了一個(gè)問題可以識(shí)別出樣本單元是否上網(wǎng),因此,使用CFPS的數(shù)據(jù)可以方便本文問題的研究。此外,本文通過對(duì)模擬總體數(shù)據(jù)進(jìn)行逐步回歸選取了所在省份prov、地區(qū)類型urban、年齡age、性別gender、受教育年限eduy、戶籍類型qa作為解釋總體單元能不能上網(wǎng)的協(xié)變量,并為每個(gè)模擬總體U中的單元模擬了三個(gè)連續(xù)性變量x1,x2,x3,三個(gè)變量分別來至于均值為10,5,40,方差為9,9,9的正態(tài)總體,并將上述9個(gè)變量作為估計(jì)傾向得分的解釋變量,待研究的變量y由下面的模型生成:
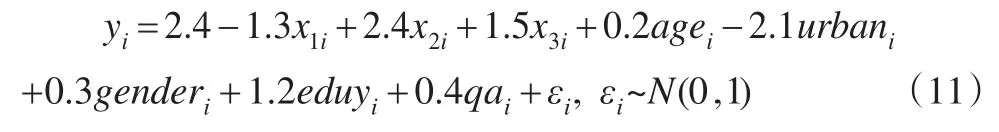
3.1 模擬過程
步驟1:利用無放回式簡(jiǎn)單隨機(jī)抽樣從總體U中抽取一個(gè)樣本量為nr的參照樣本;
步驟2:從總體U中可以上網(wǎng)的子總體UW中根據(jù)指定的樣本選擇機(jī)制:

抽取樣本量nw的網(wǎng)絡(luò)自愿樣本,其中=1表示子總體UW中第i個(gè)單元被選入到樣本,假定非概率網(wǎng)絡(luò)樣本的樣本選擇機(jī)制為L(zhǎng)ogistic形式:

步驟3:對(duì)于特定的參照樣本和網(wǎng)絡(luò)樣本的樣本量組合nr,nw,重復(fù)步驟1和步驟2抽樣過程1000次,每一次抽樣過程后,均計(jì)算以下估計(jì)量:
(1)將基本人口信息變量省份、地區(qū)類型、年齡、性別、受教育年限及戶籍類型作為輔助變量產(chǎn)生線性校準(zhǔn)估計(jì)量
(2)將式(8)中的所有變量作為輔助變量產(chǎn)生線性校準(zhǔn)估計(jì)量
(3)忽略參照樣本單元權(quán)數(shù)的簡(jiǎn)單邏輯回歸得到的逆傾向得分加權(quán)估計(jì)量
(4)Valliant提出的加權(quán)邏輯回歸得到的逆傾向得分估計(jì)量
(5)本文提出的逆傾向得分加權(quán)估計(jì)量
本文從平均相對(duì)偏差(R.Bias)、平均標(biāo)準(zhǔn)差(S.E)及95%置信區(qū)間包含真值的比例(Coverage rate)三個(gè)方面對(duì)不同的估計(jì)量進(jìn)行比較。
平均相對(duì)偏差定義為:
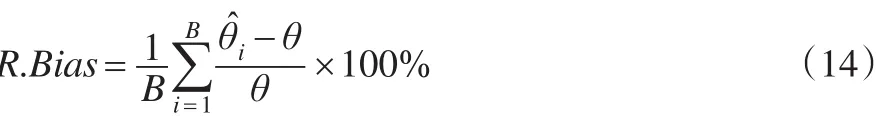
其中B為對(duì)于每次實(shí)驗(yàn)過程重復(fù)的次數(shù),本文中B=1000,?為第i次實(shí)驗(yàn)得到的總體特征的估計(jì),θ為總體特征真值。
平均標(biāo)準(zhǔn)差定義為:
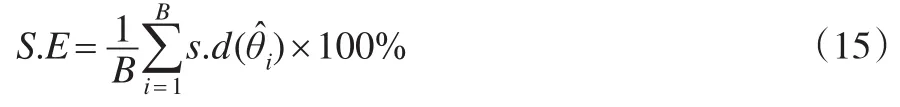
其中為第i次重復(fù)實(shí)驗(yàn)得到的估計(jì)量的標(biāo)準(zhǔn)差。
95%置信區(qū)間包含真值的比例定義為:

其中Interval為第i次模擬過程構(gòu)造的置信區(qū)間。
步驟4:為了研究不同樣本量nr,nw對(duì)估計(jì)結(jié)果的影響,本文賦予nr,nw不同的樣本量組合,如表1所示:
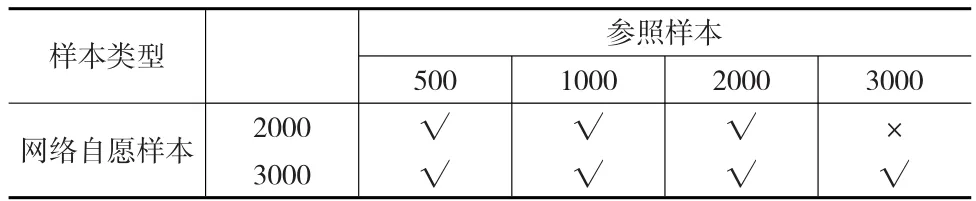
表1 不同的樣本組合
表中“√”表示有效的實(shí)驗(yàn)組合,“×”表示本文未做該樣本組合的模擬研究。相比較于網(wǎng)絡(luò)調(diào)查,傳統(tǒng)的概率抽樣花費(fèi)較為昂貴,因此在本文的模擬研究中,限定參照樣本的樣本量不多于網(wǎng)絡(luò)自愿樣本的樣本量。對(duì)于不同的nr和nw,重復(fù)步驟1至步驟3。
3.2 結(jié)果
從表2(見下頁(yè))可以看到,估計(jì)傾向得分模型時(shí),如果忽略參照樣本的設(shè)計(jì)權(quán)數(shù),直接利用簡(jiǎn)單邏輯回顧,則得到的逆傾向的分加權(quán)估計(jì)量平均相對(duì)偏差較大,均在-10%以上,當(dāng)網(wǎng)絡(luò)便利樣本量固定時(shí),隨著參照樣本量的增加,的平均相對(duì)偏差有減少的趨勢(shì),但仍高于-10%,此時(shí),網(wǎng)絡(luò)便利樣本樣本量的增加并不能有效減少此估計(jì)量的平均相對(duì)偏差;Valliant提出的使用參照樣本的設(shè)計(jì)權(quán)數(shù),通過加權(quán)Logistic回歸得到的逆傾向得分估計(jì)量以及本文提出的基于kNN的樣本合并方法得到的逆傾向得分估計(jì)量的平均相對(duì)偏差較小,均在5%以內(nèi),當(dāng)網(wǎng)絡(luò)便利樣本的樣本量為2000時(shí),兩種估計(jì)量的相對(duì)偏差幾乎相同,網(wǎng)絡(luò)便利樣本的樣本量增加到3000時(shí),的平均相對(duì)偏差均小于。
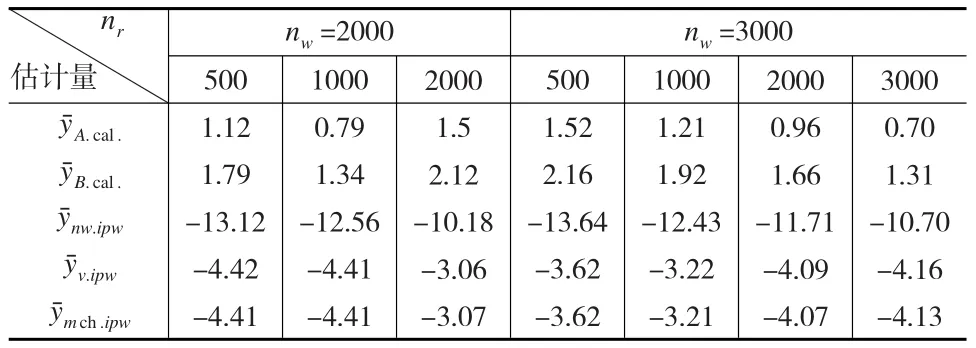
表2 不同樣本組合下估計(jì)量相對(duì)偏差R.Bias結(jié)果
從95%的置信區(qū)間包含真值比例方面來看(見表3),的95%的置信區(qū)間包含真值的比例較低,在本文的模擬研究中均不高于90%;及95%的置信區(qū)間包含真值的比例均接近95%,當(dāng)網(wǎng)絡(luò)便利樣本的樣本量固定時(shí),隨著參照樣本量的增加,兩種估計(jì)量的95%置信區(qū)間包含真值的比例,有微弱的下降趨勢(shì),比如當(dāng)網(wǎng)絡(luò)樣本量為3000時(shí),隨著參照樣本量從500增加到3000,的95%置信區(qū)間包含真值的比例由95.1%下降至93.9%。
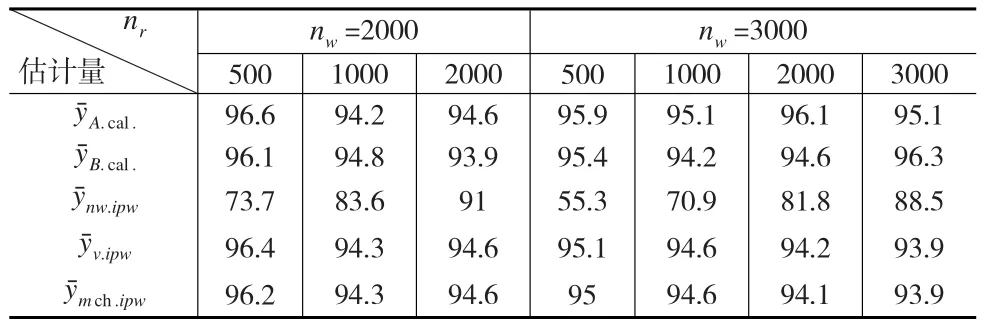
表3 不同樣本組合下估計(jì)量95%置信區(qū)間C.Rate結(jié)果
從平均標(biāo)準(zhǔn)差SE來看,在網(wǎng)絡(luò)便利樣本的樣本量固定的條件下,隨著參照樣本的增加(見表4),及的標(biāo)準(zhǔn)差逐漸減少,而對(duì)于忽略樣本單元權(quán)數(shù)的簡(jiǎn)單邏輯回歸得到的逆傾向得分加權(quán)估計(jì)量卻有增加的趨勢(shì)。
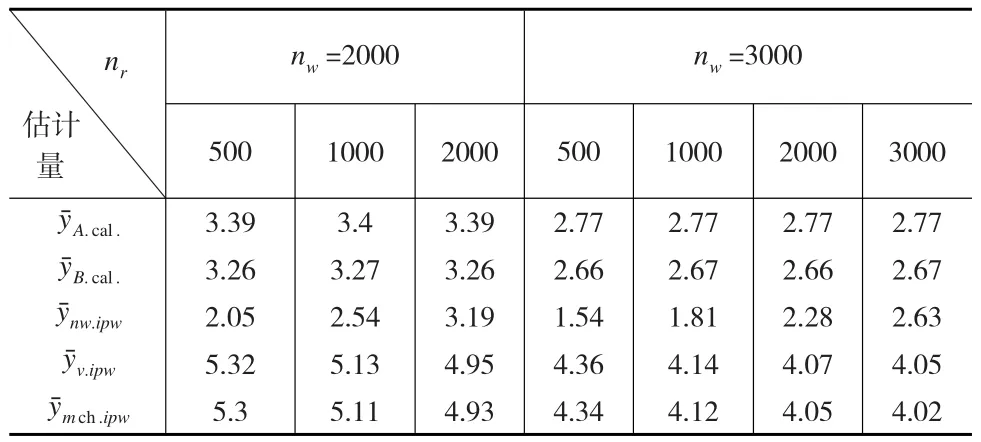
表4 不同樣本組合下估計(jì)量標(biāo)準(zhǔn)差SE結(jié)果
值得注意的是,當(dāng)校準(zhǔn)變量為生成y的模型中所有變量時(shí)或者部分人口信息變量時(shí),校準(zhǔn)估計(jì)能夠顯著減少估計(jì)量的偏差,但不能完全消除偏差。然而校準(zhǔn)變量的選擇必須與待研究變量高度相關(guān)才能達(dá)到減少估計(jì)量偏差的效果,本文中選擇的校準(zhǔn)變量為生成待研究變量模型中的一部分或者全部,因此校準(zhǔn)估計(jì)的模擬結(jié)果與其他方法相比具有較高的效率。
4 結(jié)論
本文在網(wǎng)絡(luò)便利樣本的背景下,介紹了傾向得分及其在利用網(wǎng)絡(luò)便利樣本對(duì)目標(biāo)總體進(jìn)行推斷中的應(yīng)用,并提出了基于k-NN的樣本合并方法及相應(yīng)的逆傾向得分估計(jì)量。模擬結(jié)果表明在估計(jì)傾向得分模型時(shí),如果不考慮樣本單元的權(quán)數(shù),構(gòu)建的逆傾向得分估計(jì)量的偏差相對(duì)較大、95%置信區(qū)間包含比例也較低;本文提出的基于k-NN樣本合并方法及對(duì)應(yīng)的逆傾向得分估計(jì)量,與Valliant提出的方法相比,在實(shí)際使用過程中,具有更高的操作性,且當(dāng)網(wǎng)絡(luò)便利樣本的樣本量較大時(shí),能夠相對(duì)減少估計(jì)量的偏差。此外,相對(duì)于利用傾向得分構(gòu)建權(quán)數(shù)的方法,當(dāng)將生成待研究變量y的所有協(xié)變量都包含進(jìn)校準(zhǔn)模型時(shí),校準(zhǔn)估計(jì)的平均偏差最小,隨著樣本量的增加平均偏差趨向于0。當(dāng)校準(zhǔn)模型中只包含基本的人口信息變量時(shí),雖然相對(duì)于未截取的逆傾向得分估計(jì)量有所減低,但不能完全消除偏差。

