基于一般灰數的廣義灰色關聯分析模型

蔣詩泉，劉思峰，劉中俠，方志耕

（1.銅陵學院 數學與計算機學院，安徽 銅陵 244000；2.南京航空航天大學 經濟與管理學院，南京 210016）

0 引言

灰色關聯分析是一種因素分析方法，灰色關聯度模型是灰色關聯決策理論的重要基礎，是分析不確定性系統的一個重要的工具。鄧聚龍第一次使用歐式距離來測度兩個系統在發展趨勢上的相似性，并提出了關聯系數的概念和灰色關聯度一般模型[1，2]。在此基礎上，文獻[3-5]從關聯系數、序列之間距離的測度等不同角度對灰色關聯度進行了改進與拓展研究，對新型灰色關聯度模型的構建進行有益的探索。受關聯度構造思想的影響，劉思峰提出灰色絕對關聯度和灰色相對關聯度模型[6-8]。在分析前期提出的關聯度模型存在問題及其原因基礎上，從相似性和接近性兩個不同的視角測度序列之間的相互關系和影響，提出了灰色相似關聯度和灰色絕對關聯度[9]。隨著系統發展演化的復雜性，其不確定性表現的越來越普遍，對系統刻畫很難用一個實數或一個區間灰數能夠準確地描述系統發展和演化特征，為了準確描述系統的特征，劉思峰提出了一般灰數的概念。本文在一般灰數概念基礎上，基于核與灰度的思想，依廣義關聯分析模型的路徑，提出一般灰數的絕對和相對關聯度模型及相似性和接近性關聯度模型及其相應的決策模型，并給出了核期望與核方差的一般灰數的排序方法。最后，利用具有實際背景的案例驗證了所建模型在決策應用中的科學有效性。

1 一般灰數的基本概念與定義

定義1[6]：區間灰數和實（白）數統稱為灰數基元。

定義2[6]：設，則稱g±為一般灰數。其中任一區間灰數，滿足且分別稱為g±的下界和上界。

定 義 3[6]：（1）設為一般灰數，稱為g±的核。（2）設g±為概率分布已知的一般灰數，的概率為pi且滿足，則稱為g±的核。

定義 4[10]：設一般灰數的背景或論域為為 Ω 的測度，則稱為一般灰數g±的灰度。一般灰數g±的灰度也簡記為go。 其 中 ，記的 灰 度 ，且

由灰數灰度的定義可知，灰度是表征灰數用其“核”代替其真值的不確定性程度，換句話說就是表示“核”作為區間灰數的真值代表的可能性大小，即概率大小。由此得到基于灰度的一般灰數的核期望與核方差定義。

E(g±)反映了一般灰數“核”的平均水平，D(g±)反映“核”取平均值的穩定性或者各個的離散程度。

命題1：實數的灰度為零，在一般灰數的四則運算過程中參與核的運算但不參與灰度運算。

公理1：（灰度不減公理）當n個一般灰數，，…，進行加法（或減法）運算時，運算結果的灰度不小于其中最小灰度的灰數灰度，為簡單灰度取其平均值。乘法（或除法）運算時，運算結果的灰度不小于其中灰度最大的灰數灰度。

公理 2：記則一般灰數的運算法則如下：

2 一般灰數的核期望與核方差排序方法

定義7：若一般灰數核期望和核方差如定義5或定義6所示，對于一般灰數和，

3 一般灰數的廣義關聯度模型構建

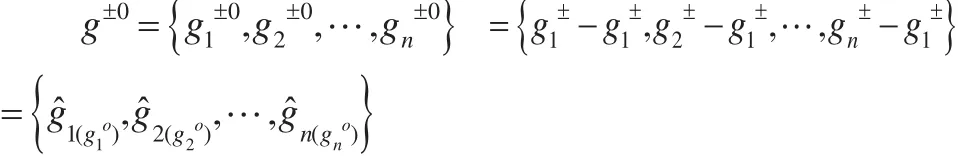
引理1：設一般灰數序列和是等長等間距序列

=，其相應的始點零化像分別為和，則：

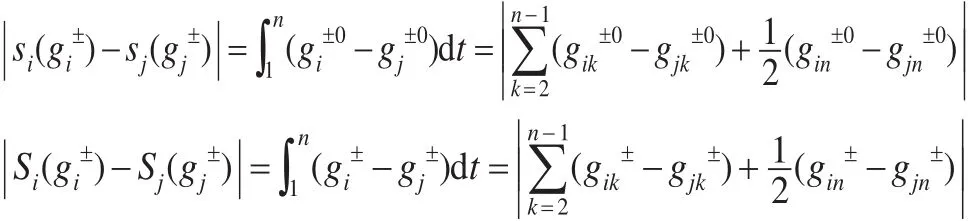
證明：由于一般灰數化為簡化形式，即實數形式，證明類似文獻[6]，具體證明過程略。

定理1：設一般灰數序列和是等長等間距序列

，其相應的始點零化像分別為和。令：

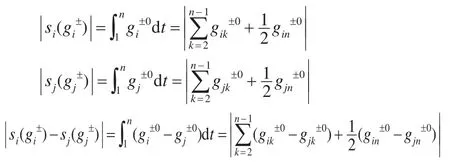
為一般灰數序列和之間的絕對關聯度。

證明：（1）規范性：顯然，εij＞0。又所以εij≤1；（2）接近性：顯然成立。

定理2：設一般灰數序列和是等長等間距序列，

，初值化像分別和其相應的始點零化像分別為和。令：

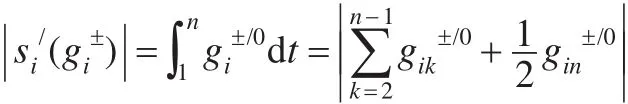
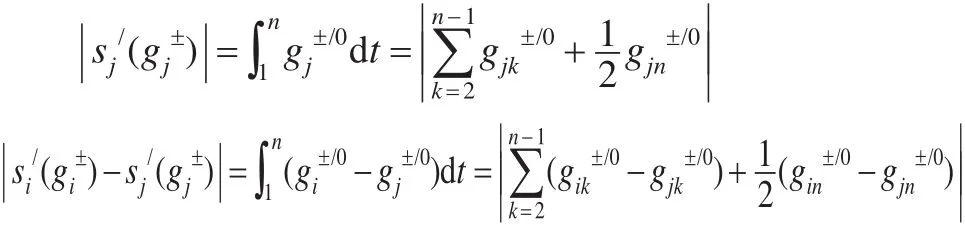
證明：類似定理1。

定義10：設一般灰數序列和是等長等間距序列，且g?1≠0 ，εij和rij分別為一般灰數序列與的絕對關聯度和相對關聯度，θ∈[0，1]，則稱ρij=θεij+(1-θ)rij為一般灰數序列與的綜合關聯度。

定理3：設一般灰數序列和是等長等間距序列，其相應的始點零化像分別為和，稱為一般灰數序列和基于相似性關聯度，簡稱為相似性關聯度。為一般灰數序列和基于接近性關聯度，簡稱為接近性關聯度。

證明：（1）規范性：顯然，αij＞0 。又≥0，所以αij≤1；（2）接近性：顯然成立。

似可以證明βij也滿足鄧氏關聯度的規范性和接近性。

4 基于一般灰數的關聯決策模型構建與步驟

步驟1：將一般灰數決策序列矩陣進行規范化處理。

skj為方案k的第j個指標為一般灰數，即其中k=1，2，…，l，j=1，2，…，m。

若skj為效益型指標，則規范化為rkj=，其中

若skj為成本型指標，則規范化為其中

步驟2：確定正、負理想方案。

（1）正理想方案

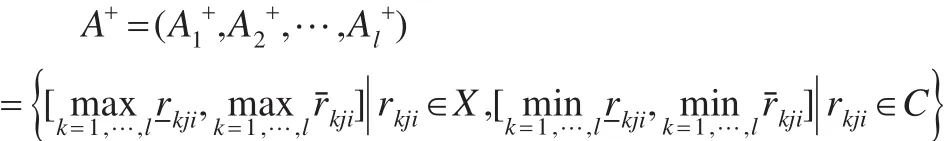
（2）負理想方案

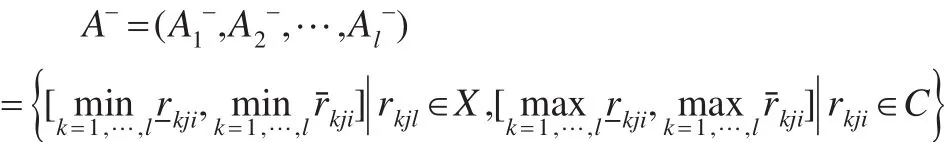
其中X,C分別表示效益型指標和成本性指標。

步驟3：將一般灰數轉化為灰數的簡化形式，即g±=形式。

步驟4：按定義8或定義9分別將一般灰數序列通過始點零化像處理為。

步驟5：按定理1和定理2計算正負理想與方案序列間絕對關聯度值和相對關聯度值。

步驟6：按定義10和定義11計算綜合關聯度值和綜合關聯貼近度值。

步驟7：按定義7對的一般灰數排序方法對方案進行排序。

5 案例分析

某投資銀行，準備對一個企業進行投資，通過第一輪篩選后，還剩最后三家企業，現要在這三家企業A1，A2，A3中選擇一家，其評價指標分別為S1：表示企業年產值（千萬元），S2:表示企業社會效益（千萬元），S3：表示對環境效率，具體指標數據見表1所示。試確定銀行的最佳投資方案。

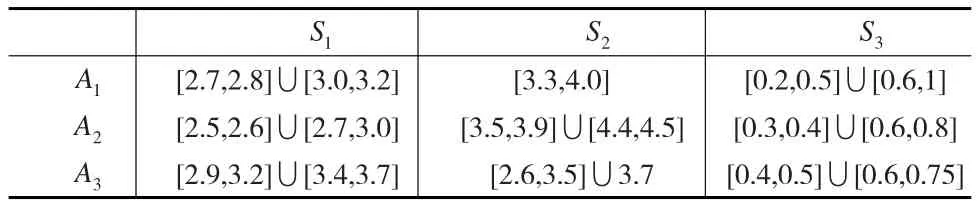
表1 決策矩陣

步驟1：將決策矩陣進行規范化處理（見表2）。

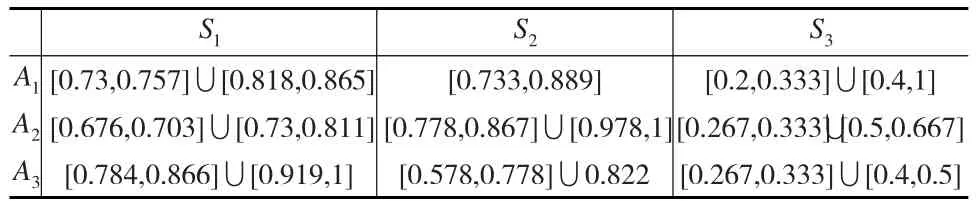
表2 規范化決策矩陣

步驟2：確定正負理想方案。

步驟3：將規范化決策矩陣表示為簡化形式的決策矩陣A,并將正負理想方案序列化為簡化形式。

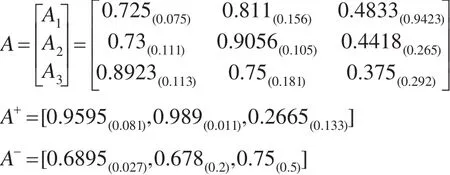
步驟4：按定義9對正負理想序列和A的每行進行始點零化像處理。

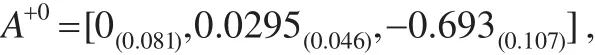
步驟5：利用定理1和定理2分別計算每個方案與正負理想方案的絕對關聯度和相對關聯度及綜合關聯度。

各方案與正理想的絕對關聯度、相對關聯度和綜合關聯度分別為：

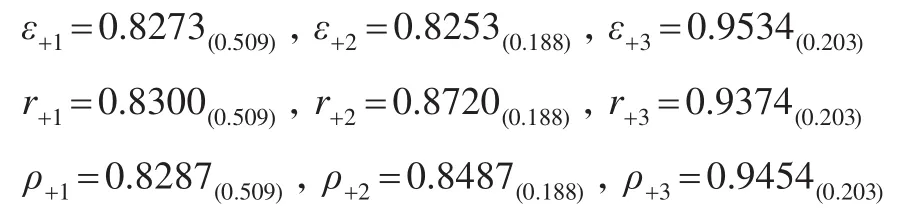
各方案與負理想的絕對關聯度、相對關聯度和綜合關聯度分別為：

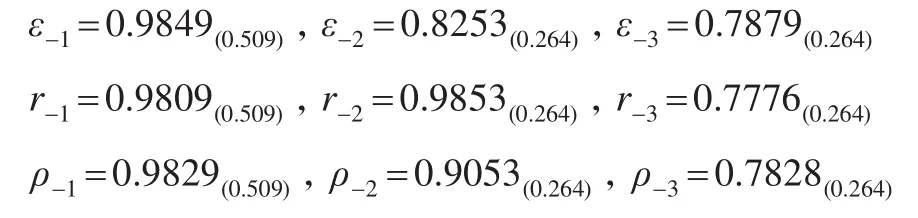
步驟6：計算綜合關聯相對貼近度。

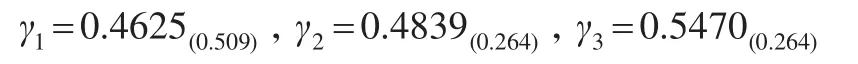
步驟7：按定義8對方案進行排序。

可以利用核與灰度的關系，將其簡化形式轉換為一般區間灰數，其中區間灰數的核期望就是簡化形式的核。故按照定義8，可以得到如下排序為：γ3?γ2?γ1。所以方案排序為A3?A2?A1，即方案A3為最優方案。即投資銀行應該給企業A3進行投資。

為了說明該決策模型的科學性和合理性，現與文獻[18]和文獻[6]進行比較。利用文獻[6]求一般灰數核，計算核的灰色綜合關聯貼近度并依其值進行方案排序。文獻[18]是基于擴展灰數Hausdorff距離的隨機準則決策方法，其決策關鍵是測度擴展灰數的距離，最后利用基于TOPSS的隨機準則的貼近度排序。具體排序見表3所示。

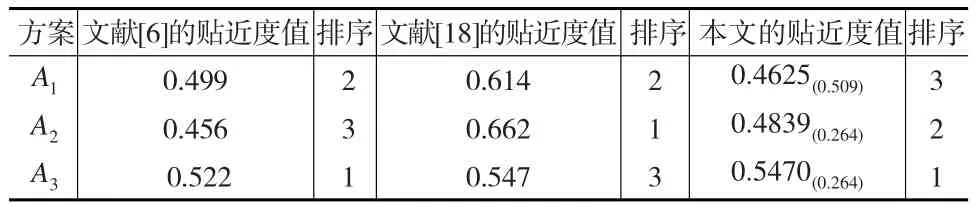
表3 不同方法排序結果比較

從表3的排序結果可以看出文獻[6]的排序同本文方法排序比較接近，由于文獻[6]在一般灰數運算時只考慮一般灰數的核而沒有考慮一般灰數的灰度，從而造成決策稍有偏差。文獻[11]的結果與本文的結果相差甚遠，主要原因在于文獻[11]中對擴展灰數距離的測度的方法上，由于目前對擴展灰數距離測度沒有一個令人滿意的解決方法，所以不同的距離測度方法都會導致不同的結果。本文最大優點是基于核與灰度為灰理論思想來處理一般灰數的運算與排序，目前來看還是極其合理的。

6 結束語

隨著系統的不確定性更為一般化，對復雜系統不確定性表征更加復雜，本文針對復雜系統信息表征為一般灰數時，提出了一種灰色絕對關聯度和灰色相對關聯度模型，該模型是現有實數型絕對關聯度模型和相對關聯度模型的拓展研究。基于核與灰度思想，提出了一般灰數的核期望與核方差的排序方法，再此基礎上研究了一般灰數的灰色關聯決策模型。本文為探討基于一般灰數的關聯度分析提供了一個新的視角和思路，克服了現有模型對一般灰數類型數據的關聯分析的不足。通過算例驗證了該模型的合理性和有效性。