火星表面大氣環境下熱球風速儀的對流換熱模型及試驗驗證

李西園，侯雅琴，高慶華，張麗娜，王 晶,3

（1. 北京衛星環境工程研究所，北京 100094； 2. 北京航空航天大學 航空科學與工程學院，北京 100191；3. 北京衛星環境工程研究所 可靠性與環境工程技術重點實驗室，北京 100094）

0 引言

火星表面大氣壓力約為700 Pa，主要成分為CO2，溫度-120～20 ℃，風速 0～15 m/s。極低氣壓環境下存在的對流換熱使火星表面巡視器面臨著與地球和一般航天器軌道空間不同的環境。為了在極端環境下達到熱模型修正、早期故障篩除、性能測試等目的，火星巡視器的地面熱試驗一般需要極端環境疊加風速模擬[1-2]，即在中型空間環境模擬設備內部，通過調溫熱沉模擬冷黑背景，調溫冷板模擬巡視器的地表傳熱，壓力控制系統模擬1400 Pa左右壓力環境，通過風機模擬最大15 m/s的風速，并需要對試驗中的風速進行實時測量。

目前工業上常用的風速測量手段主要包括動壓式、熱式和超聲式等。動壓式風速測量主要包括風杯式、皮托管和五孔探針等形式，其中皮托管和五孔探針已經被廣泛應用于低氣壓風速測量領域。在火星表面壓力下，0～15 m/s風速帶來的動壓僅有0.01～10 Pa，盡管現有微壓傳感器產品的分辨率可以達到10-3Pa，但其體積、質量往往較大，且無法在低氣壓下使用，需要使用管路在容器外進行測量，而多點風速、風向的測量將會使系統變得非常復雜[3]。熱式風速測量包括熱線、熱球和熱膜等形式，其工作原理是可根據不同風速下傳感器探頭換熱量的不同計算風速[4]。在“Netlander”“海盜號”“小獵犬二號”等火星探測器上均搭載有熱式風速儀，部分還具有通過尾跡線測量風向的能力[5-6]。熱式風速儀結構簡單緊湊、質量小、功耗低、不需要移動部件，但其缺點也很明顯：1）傳感器對標定的依賴性大，無法通過分析手段獲得信號?風速的關聯式；2）隨著時間推移，傳感器阻值等特性變化會引起標定漂移；3）空氣溫度變化會導致信號的變化，故傳感器的測量精度非常依賴于氣體溫度的測量。目前火星探測器使用的熱式風速儀均為定制產品。超聲風速測量利用了聲波信號在介質中傳播速度僅和氣體成分及溫度相關，而和壓力無關的特性。相比熱式風速儀，超聲風速儀不需要每個都標定，其主要缺點在于超聲波在低氣壓下衰減較大，現有產品往往很難從噪聲信號中篩取超聲換能器發射的信號，需要設計全新的換能器[7-8]，同時設備體積較大，難以滿足多點風速測量的要求。

綜上所述，目前在極低氣壓下，風速測量的主要途徑為定制型風速傳感器。本文主要針對在低氣壓下使用現有工業用恒熱流熱球風速傳感器的適用性，采用無量綱數分析方法建立熱球風速傳感器表面的傳熱模型，分析傳感器在不同壓力下的響應特性，并搭建試驗系統進行測試驗證。

1 熱球風速儀對流換熱模型

1.1 仿真模型

熱球風速探頭的核心為陶瓷封裝的微小球體，直徑約為0.6 mm，球體內部包括熱電偶的熱端和加熱絲，外部包括熱電偶的冷端，圖1所示為本文使用的熱球風速探頭的結構。

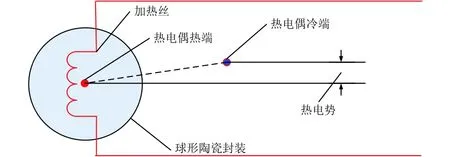
圖1 熱球風速探頭結構Fig. 1 Structure of hot-bulb anemometer probe

風速測量中，加熱絲上的恒定電流產生恒定的功率，此時，熱電偶冷端溫度可以認為是流體溫度，而熱端溫度為熱球溫度。當不同速度流體流過熱球表面時，對流換熱系數的不同導致了球表溫度的不同，繼而在熱電偶冷、熱端之間形成熱電勢差；通過毫伏變送器可以對熱電勢差進行測量、傳輸，根據傳感器的標定數據可換算出當前的風速。

1.2 無量綱數模型建立

傳感器敏感頭與周圍環境的換熱可以分為輻射換熱、對流換熱及通過引線導熱3種，當忽略沿細線上的導熱時，在熱平衡狀態下探頭的加熱量等于探頭的對外換熱量之和，

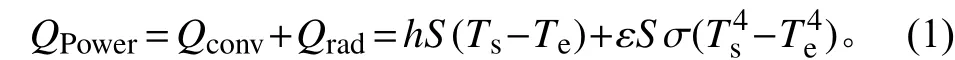
式中：Qpower為傳感器敏感頭熱耗，W；Qconv為通過對流散失的熱量，W；Qrad為通過輻射散失的熱量，W；h為對流換熱系數，W/(m2·K)；S為熱球表面積，m2；ε為熱球表面發射率；σ為斯忒藩?玻耳茲曼常量，5.67×10-8W/(m2·K4)；Ts、Te分別為熱球表面溫度和來流氣體溫度。考慮到敏感頭實際與設計尺寸的偏差及引線上損失的熱耗時，式(1)可表達為

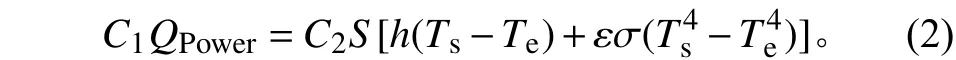
式中：C1為敏感頭上電阻在整個加熱回路電阻中的占比；C2為敏感頭實際表面積與設計表面積的比值。式(2)可以繼續簡化為

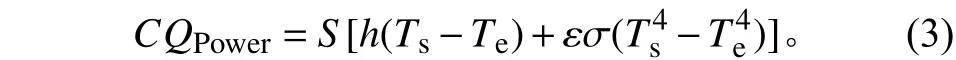
其中C為常數，包括了C1和C2兩項常數的影響，通過數據擬合得到。

式(1)～(3)中的對流換熱系數h可由努賽爾數Nu表示，

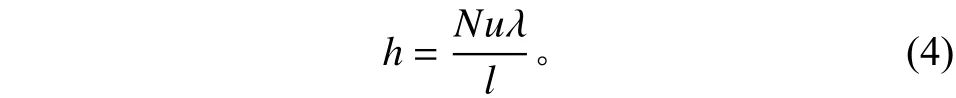
式中：λ為傳熱系數，W/(m·K)，隨氣體壓力變化不大；l為特征長度，m；Nu一般可以表示為雷諾數Re的函數。球體表面流動的雷諾數可以表示為

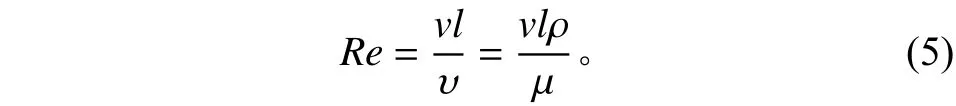
式中：v為氣體流速，m/s；l為特征長度，m，取0.000 6 m；υ為氣體的運動黏度，m2/s。υ隨氣體密度ρ變化，故將其轉換為動力黏度μ和ρ的比值，其中，動力黏度μ是不隨ρ變化的，氣體密度ρ可由理想氣體狀態方程，通過氣體壓力、溫度計算得到。根據計算，常壓、0～15 m/s風速下，Re約為20～500；而在 1400 Pa環境下，Re僅為 0.1～2。針對球體表面強制對流Nu?Re經驗關聯式，Kramers、Whitaker、Yuge、Vilet、Raithby 等學者通過試驗，給出了適用于不同范圍的表達式[9]，但大多適用于中高雷諾數，在低雷諾數（0.1～10）范圍偏差較大，不同經驗公式間偏差可達20%[10]。根據統計，Whitaker關聯式

在低雷諾數時與試驗結果最為接近，其中Pr為流體普朗特數。

若式(4)～(6)中的定性溫度均選取熱球表面溫度Ts與來流氣體溫度Te的平均值，傳熱系數λ、動力黏度μ、普朗特數Pr均表示為定性溫度的函數，則當來流氣體的溫度、速度已知時，可通過式(4)～(6)計算敏感頭表面對流換熱系數h。再將各參數代入式(3)后可求解非線性方程獲得熱球風速傳感器的表面溫度。當熱電偶的輸出信號ΔU與溫差ΔT滿足ΔU=k×ΔT關系時，即可由ΔT計算得到熱電偶輸出信號ΔU。本文試驗所用熱電偶的k約為0.041 mV/℃。

1.3 自然對流與強制對流強度分析

熱式風速儀傳感器探頭表面存在自然對流和強制對流。對于恒熱流風速探頭而言，自然對流隨著探頭的表面溫度而變化，會給測量帶來額外的誤差，故測量時應當確保探頭表面的強制對流占據主導地位。可根據無量綱數Gr/Re2來判斷強制對流或自然對流的主導地位：Gr/Re2＜0.01時強制對流占據主導地位，Gr/Re2＞10時自然對流占據主導地位，Gr/Re2在0.01～10之間時則需要同時考慮這2種對流因素的影響。

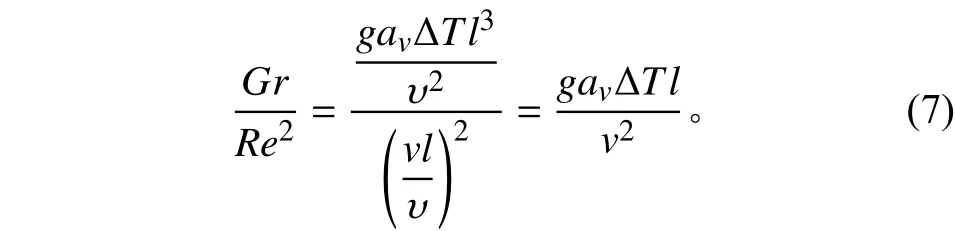
式中：Gr為格拉曉夫數；g為重力加速度，m/s2；ΔT為熱球與環境氣體間的溫差，K；av為體脹系數，K-1，其表達式為

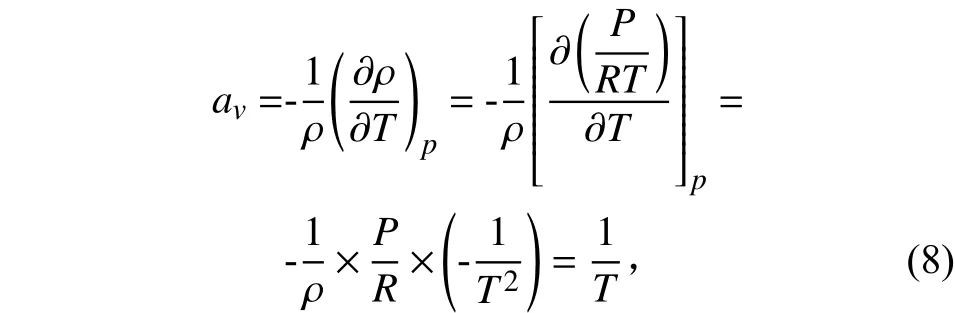
其中：ρ為氣體密度，kg/m3；P為壓力，Pa；T為定性溫度，K；R為摩爾氣體常數。可見體脹系數與壓力無關，即衡量自然對流與強制對流模式占比的無量綱數僅和重力加速度、定性溫度、來流氣體與熱球表面的溫差、特征長度、來流速度有關，其中重力加速度、特征長度、來流速度為給定值，溫差可通過1.2節方法求解獲得，定性溫度T取來流氣體與熱球表面溫度的平均值。

2 試驗驗證

2.1 試驗系統及方法

為了對無量綱數模型進行驗證，需要在地面建立低氣壓風速模擬手段。目前對于1400 Pa左右低氣壓下的風速模擬有旋轉、閉式風洞和開式風洞3種基本方法[3]。其中旋轉法的基本原理如圖2所示，旋轉的風速儀穿過流體，流體介質不運動，風速儀與流體介質之間存在相對運動。一般是把懸臂和轉臺放置于空間環境模擬容器中，容器中充入與使用環境具有相同壓力、溫度的氣體。旋轉風速模擬系統具有成本低，結構簡單，容器內壓力、氣體成分穩定的優點。

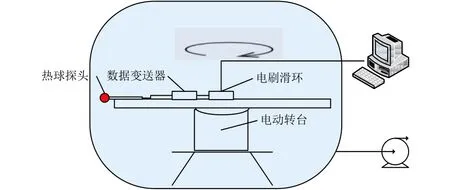
圖2 基于旋轉的風速模擬系統組成Fig. 2 Wind speed simulation system based on rotation

本文基于中型空間環境模擬設備搭建了旋轉風速模擬系統，見圖3。熱球風速探頭固定于懸臂端部，已知懸臂半徑和懸臂轉速時可知當前風速，懸臂上安裝的12位精度毫伏信號采集器可直接工作于真空環境下，采集分辨率約為0.01 mV，轉換為485信號后由轉臺上的電刷滑環導出，并傳送至容器外的計算機存儲。傳感器的恒定熱流施加使用了容器外的程控電源，功率恒為0.08 W。

圖3 風速模擬系統實物Fig. 3 Photo of the wind speed simulation system

2.2 試驗結果與分析

分別對常壓、4×104Pa、1400 Pa下的風速傳感探頭輸出進行了測試。在試驗中背景溫度與流體溫度相同，均為室溫。

2.2.1 常壓下

圖4和圖5分別為常壓下輸出信號與無量綱數方法預測的信號對比（其中擬合常數C≈0.067）及相應風速下的Gr/Re2，其中受限于懸臂在常壓下的空氣阻力，僅模擬了0～11 m/s風速下的傳感器輸出。由圖可見，在常壓下，恒熱流式熱球風速儀的無量綱數模型與實際輸出信號的吻合度非常好，偏差在0.05 mV以內。同時，無量綱數Gr/Re2均＜0.01，即熱球風速儀表面強制對流占主導地位。

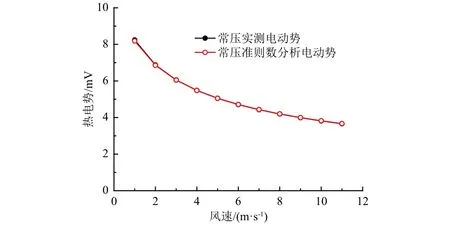
圖4 常壓下探頭輸出與無量綱分析對比Fig. 4 Comparison between probe output and dimensional analysis under ambient pressure

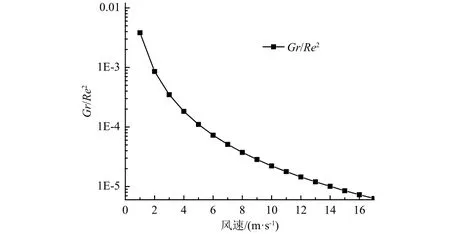
圖5 常壓不同風速下的Gr/Re2Fig. 5 Gr/Re2 at different wind speeds under ambient pressure

2.2.2 低壓下

繪制4×104Pa、1400 Pa下傳感器輸出與無量綱數模型分析結果的對比（見圖6）。在4×104Pa下，二者數值較為接近，但在1400 Pa壓力下，分析值與試驗輸出存在較大的偏差，這與文獻[11]中針對熱線風速儀的試驗結果是一致的，即在極低氣壓下，Nu?Re關聯式會隨壓力的降低產生較大的偏差。因此，對于低氣壓下的熱式風速儀的適用性研究，需要結合試驗數據進行修正。

圖6 4×104 Pa與1400 Pa下探頭輸出與無量綱分析對比Fig. 6 Comparison of probe output and Gr/Re2 analysis under pressures of 4×104 Pa and 1400 Pa

同時，由圖6可見，在1400 Pa下，傳感器在不同風速下的靈敏度約為0.1～0.2 mV/(m·s-1)；在低氣壓下進行風速測量試驗時，毫伏信號的數據采集器亦應當滿足相應的精度要求。此外，由于輻射換熱的背景溫度相關性，標定環境應該與使用環境具有接近的輻射換熱背景，或在傳感器表面安裝高反射比的風道以降低輻射換熱的影響。

根據試驗結果計算熱球風速探頭表面的Gr/Re2，繪制1400 Pa下的Gr/Re2曲線如圖7所示。當風速達到1 m/s以上時，無量綱數Gr/Re2恒＜0.01，即強制對流在總對流換熱中仍占據主導地位，在這個范圍內自然對流不會給測量帶來額外的誤差。

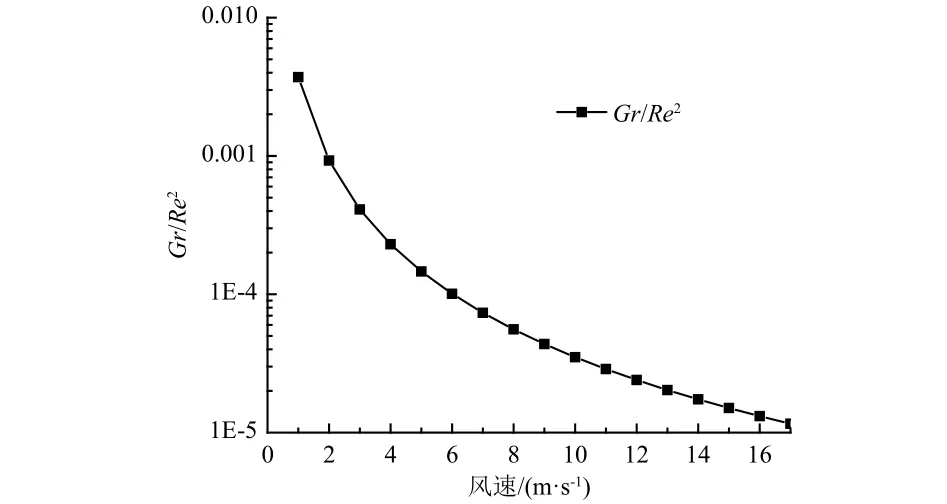
圖7 1400 Pa，不同風速下的Gr/Re2Fig. 7 Gr/Re2 at different wind speeds under the pressure of 1400 Pa

3 結論

針對低氣壓下的風速測量問題，本文使用無量綱數分析方法建立了恒熱流熱球風速探頭的風速?輸出信號模型，基于中型空間環境模擬試驗設備搭建了旋轉式低氣壓風速標定系統，分別在常壓、4×104Pa、1400 Pa的環境下進行了測試。得到了如下結論：

1）常壓下的試驗表明，本文建立的無量綱數分析模型與試驗測試取得了一致的結果，證明了該模型對于評估傳感器輸出的有效性。

2）4×104Pa下的試驗表明，無量綱數模型與試驗結果偏差主要集中在低風速范圍，在風速為2 m/s以上時，其偏差在10%以內，該模型可用于4×104Pa以上環境的熱球風速傳感器輸出信號預測。

3）1400 Pa下的試驗表明，無量綱數分析模型與試驗結果存在25%左右的偏差，對于極低氣壓下的熱球風速儀適用性分析，需要結合試驗手段進行修正；同時，0.6 mm探頭表面仍以強制對流換熱為主，探頭的靈敏度為0.1～0.2 mV/(m·s-1)，使用更高精度的采集儀器可以滿足1400 Pa下的風速測量需求。