巧用位置關系解決多元函數求范圍問題

浙江省寧波市鎮海區駱駝中學 (315202)

丁林蓬

例1 已知函數f(x)=x2+ax+b的兩個零點分別在區間(0,1)和(1，2)內，求3a+2b的范圍.

通常采用“線性規劃”的方式解決這一問題，過程如下：

解法1:依題意可得如下可行域，

筆者認為借助直線與曲線位置關系這一觀點，可以對這一問題進行這樣優化的解答：

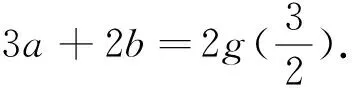
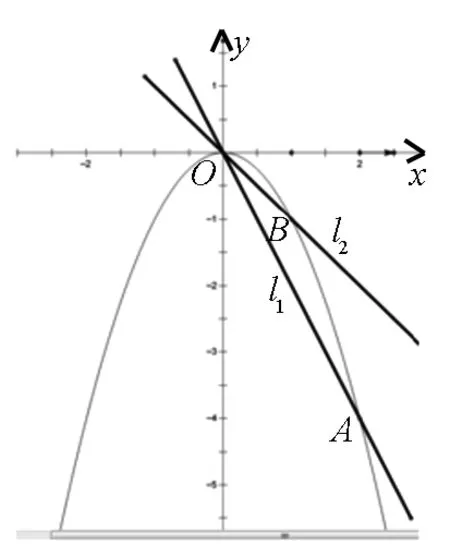
圖1

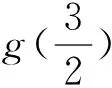
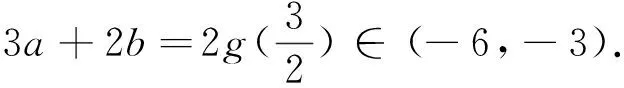
評析：解決數學問題的關鍵點是問題的轉化——面對新的問題，通過自己的思考將其轉化為某些已經解決過的數學問題.顯然，這兩種方法都是建立在轉化的基礎上展開的.

除此之外，筆者認為，解法2的“巧”體現在以下方面.

1.更加有效地避免“重復勞動”，更加方便快捷

例2 (2015浙江高考文科卷)設函數f(x)=x2+ax+b(其中a,b∈R).

(1)略；(2)已知函數f(x)在[-1,1]上存在零點，0≤b-2a≤1，求b的取值范圍.

參考文獻[1]中，利用“線性規劃”手段給出了兩種解法，現呈現一種如下：

解法1[1]：f(x)在[-1,1]上存在零點，即函數圖像與x軸有交點，分有一個或兩個交點進行討論：

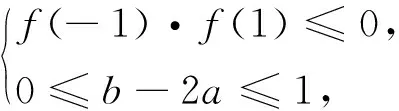
評析：正如原作者的點評，這一解法容易入手，想法比較自然，列出式子之后可以畫出可行域，但是對作圖的要求較高.

筆者認為，不僅如此，重復的繪制可行域，多次計算目標函數值，復雜的多項式都是繁瑣所在.由此，筆者給出法2如下，

解法2:這一問題可以變形為-x2=ax+b，直線與二次函數所表示的拋物線分別在區間[-1,1]內有交點(條件一).令g(x)=ax+b，根據0≤b-2a≤1，得0≤g(-2)≤1(條件二)，且有g(0)=b.由此，原問題轉換為：在條件一、二的前提下，計算g(0)的取值范圍.

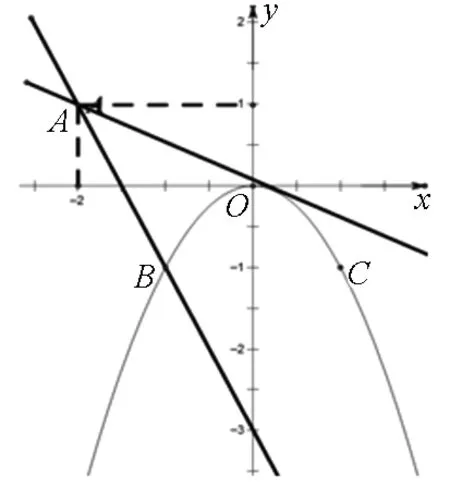
圖2

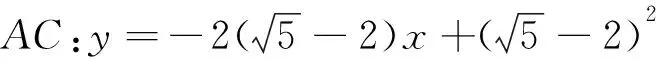
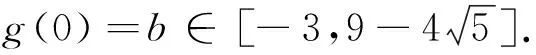
評析：這一過程更加注重思維，一定程度上使得重復、繁瑣的可行域繪制過程與目標函數的求解過程得到精簡，學生能夠更好地觸碰問題背后所蘊含的數學本質.

事實上，為了避免重復的計算過程，許多命題專家也會回避不必要的討論，如在這一問題的條件下，2017浙江省高考數學模擬卷(考試院測試卷)，將條件強化為“在區間(0,1)內有兩個零點”，解法這里不再贅述.

2.更加廣泛的使用范圍，更直觀的視覺呈現

波利亞在《怎樣解題》表中提出了“弄清問題、擬定計劃、實現計劃和問題解決”4個思維流程.關于計劃的擬定這一過程，解題方法適用的范圍越廣，越容易優先被選到.下面筆者談談解法2相對于解法1更廣泛的使用范圍.

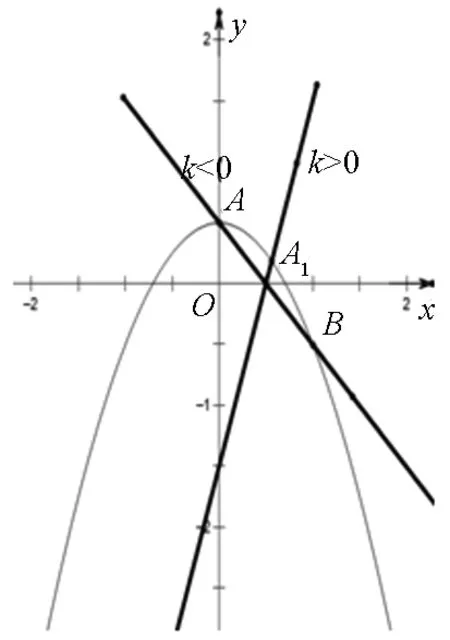
圖3

例3f(x)=2ax2+2bx(其中a,b∈R).若存在x0∈(0,t)對任意不為0的a,b均有f(x0)=a+b，則求t的取值范圍.

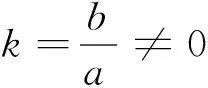
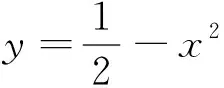
評析：顯然這里運用了直線與曲線位置關系這一視角，對原始一個復雜的數學問題進行了解答.“線性規劃”的手段是不能夠很好地解決這一問題的，因此，這一過程充分體現了優化之后方法的使用范圍之廣.下面筆者再舉一例.

例4 已知ex-x≥ax+b恒成立(其中a,b∈R)，試求a+b的最大值.

對這一問題，可令g(x)=ax+b，則原問題轉化為ex-x≥g(x)的條件下，計算g(1).可作圖4.

解法1:如圖4，由于ex-x≥g(x)，因此g(x)=ax+b的“臨界狀態”是g(x)為y=ex-x的切線.(x0,ex0-x0)為曲線上的點，由此可得該點處的切線方程為y=(ex0-1)x-x0ex0+ex0，也即g(x)=(ex0-1)x-x0ex0+ex0，x0∈R.由此得g(1)=-x0ex0+2ex0-1=h(x0)，由導函數可得g(1)≤h(1)=e-1.

解法2:如圖4，由于ex-x≥g(x)，因此g(x)=ax+b使得g(1)取最大值的“臨界狀態”，g(x)為y=ex-x在x=1處的切線.即g(1)=e-1.

評析：這一問題顯然與線性規劃問題相去甚遠，其原始考查內容是導函數與函數單調性之間的關系，難度較大.顯然，引入了直線與曲線的位置關系這一視角之后，原始的問題得到了直觀的呈現，得以更好地認識與解決.

在一個數學問題解決之后，作為在教學活動扮演者引導者角色的教師，可以在快節奏中停下來，悟一悟.優化一些已有的數學解題方法，透過問題表面探索數學本質，這樣才能更好地助力學生跨越一個又一個學習難關，不斷提升邏輯推理素養.