基于協差陣向量半范數的典型相關分析及其在量化投資中的應用
楊玉鋒,林偉城
(韶關學院 數學與統計學院,廣東 韶關512005)
隨著金融行業的高速發展,各類證券和期權類產品種類增多,交易量大增,很多模型已經不適合當今市場行情,隨之而來對量化投資[1-2]的研究變得越來越重要.量化投資是指借助現代統計學、數學的方法,從海量的歷史數據中尋找能夠帶來超額收益的多種“大概率”策略,并紀律嚴明地按照這些交易策略所構建的數量化模型來指導投資,以減少投資者情緒波動的影響,力求取得穩定的、可持續的、高于平均的超額回報.資金流向能夠幫助投資者透過指數(價格)漲跌預測到其他投資者的投資行為,并對此做出相應的應對策略.在金融交易系統中,一般能獲取收盤價、最高價、最低價、開盤價、持倉量、時間、成交金額以及成交量等數據,如果能通過統計分析找出這些數據之間的相關性,將對制訂有效的量化投資策略有著重要的指導意義.典型相關分析[3-4]是研究兩組變量之間相關關系的一種多元統計方法,能有效地揭示兩組變量之間的相互線性依賴關系.
在多元統計分析中,協差陣[3]扮演著重要的角色.筆者利用協差陣的對稱半正定性質,引入向量半范數[5]推導典型相關分析,并把結果應用到量化投資的回歸模型中.在后續討論中,用‖·‖2表示向量2范數.
1 基于向量半范數的典型相關分析
定義[5]設 p(x)是定義在 Rn上的一個非負函數,滿足:(i)p(αx)=|α|p(x),?x∈Rn,α∈R;(ii)p(x+y)≤p(x)+p(x),?x,y∈Rn,那么稱p(x)是Rn上的一個半范數.
定理 設A∈Rm×n是對稱半正定矩陣,那么定義了一個Rn上的半范數.
證 首先,當?x∈Rn,α∈R時,有:

由于A是對稱半正定矩陣,因此存在正交矩陣Q以及對角元非負的對角矩陣D,使得:

則當?x,y∈Rn時,有:
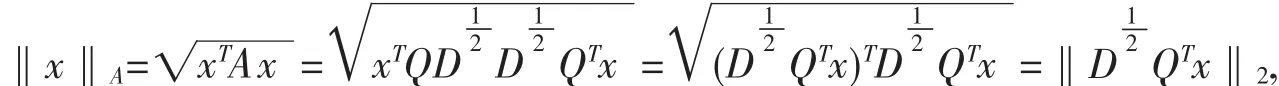
因此有:
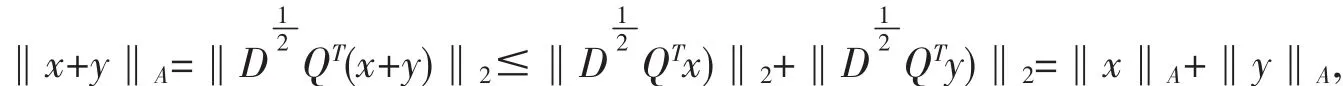
基于定理結果,可以利用該半范數給出隨機向量的典型相關分析理論.
設x,y是兩個n維隨機向量,a,b∈Rn,典型相關分析需要討論x,y線性組合aTx,bTy的相關性,即計算相關系數:


注1 (1)式定義的最優化問題形式比文獻[3]的形式更簡單,并且約束條件的意義更為直觀.
2 量化投資的回歸模型
量化投資問題中,能獲取收盤價、最高價、最低價、開盤價、持倉量、時間、成交金額以及成交量等交易數據,在對交易數據進行回歸分析[6]的過程中,關鍵在于選擇相關性較大的變量進行組合,進而結合典型相關分析完成回歸分析.接下來對(1)式的目標函數進行推導.
由 Cauchy不等式和譜分解定理[7],有:
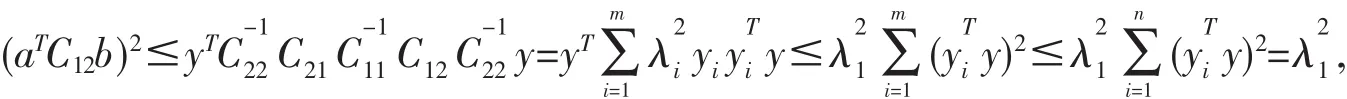
其中y∈Rn是矩陣的m個正特征值λ1≥λ2≥…≥λm>0對應的單位特征向量.另一方面,令:

其中a1,b1∈Rn分別由以下兩個線性方程組求解得到:

簡單計算可得:

這表明由(2)式給出的a1,b1可作為典型相關向量的線性組合系數.因此由約束最優化問題(1)可得到的第一對典型相關變量為:

注2 由于C11,C22是C的主子陣,因此均為半正定矩陣,從而(2)式中兩個線性方程組可采用MINRES方法[8]進行求解.另一方面,由于對稱性,計算主特征向量,可利用冪法結合Rayleigh商加速技巧進行[9].
根據上述討論,可以給出基于半范數典型相關分析的量化投資回歸模型:
①對收盤價、最高價、最低價、開盤價、持倉量、時間、成交金額以及成交量的數據進行規范化;
②按定義計算上述變量的樣本協差陣C;
④用MINRES方法求解(3)式中的兩個線性方程組得到a1,b1;
⑤按(4)式計算第一對典型相關變量u1,v1;
⑥按u1,v1的系數比例分配進行回歸分析,并做檢驗;
⑦對回歸分析結果進行背景解釋.
3 結語
本文利用樣本協差陣的對稱半正定性質,結合向量半范數理論建立了典型相關分析的約束最優化問題,并通過推導得到第一對典型相關變量,最后結合回歸分析給出了量化投資的數學模型.
半范數的引入得到了簡化的約束最優化問題,使得后續典型相關變量的推導更為直觀,類似的推導思路可以根據實際需求推廣到更深層次的典型相關變量的求解中.

