為數學點贊
——名師列析數學文化（8）數列

■北京市教育學院豐臺分院 張 琦

■北京市第十二中學高中部 高慧明

本刊特邀欄目專家簡介:

張 琦 北京教育學院豐臺分院數學教研員,骨干教師,中國教育學會輔導機構教師專業水平等級認證專家評委、命題專家。主編《高考復習三級跳》叢書數學卷,在全國知名學術期刊上發表有影響的論文數十篇。

高慧明 首屆全國十佳班主任,全國著名數學特級教師,國家教育部課程改革“全國先進工作者”,全國著名高考數學命題與考試研究專家,國家教育部“國培計劃”全國中小學教師培訓、班主任培訓、校長培訓特邀主講專家,受邀在全國各地做有關高考科學備考、班級管理等多場專題報告。現任教于北京市第十二中學高中部。

《普通高中數學課程標準（2017年版）》要求高中數學要將“數學文化融入課程內容”,并進一步指出:“在教學活動中,教師應有意識地結合相應的教學內容,將數學文化滲透在日常教學中,引導學生了解數學的發展歷程……”同時,課標特別指出“在教學中可以組織學生收集、閱讀數列方面的研究成果,特別是我國古代的優秀研究成果,如楊輝三角、《四元玉鑒》等”。

《數列》這一章的教材中,涉及了很多生活、生產中的數學問題。無論在東方還是在西方,古往今來,數列始終是數學研究的重要問題之一,歷史悠久,文化燦爛。

在古代中國,《莊子》中有“一尺之棰,日取其半,萬世不竭”的說法,而《易經》也有云“是故《易》有太極,是生兩儀;兩儀生四象,四象生八卦”,這里都包含了數列的含義。在西方,傳說古希臘畢達哥拉斯學派的數學家經常在沙灘上研究數學問題,他們在沙灘上畫點或用小石子來表示數,比如他們研究過1,3,6,10,…由于這些數都能夠表示成三角形,他們就將其稱為三角形數（如圖1）。類似地,1,4,9,16,…被稱為正方形數,因為這些數能夠表示成正方形（如圖2）。

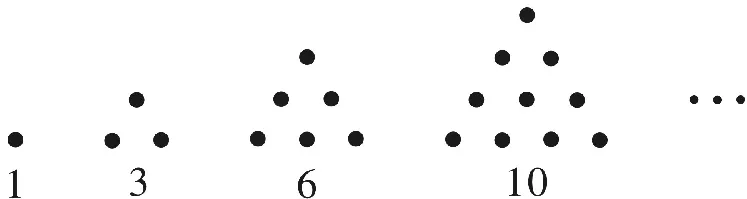
圖1

圖2

在人教版教材高中A版數學必修5第2章數列復習參考題A組中有這樣一道選擇題:

《萊因德紙草書》（Rhind Papyrus）是世界上最古老的數學著作之一。書中有一道這樣的題目:把100個面包分給5個人,使每人所得成等差數列,且使較大的三份之和的是較小的兩份之和,問最小的一份為（ ）。

這是一個“已知等差數列的項數n=5,前五項和S=100,以及a+a=（a+a51234+a5）,求a1”的問題。設公差為d,根據通項公式an=a1+（n-1）d以及前n項和公式得解。

本題中提到的萊因德紙草書是古埃及人用一種由紙莎草（Papyrus）壓制成的草片集制而成的,最初發現于埃及底比斯古都廢墟,1858年為蘇格蘭收藏家萊因德（H.Rhind）購得,因此得名。萊因德紙草書問題40即是:“五人按等差數列分100片面包,最少的兩份之和是另外三份的七分之一。問:五人各得多少?”紙草書中的解答采用了假設法進行解答,設最小的一項為1,則以后各項依次為1+d,1+2d,1+3d,1+4d。于是有2+為60,而已知各項之和為100,因此,各項乘會發現,數列的歷史悠久,有關數列話題古老,阿拉伯、古印度、中國古代、古希臘等的數學歷史中都有數列的主題,分布廣泛,人類對數列的認識很早,而且這些國家、地區對數列的認識也比較深入。下面我們就通過幾個簡單的例子進行闡述。

（一）古巴比倫人的數學智慧

考古學研究表明,古巴比倫人當時使用的是特殊的楔形文字,并把文字刻在泥板上曬干,曬干后的泥板變得和石頭一樣堅硬,可以長期保存;但歲月的侵蝕還是使得大部分泥板書消磨破損,保存下來的泥板書數量遠不及埃及的紙草書。不過,這并不影響后人對古巴比倫燦爛文化的全面了解。古巴比倫人對于數學的發現和記載,也是采用這種獨特的泥板書,在已經挖掘出的50萬塊古巴比倫泥板中,純數學泥板有300塊左右。

從這些存世發掘的數學泥板書中人們發現,古巴比倫人不僅早就形成“逢十進一”的概念,而且掌握了每隔六十進一的計數法。古代巴比倫人借助于圖3中的符號,可以表示所有的整數,如圖3所示。

圖3

在德國柏林博物館收藏的一塊古巴比倫數學泥板書上記載了這樣一道題目:兄弟10比倫的重量單位,其中1米那=60賽克爾）的銀子,相鄰的兄弟倆,比如老大和老二、老二和老三……所分銀子的差相等,而且已知老八分到的銀子是6賽克爾,求每人所得的銀子數量。通俗轉化的意思是:“10個兄弟分100兩銀子,一個比一個多,只知道每一級相差的數量都一樣,但究竟相差多少不知道,現在第八個兄弟分到6兩銀子,問每級間相差多少。”這是一則涉及等差數列的問題,古巴比倫人給出的解題方法是如此巧妙簡便,甚至連小學生也能理解。

他們的具體解答是:首先,要判斷出10個兄弟分得的銀子數,從老大到老十要么越來越多,要么越來越少。如果10個兄弟平均分這100兩銀子,則每人應該分到10兩。而現在第八個兄弟分到了6兩,說明只能是第二種情況,即老大分得多,往下是一個比一個少。其次,老大與老十的銀子數之和=老二與老九的銀子數之和=老三與老八的銀子數之和=老四與老七的銀子數之和=老五與老六的銀子數之和,這樣100兩銀子就分成了相等的5組,每組為20兩。最后,就從老三與老八的銀子數之和為20兩入手。由老八的銀子數6兩,可求出老三的銀子數為20-6=14（兩）,這就說明,老三比老八多得14-6=8（兩）。而老三與老八相差五級,因此可求得一級相差d=8÷5=1.6（兩）。

上述問題如果用現在的符號語言來描述的話,相當于已知等差數列的項數n=10,和Sn=100,a8=6,求公差。通過分析可以看出,古代巴比倫人已經總結出等差數列的性質:am+an=ap+aq（m,n,p,q∈N*,且m+

還有一個非常有意思的例子,地質學家W.K.勞夫特斯于1854年發掘出兩塊泥板（稱為森開萊泥板）其中一塊上面刻著一個數列,用現代符號來寫,前七個數是1,4,9,16,25,36,49。顯然這是一個自然數平方的數列。49以后自然應該是64,81,…。但記載的卻是1·4,1·21,…直到58·1。這一串數表示什么?猜測紛紛。事實上,這個問題只有在六十進位計數制中才能得到妥善的解釋:

1·4=1×60+4=64=8×8;

1·21=1×60+21=81=9×9;

……

58·1=58×60+1=3 481=59×59。

（二）古埃及人的數學

古埃及人主要用紙草作為書寫材料,紙草是尼羅河三角洲沼澤地盛產的一種水生植物,把這種草的莖依縱向剖成小薄片,然后壓平曬干使之成為紙卷,可用于書寫。由于埃及地區氣候干燥,因此有些紙草能幸運地保存至今。產生于公元前1700年左右的《莫斯科紙草書》和《萊因德紙草書》（RhindPapyrus）是現在我們研究古埃及數學的主要來源。

首先我們來看看《萊因德紙草書》中的一個例子:10人分10斗玉米,從第二人開始,各人所得依次比前一人少。紙草書上給出的解法是:“取10人所得的平均值,即1;從10中減去1,得9。取差數的一半,得,再乘以9,得加平均值1,然后依次從各份中減去差數,直到最后一份。”10份依次是:

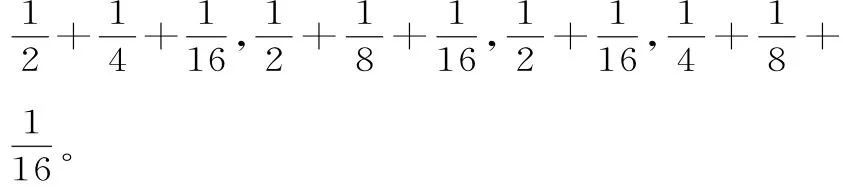
上述問題如果用現在的符號語言來描述的話,相當于已知等差數列的項數n=10,和法顯然具有一般性,用我們的記號表示,即人已經總結出等差數列求和公式:Sn=na1+

雖然紙草書中的問題絕大部分是實用性質的,但也有例外,例如《萊茵德紙草書》第79題:“7座房,49只貓,343只老鼠,2 401顆麥穗,1 6807赫卡特。”（如圖4）有人認為這是當時的一個數謎:7座房子,每座房里養7只貓,每只貓抓7只老鼠,每只老鼠吃7顆麥穗,每顆麥穗可產7赫卡特糧食,問房子、貓、老鼠、麥穗和糧食各數值總和。也有將房子、貓等解釋為紙草書作者賦予不同冪次的名稱,即房子表示一次冪,貓表示二次冪,老鼠表示三次冪,等等。無論如何,這是一個沒有任何實際意義的幾何級數求和問題,帶有虛構的數學游戲性質。

到中世紀,意大利斐波那契在1202年發表了《算盤全書》,書中有這樣一題:有七老婦人同往羅馬,每人有七騾,每騾負七袋,每袋盛有七個面包,每個面包有七小刀隨之,每小刀配有七鞘,問列舉之物全數共有幾何。顯然都是與上述問題類似的等比數列的求和問題。

圖4

（三）中國古代的數學

中國古代數學著作中有著豐富的數列知識,本文僅對其進行簡單的梳理。約成書于公元1世紀的我國古代最著名的數學典籍《九章算術》（如圖5）,它是中國古代第一部數學專著,其內容十分豐富,對戰國、秦、漢時期的數學成就進行了系統總結。

我們就對《九章算術》均輸章中的第17題、第19題進行簡單的分析總結。

均輸17:今有金棰,長五尺。斬本一尺,重四斤。斬末一尺,重二斤。問次一尺各重幾何。意思是:五尺長的金鞭,各尺重量依次成等差數列,靠根的一尺斬下來稱得重四斤,靠梢的一尺斬下來稱得重二斤。求中間三尺各重多少。

術曰（后面給的解題方法）:令末重減本重,馀即差率也。又置本重,以四間乘之,為下第一衰。副置,以差率減之,每尺各自為衰。副置下第一衰以為法,以本重四斤遍乘列衰,各自為實。實如法得一斤。翻譯成今天的數學符號語言就是:先求差率D=a5-a1,以“間數”4乘a5作為首項,然后從此項中依次減去D,得數列4a5,4a5-D,4a5-2D,4a5-3D,4a5-4D,再將所得數列各項同除以首項4a5,又同乘以a5,即得所求數列的各

圖5

這個例子告訴我們,《九章算術》中已經有了樸素的等差數列公差的求法:d=+（n-1）d。

均輸19:今有竹九節,下三節容四升,上四節容三升。問中間二節欲均容,各多少。意思是:有一根竹子,共9節,各節的容積依次成等差數列。已知較粗的下3節共容4升,較瘦的上4節共容3升。問各節的容積分別是多少。

術曰:以下三節分四升為下率,以上四節分三升為上率。上下率以少減多,馀為實。置四節、三節,各半之,以減九節,馀為法。實如法得一升,即衰相去也。下率一升少半升者,下第二節容也。簡單梳理解法就是:先求,之后可求得公差（“衰四升,所以易得下第二節的容積。

這個例子告訴我們,《九章算術》中已經有等差數列通項的性質:2an=an-1+an+1,以及數列的前n項和的一條性質:若等差數列前m項和為Sm,最后k項和為Sk,則:

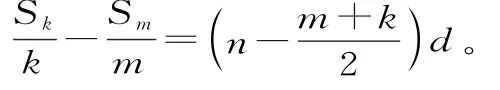
在中國古代,除《九章算術》以外,《孫子算經》（如圖6）也是一部重要的數學著作。其成書大約在四、五世紀,也就是大約1500年前,作者生平和編寫年不詳。傳本的《孫子算經》共三卷。這里面最著名的一道題目大概就是“雞兔同籠”問題了,今天我們不研究“雞兔同籠”問題,而是看另外一道題目:

圖6

“出門望九堤”:今有出門望見九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雛,雛有九毛,毛有九色。問各幾何。

這個問題是一個等比數列的問題,隱含著等比數列通項公式an=a1·qn-1的知識。

在課堂教學中我們一起去欣賞古今中外的數學史料和故事,感受數學的發展歷程,不僅可以增進我們學習數學的信心,而且可以使我們了解到不同文化背景下的數學思想,理解數學的多元文化。當數學沿著歷史的臺階走下神壇時,也揭開了數學文化神秘的面紗,真正向我們展示數學文化應有的人文價值。