使用Bootstrap方法計算認知診斷評估中的信度*

郭 磊，張金明

(1.西南大學心理學部，重慶 400715；2.西南大學統計學博士后科研流動站，重慶 400715； 3.中國基礎教育質量監測協同創新中心西南大學分中心，重慶 400715；4.重慶市腦科學協同創新中心，重慶 400715； 5.伊利諾伊大學香檳分校教育心理學系，香檳，伊利諾伊州 61820 美國)

1 引言

認知診斷評估(cognitive diagnostic assessment，CDA)已成為國內外測量學研究的關注熱點。CDA優勢為不僅能獲得被試能力水平，還能診斷其在知識點上的掌握情況。通過對知識狀態的估計，可知曉強項與弱項，指導教師開展針對性的教學補救，實現個性化教學。由此，認知診斷被視為新一代心理測量理論的核心(涂冬波，蔡艷，丁樹良，2012)。

CDA依賴測驗進行評估，因此，測驗質量決定了評估質量。測驗信度是衡量測驗質量的一個重要指標(溫忠麟，葉寶娟，2011)。一個良好的測驗，首先應該保證在評價同一批被試時，在不同時間或場合得到的測量結果是一致的。在心理與教育測驗中，常用信度來衡量測驗的穩定性，信度越高，穩定性越強。信度向來都是心理測量學的重要研究領域，國內外有關信度的研究數不勝數，但大多都屬于經典測驗理論或項目反應理論框架內的研究。而在CDA中，卻很少看見信度方面的研究。因此，對于同樣依賴測驗的CDA，對其信度的研究也就非常有必要和有價值。

目前，CDA中的信度研究剛剛處于發展階段，國內外相關研究主要有：(1)Templin等(2013)提出了屬性信度的計算方法，但未關注到模式信度的指標。本文將Templin的方法稱作“四分相關法”。(2)Cui，Gierl和Chang(2012)基于后驗概率分布信息，構建了分類一致性指標以衡量CDA中的模式信度，但未提出屬性信度。(3)Wang，Song，Chen，Meng和Ding(2015)基于前人研究，提出了屬性信度和模式信度指標，完善了之前的研究。和Cui等的方法進行比較后發現新指標具有同樣表現。本文將Wang的方法稱作“一致性法”。這些研究有一個相同的基本假設：被試在兩次相同測驗上估計的后驗概率分布和邊際分布分別相同。該假設的目的是為了構建重測信度(test-retest reliability)指標，但該假設與現實有些許不符。但凡測量總會存在誤差，即使同一批人第二次作答同一批試題，由于隨機誤差的存在，也很難保證前后兩次測驗的結果完全一致。在經典測驗理論中表現為觀察分數不一致，而在CDA中則表現為后驗概率分布、邊際分布不一致。因此，在CDA中開發出符合測驗實際情況，能夠將隨機誤差考慮在內的信度指標至關重要。本研究基于一次施測結果，采用Bootstrap方法對后驗概率及邊際分布抽樣，提出了兩類新的屬性和模式信度指標。第一類稱作積差相關法，有兩個指標：ARC(Attribute-level Reliability base on Correlation)和PRC(Pattern-level Reliability base on Correlation)；第二類稱作修正一致性法，有兩個指標：ARM(Attribute-level Reliability base on Multiplication)和PRM(Pattern-level Reliability base on Multiplication)。新指標同樣是通過計算兩次測驗結果的一致性來反映重測信度，不同之處在于構造第二次測驗結果的方式。四分相關法以及一致性法直接假設第二次測驗結果恒等于第一次測驗結果，而新方法將隨機誤差考慮在內，通過Bootstrap方法合理構造第二次測驗結果。為探查新指標在模擬和實證研究中的表現，本研究將與四分相關法和一致性法進行比較。

文章按如下方式組織：第二部分分別介紹四分相關法、一致性法、基于Bootstrap抽樣構建的新指標，并給出計算步驟。第三部分是模擬研究。第四部分是實證研究。最后一部分是結論與討論。

2 屬性和模式信度的計算方法

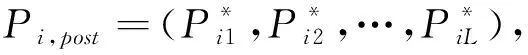
2.1 四分相關法

Templin等(2013)認為CDA中的屬性信度是前后兩次施測后被試在第k個屬性上掌握情況的一致性程度。由于知識狀態α是二分變量，故使用四分相關計算重測信度，其步驟為：

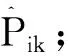
(1)

基于四格表計算四分相關，即得到屬性k的重測信度。

從公式(1)中可以看出，Templin等創建了第二次施測結果(實際并未施測)，并假設第二次估計結果恒等于第一次結果。經典測驗理論模型為X=T + E，X為觀測分數，T為真分數，E表示隨機誤差。該模型認為真實能力和觀察分數之間呈線性關系，并相差一個隨機誤差部分。盡管CDA測量模型與經典測驗理論不同，但基于同樣道理，即使是同一批被試作答同一份測驗，也很難保證兩次測驗的邊際概率完全一致。因此，四分相關法的前提假設較強，在現實中不太容易滿足，會得到誤差較大的信度估計值。

2.2 一致性方法

Wang等延續了Templin等對CDA中重測信度定義的思想，提出了屬性信度的計算方法：

(2)

和模式信度的計算方法：

(3)

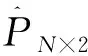
由公式(2)和(3)可以看出，這兩個指標的計算仍然假設第二次測驗的后驗概率分布和邊際概率恒等于第一次測驗的結果。該假設和Templin等一樣，偏于理想化。

2.3 基于Bootstrap的新方法

Bootstrap是以樣本來代表總體，在該樣本中進行放回抽樣，直至抽取n個數據組成一個樣本。這樣的程序反復進行多次，即可產生多個樣本，基于每個樣本數據就可以進行統計計算(江程銘，李紓，2015)。

2.3.1 屬性信度的計算

使用Bootstrap方法計算CDA的屬性信度步驟如下：

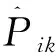
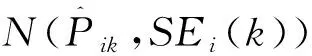
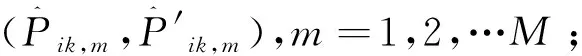
分別計算屬性信度ARC和ARM指標：

(4)

(5)

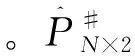
2.3.2 模式信度的計算

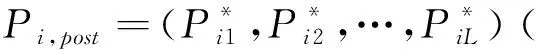
(6)

(7)

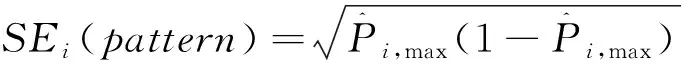
下面將分別通過模擬研究和實證研究比較四種方法在不同實驗條件下的表現。

3 模擬研究

3.1 研究設計

本研究以DINA模型(Culpepper，2015；de la Torre，2009；Junker & Sijtsma，2001)為例，但不局限于該模型。s和g參數均從U(0.15，0.25)中抽取。考察3個變量對信度估計的影響：(1)屬性個數K：3個和5個。(2)題目數量J：5題、10題、20題。Q矩陣如附錄表1和表2所示，行代表屬性數，列代表題目；1表示題目考察到該屬性，0表示未考察。K=3時，將Q10重復即可得20題的Q矩陣。(3)協方差矩陣Σ的非對角線元素ρ：0.2(低相關)、0.5(中相關)、0.8(高相關)。

1000名被試知識狀態的生成方式如下：依據多元正態分布MVNK(0，Σ)生成K維連續變量矩陣，設定各連續變量滿足標準正態分布，用0為切點對各連續變量進行兩段切割，并且可以通過設定Σ矩陣的非對角線元素ρ來調控各屬性之間的四分相關(詹沛達，陳平，邊玉芳，2016)。

Bootstrap取樣次數M設置為30000次。本研究為2×3×3的完全交叉設計，每個實驗條件重復30次，以減小隨機誤差。

3.2 信度真值的產生

固定被試的知識狀態、以及題目參數，使用DINA模型重復生成H次被試的作答數據，將這H次作答數據看作多次重測(test-retest)的結果。計算所有作答數據兩兩配對[H*(H-1)/2對]的估計一致性值，然后將這些一致性值的均值作為信度的真值rT，當重復數量足夠大時，均值可以逼近信度的真值，本研究中H取200次，該做法可參見Wang等(2015)的研究。其中，一致性值的計算方法采用Wang等(2015)文中的指標：

(8)

(9)

PTRCR1，2表示模式重測一致性指標，下角標1和2表示第一次和第二次施測。ATRCRk，1，2表示屬性k的重測一致性指標。

3.3 評價指標

①平均偏差

(10)

其中，rT為信度的真值，ri為每次實驗的信度估計值。該值越接近于0越好。

②誤差均方根：

(11)

3.4 研究結果

表1和表2是各個指標在不同實驗條件下屬性和模式信度估計結果的bias和RMSE值。圖1和圖2為對應的bias(A)和RMSE(B)折線圖。由于信度真值是H次作答估計一致性的均值，因此，bias和RMSE的本質是“離均差的和”與“離均差平方和的算術平方根”，兩者反映的是估計值與均值的波動大小。從整體上看，屬性信度的估計比模式信度穩定，偏差值更小。

就屬性信度來說，新方法對屬性信度的估計精確度更高。表現最好的是ARC方法，bias的絕對值離0最近，RMSE在大部分實驗條件下是最小的，從圖1中也可看出，其bias的趨勢線在0周圍波動最小，RMSE的趨勢線位于最下方。ARM的結果與一致性法表現基本相當，bias和RMSE與一致性法非常接近，ARM與一致性法的趨勢線基本重合。四分相關法表現最差，bias在0周圍波動最大，RMSE最大、趨勢線最高。屬性間相關性ρ對屬性信度的影響并未呈現一致性趨勢；隨屬性個數增加，估計偏差在整體上呈現不斷增大趨勢，bias波動變大，但ARC的表現仍最好；隨題目數量增多，估計偏差在整體上呈不斷減小趨勢。就模式信度來說，PRC、PRM的估計精度與一致性法相當，三種方法的bias和RMSE值非常接近。而在有些實驗條件下，PRC的精確性要比ARM和一致性法要高(表2的第2至第4行結果)。由圖2可知，PRC、PRM與一致性法的bias趨勢線波動幅度較一致，RMSE趨勢線也基本重合。除此之外，屬性間的相關性、屬性個數以及題目數量對模式信度的影響與屬性信度的結果基本一致。

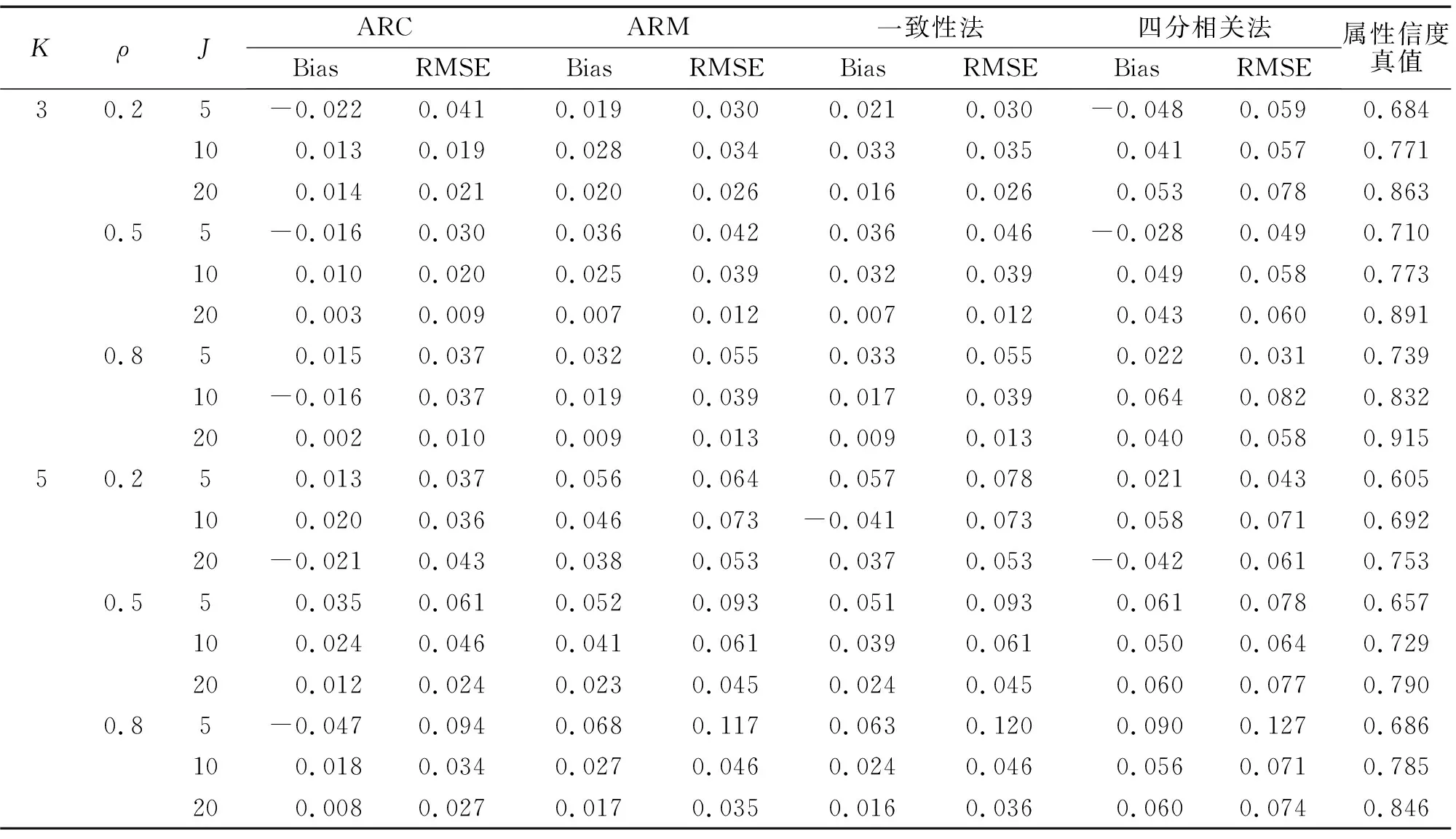
表1 不同方法的屬性信度估計精度結果

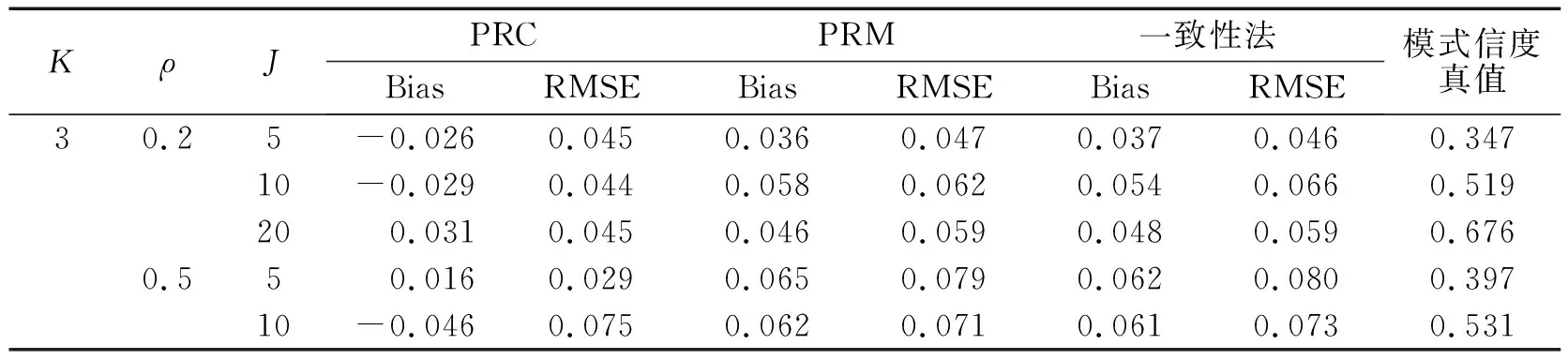
表2 不同方法的模式信度估計精度結果

續表2

KρJPRCPRM一致性法BiasRMSEBiasRMSEBiasRMSE模式信度真值200.0350.0620.0090.0150.0100.0150.7340.85-0.0270.0480.0650.0820.0670.0820.484100.0440.0730.0460.0590.0520.0610.644200.0180.0240.0140.0200.0170.0230.79550.250.0630.1170.0600.1070.0590.1070.23910-0.0660.1160.0640.1130.0640.1130.269200.0580.104-0.0470.0850.0510.0860.3480.55-0.1070.1580.1180.1560.1200.1560.285100.0690.1080.0630.0930.0610.0930.313200.0520.0940.0570.0870.0550.0860.4280.85-0.1070.164-0.1300.1770.1330.1810.334100.0430.0690.0380.0510.0390.0520.403200.0140.0210.0230.0370.0230.0380.574

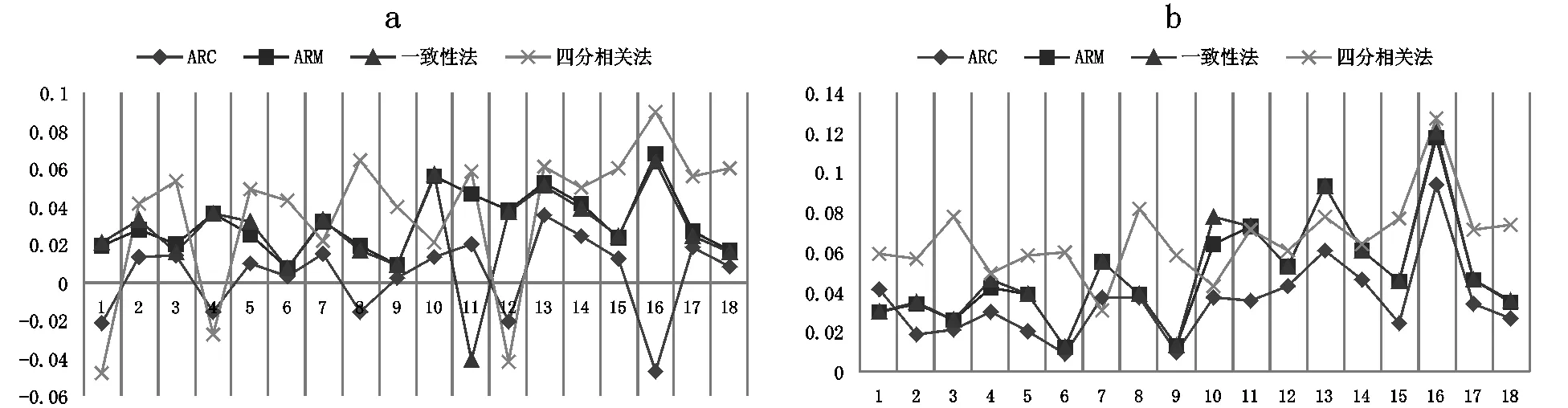
圖1 屬性信度的bias(A)和RMSE(B)折線圖

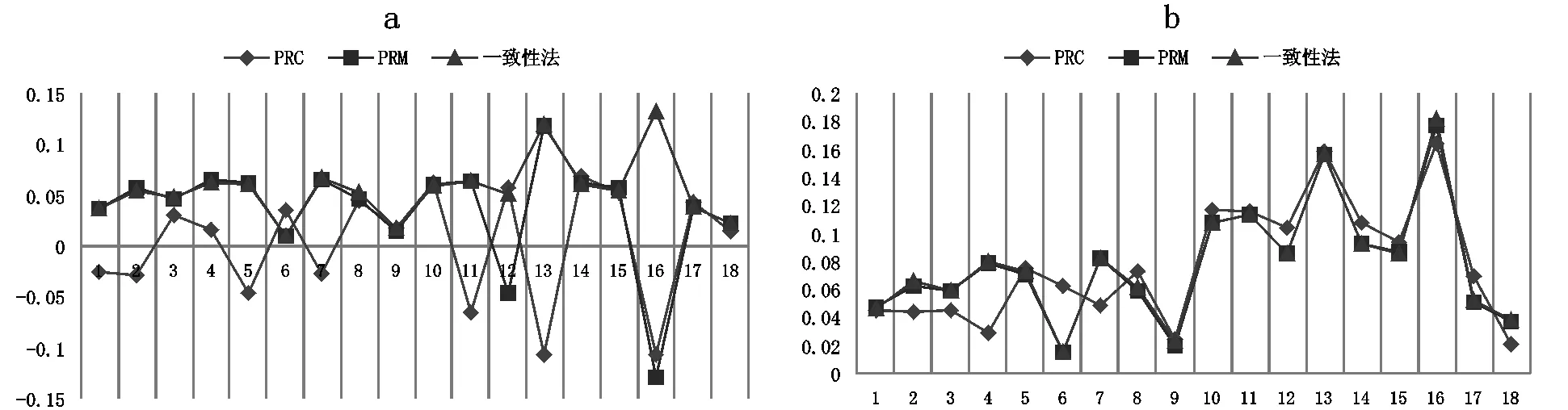
圖2 模式信度的bias(A)和RMSE(B)折線圖

4 實證研究

4.1 ECPE數據

該數據來自于R軟件CDM程序包中英語能力認證考試，包含2922人在28道題目上的作答數據，考察了3個屬性：構詞規則(Morphosyntactic rules)、銜接規則(Cohesive rules)、詞匯規則(Lexical rules)。作答矩陣和Q矩陣可分別由data.ecpe$data[，-1]和data.ecpe$q.matrix進行調用。

使用四種方法估計該數據的屬性和模式信度，結果見表3。

表3 ECPE信度估計結果

對于屬性信度，模擬研究結果表明，當屬性個數增大時，ARC的估計精確度最高，之后是ARM和一致性法，四分相關法表現較差。結合表3結果可知，使用四分相關法會高估ECPE的屬性信度(均值為0.888)，ARM和一致性法的屬性信度均值基本接近(0.86左右)，ARC估計的屬性信度均值為0.825。對于模式信度，模擬研究結果表明，PRC的表現較好，計算得到ECPE模式信度為0.616，而PRM和一致性法基本相當為0.685左右。有趣的發現是，不論使用何種指標，屬性A2的信度是最低的，通過表5的Q矩陣分析，A1考察了13次，A3考察了18次，而A2只考察了6次，說明考察次數會影響屬性信度。其原因可能有：①當屬性考察次數較少時，該屬性估計的準確性自然會降低，導致其穩定性降低；②影響信度的因素之一為測驗長度，在認知診斷中表現為屬性考察次數，當次數較少時，信度理應不會太高。

4.2 分數減法數據

分數減法數據同樣來自CDM程序包，包含536人在15道題上的作答數據，考察了5個屬性。作答矩陣和Q矩陣可分別由data.fraction1$data和data.fraction1$q.matrix進行調用。使用四種方法估計該批數據的屬性和模式信度，結果見表4。

模擬研究表明ARC表現最好，表現最差為四分相關法。結合表4結果可知，四分相關法仍高估屬性信度(均值為0.876)，ARM和一致性法估計的屬性信度均值接近(均值為0.86左右)，ARC估計的屬性信度均值為0.818。對于模式信度，模擬研究結果表明當屬性個數增加后，PRC、PRM和一致性法基本相當，模式信度約為0.6左右。同樣，屬性A5的信度最低，其次是A2和A4。這是因為A5只考察了3次，A2和A4分別考察了8次和9次，A1和A3分別考察了14次和12次。

5 結論與討論

信度是衡量測驗質量的一個重要指標，CDA同樣需要重視信度問題。本文基于Bootstrap抽樣思想，提出了兩類計算屬性和模式信度指標。新指標更加符合現實，突破了“假設被試兩次測驗的后驗概率和邊際概率完全相同”的局限。通過模擬和實證研究，與四分相關法和一致性法進行比較，驗證了新指標的優越性，得到了以下主要的結論：

(1)整體上，屬性信度的估計比模式信度穩定，且偏差更小；

(2)對屬性信度而言，ARC表現最優，其次是ARM和一致性法，四分相關法表現最差。屬性個數增加會增大估計偏差，題目數量增加則會減小其估計偏差；

(3)對模式信度而言，PRC、PRM估計精度與一致性法相當。屬性間相關性、屬性個數、題目數量對模式信度的影響與屬性信度基本一致；

(4)實證研究可知，每種方法均能報告屬性和模式信度。結合模擬研究結果，積差相關包括的兩個指標(ARC和PRC)表現較好。想要提高屬性信度，可適當增加該屬性考察次數。

綜上所述，計算屬性信度時，綜合排名為：ARC>ARM≈一致性法>四分相關法，推薦使用ARC。計算模式信度時，綜合排名為：PRC>PRM≈一致性法，推薦使用PRC。

本文結合模擬和實證研究結果，擬探討以下幾個問題：

5.1 ARC與PRC相關說明

5.2 不同參數估計方法對信度的影響

Huebner和Wang(2011)比較了三種參數估計方法：后驗眾數法MAP、后驗期望法EAP、極大似然估計MLE。不同的估計方法影響后驗概率分布和屬性邊際概率，進而影響標準誤，導致Bootstrap抽樣范圍發生變化。本文基于MAP得到的結果計算的信度，未來需探討不同參數估計方法對信度的影響。

5.3 不同認知診斷信度指標的開發

在經典測驗理論中，除重測信度，還有復本信度、內部一致性信度等。不同信度指標，其關注點不同，應用場景也不同。在報告信度時，需指出是何種信度。目前關于CDA中信度的研究，均從重測角度出發，這是因為該方法易于理解、指標容易構建。未來應考慮如何將其余信度指標拓展至CDA中，豐富CDA的信度指標體系。

除上述問題之外，不同的屬性層級結構可能會對信度的估計帶來影響，未來研究可以嘗試在不同的屬性層級結構下，以及不同認知診斷模型下探討本文所提出新指標的表現。