偏置鋸切力對圓鋸片輻射噪聲能量影響的研究

李金良，馬嘯民，崔鑫偉，呂士海

(燕山大學 機械工程學院，河北 秦皇島 066004)

0 前言

大型圓盤金屬鋸切設備廣泛應用在型鋼熱軋車間里，用于鋸切各種高溫狀態(750 ℃～1 000 ℃)下的異形斷面軋件和擠壓件。其具有斷面平整、切口處精度高、切割速度快、生產效率高、使用成本低等優點。但是熱鋸機在鋸切過程中產生的噪音污染極為嚴重，最大噪音等級可達到120 dB，極大的危害設備操作者的身體健康。

圓盤鋸鋸切過程中，鋸齒與工件之間的斷續接觸產生的沖擊使鋸片產生強烈的局部振動。現定義鋸片為其表面各點在平衡位置附近的軸向往復運動。引起鋸片振動的主要因素是鋸齒沖擊力與動不平衡力。由于鋸片直徑和厚度之比很大，軸向剛度低，易造成鋸片的軸向振動，而鋸片的軸向振動引起的空氣振動是鋸切噪聲的根本原因。本文以鋸切力在此振動下造成的軸向偏置作為研究前提，利用有限元法來研究鋸片的固有屬性以及其在偏置鋸切力激勵下的強迫振動響應。

1 鋸片振速均方值的有限元表達式

由文獻[1,2]可知，鋸片表面輻射噪聲與鋸片表面振動速度有著密切關系，并且鋸片表面輻射噪聲量可以按板的噪聲輻射情況進行考慮。因此，鋸片輻射的噪聲輻射能量為：

(1)

式(1)為結構振動與介質相互作用下，空間輻射聲能量最一般的表達式。結構聲輻射效率δrad是反應介質與聲輻射機構相互作用的一個物理量，它與結構的形狀、幾何尺寸、邊界條件及激勵形式有關。

(2)

式(2)的有限元表達式為：

(3)

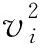
2 鋸切力作用位置偏置原因

鋸片在鋸切過程中，由于同時受到徑向、切向兩個方向的激振力，從而導致鋸片的強迫振動。這兩個方向的力是由于鋸切過程中鋸片的鋸齒與工件相互撞擊產生的，屬于高頻率的周期脈沖激勵[3]。在理想的鋸切狀態下，徑向力和切向力都均勻的分布在鋸齒上且都垂直于鋸片的軸心。而在實際的鋸切中，由于鋸片的所處工況非常復雜，例如鋸片鋸齒的形狀制造誤差以及制造、安裝過程中產生的動不平衡會引起鋸齒的軸向振動，從而產生偏斜。由于這種情況的存在，導致了鋸齒在與工件接觸時會由于鋸齒的軸向位移而導致徑向力和切向力相對鋸片中心平面產生軸向偏移量L，嚴重影響著鋸片的聲輻射能量，如圖1所示。

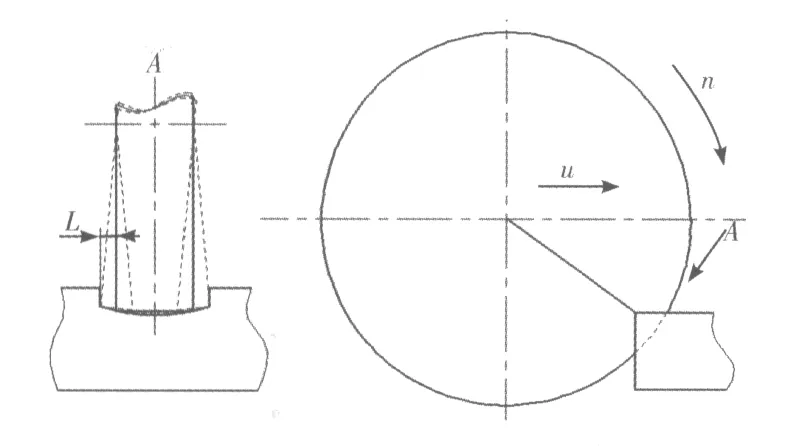
圖1 鋸片工況軸向偏移示意圖

3 單元類型的選取及材料屬性設置

本文采用有限元(FEM)方法研究鋸片的徑向力和切向力的作用位置對鋸片工作中產生的加速度噪聲的影響。為了兼顧FEM的計算效率和分析結果的精度，將在保留圓鋸片主要結構特征和力學特性的基礎上，對實際物理模型按照一定原則進行簡化。根據以往研究[4,5]，在研究鋸片振動時，可忽略鋸齒形狀的影響從而將其簡化為一圓盤。

鋸片在鋸切工況下，基體承受彎曲載荷的同時也承受扭曲載荷，基于受力特性，選擇體單元solid45定義結構，φ2 000鋸片鋸片直徑D=2 000 mm，夾盤直徑d=900 mm，鋸片厚度δ=10 mm，鋸片基體材料為65Mn，彈性模量E=2.06×1011N/m2，泊松比μ=0.3，密度ρ=7 850 kg/m3，65Mn材料阻尼系數1‰[6]。

4 網格劃分及邊界條約束件的施加

因為φ2 000 mm鋸片的厚度遠遠小于鋸片直徑，所以對鋸片的厚度方向(軸向)劃分4個單元，直徑方向(徑向)劃分27個單元，總計17 280個單元，22 400個節點，有限元模型如圖2所示。φ2 000 mm鋸片的夾盤直徑為φ900 mm，由于夾盤通過螺栓緊緊的壓在鋸片表面從而使鋸片固定在轉軸上。同時，因為夾盤厚度遠大于鋸片厚度使夾盤的軸向剛度遠大于鋸片，因此可認為夾盤位置的鋸片表層軸向、徑向、切向位移受到了約束。對鋸片表面層位于夾盤直徑內的節點分別在x、y、z三個方向上施加位移為0的約束。

圖2 鋸片有限元模型

5 徑向和切向脈沖力作用位置的分析與施加

由于鋸片厚度相對于鋸片直徑非常小，所以在鋸片厚度方向劃分了5個節點，如圖3所示。

圖3 軸向節點編號

由于位置點1、2和5、4關于鋸片對稱平面上的位置點3對稱，所以當徑向和切向脈沖力分別作用在位置點1和5時，引起的鋸片軸向振動響應關于鋸片對稱平面對稱，即所有對稱節點上的振動幅值相等且相位相反。因此在研究徑、切向脈沖力作用位置偏移而引起鋸片軸向振動特性的變化時，可近似取脈沖力分別作用在位置點1、2、3上時的軸向振動特性進行對比分析。根據文獻[7]可知，φ2 000 mm的鋸片在鋸切的工況下振動能量主要分布在2 000 Hz以下，徑向力與切向力的比值約為5～18，本文取12。所以在鋸片的1、2、3位置點分別施加切向力Pt=50 N和徑向力Pr=600 N時，對鋸片進行1 000～2 000 Hz諧響應分析。

用ANSYS進行諧響應分析時，在某一個頻率點處，鋸片的實際振型是由許多振動模態疊加而成的，根據模態貢獻因子可以確定在某一個頻率點起主導作用的振動模態，以下分析如不加特殊說明，振型均為起主導作用的模態振型。由于鋸片具有軸對稱性，可以近似的簡化成一個圓盤。根據文獻[8]，其振動模態的空間解分為三種模態振型：(1)軸向振動模態可用節圓數m和節徑數n來表達，其表示方法為a(m，n)；(2)徑向模態可用節徑數n來表達，其表示方法為(r，n)；(3)周向模態也可用節徑數n來表達，其表示方法為(l，n)。

6 徑向脈沖力偏置數據分析

圖4為徑向力Pr=600 N分別作用在位置點1、2、3上時其軸向振速均方值在1 000～20 00 Hz的頻響曲線。當徑向力作用在點3時，在頻率1 788 Hz處，振速均方值有最大值6.35E-09，振型為(r，2)。其次是在1 184 Hz處，振速均方值為3.53E-09，振型為(l，1)。徑向力作用在2點時，在頻率1 243 Hz，振速均方值有最大值2.32E-2，振型為a(3，7)。其次是在1 205 Hz處，振速均方值為1.17E-2，振型為a(0，19)。徑向力作用在1點時，在頻率1 243 Hz，振速均方值有最大值9.31E-2，振型為a(3，7)。其次是在1 205 Hz處，振速均方值為4.60E-2，振型為a(0，19)。可以看出，徑向力作用在1點和3點時最大振速均方值的相差7個量級，而作用在1點和2點時最大振速均方值處于一個量級且相差較小。

圖4 徑向力1 000～2 000 Hz振速均方值頻響曲線

圖5為徑向力作用時1 000～1 300 Hz軸向振速均方值頻響曲線。當徑向力作用在1點時，振速均方值峰值密集且其對應的模態大部分為軸向模態，振速均方值峰值也特別的大，所以想要使激勵頻率避開共振頻率減振是不可行的。由于徑向力作用在3點時，其對應峰值的模態數量遠小于節點1和2的峰值模態數量，且其峰值對應的模態振型在1 000～2 000 Hz范圍內既有徑向模態(r，2)，也有周向模態(l，1)，但是徑向模態(r，2)的峰值大于周向模態(l，1)的峰值，說明鋸片在純徑向力激勵的條件下，在激勵起徑向模態的同時也會激勵起一部分周向模態，但是徑向模態在振動過程中占主導地位。無論是徑向模態還是周向模態，其振型對應的鋸片兩面上各個節點的軸向位移都是關于節點3對稱且幅值相同，相位相反。在相同的振動能量下，限制了節點的軸向位移從而使振速減小。

無論是在振速均方值數量級大小上還是在主導模態個數上，軸向模態都大于徑向模態和周向模態。軸向模態比徑向模態更能引起鋸片與空氣之間有效的能量交換。所以在聲輻射功率上軸向模態的貢獻率遠大于徑向模態的貢獻率，鋸片噪聲輻射功率主要是由其被激勵起的軸向模態決定的。同時也可以推出，在考慮鋸齒上徑向力軸向偏移的作用時，徑向力的作用位置對鋸片的聲輻射功率影響明顯。在徑向力作用于位置點3處時，鋸片的振速均方值較小。當鋸片徑向力作用位置出現軸向偏移并且偏移距離增加時，其所激勵起鋸片的振速均方值有明顯的增加，且最大量級增加7個量級。

圖5 徑向力1000～1300Hz振速均方值頻響曲線

7 切向脈沖力偏置數據分析

圖6為切向力Pt=50 N分別作用在位置點1、2、3上時其軸向振速均方值1 000～2 000 Hz的頻響曲線。

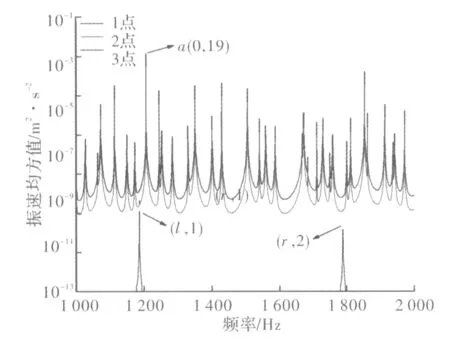
圖6 切向力1 000～2 000 Hz振速均方值頻響曲線

切向力作用在3點時，在頻率1 184 Hz時，振速均方值有最大值3.73E-10，振型為(l，1)。其次是在1 788 Hz處，振速均方值為5.71E-11，振型為(r，2)。切向力作用在2點時，在頻率1 205 Hz處，振速均方值有最大值6.45E-4，振型為a(0，19)。其次是在1 852 Hz處，振速均方值為1.09E-4，振型為a(0，23)。切向力作用在1點時，在頻率1 205 Hz處，振速均方值有最大值2.62E-3，振型為a(0，19)。其次是在1 852 Hz處，振速均方值為4.43E-4，振型為a(0，23)。其部分振型圖如圖7所示。切向力作用在1和3點時最大振速均方值平均相差6個量級，而作用在1點和2點時的振速均方值都處于同一個量級切相差較小。

圖7 各階主導模態振型圖

圖8為切向力作用時1 000 ～1 300 Hz振速均方值。從圖8中可以看出，切向力作用在1點時，振速均方值峰值密集且其對應的模態大部分為軸向模態。由于切向力作用在3點時，其對應峰值的模態數量遠小于節點1和2的峰值模態數量，且其峰值對應的模態振型在1 000～2 000 Hz范圍內既有徑向模態(r，2)，也有周向模態(l，1)，但是周向模態(l，1)的峰值大于徑向模態(r，2)的峰值，這說明鋸片在純切向力激勵的條件下，在激勵起周向模態的同時也會激勵起一部分徑向模態，但是周向模態在振動過程中占主導地位。可以看出，在考慮鋸齒上切向力軸向偏移的作用時，切向力的作用位置對鋸片的聲輻射功率影響明顯。在切向力作用于鋸齒的中心點3處時，鋸片的振速均方值較小。當鋸片切向力作用位置出現軸向偏移并且偏移距離增加時，其所激勵起鋸片的振速均方值有明顯的增加，且最大量級增加6個量級。

圖8 切向力1000～1300Hz振速均方值頻響曲線

8 結束語

鋸片在偏置的徑向力或切向力作用下，都會激振起鋸片的軸向振動模態從而使噪聲輻射量明顯增加。由于徑向力和切向力分別作用在1點時的速度均方值平均值相差三個量級。所以在考慮鋸齒上偏置徑向力與切向力同時作用時，切向力對振速均方值的影響遠小于徑向力對振速均方值的影響，可以忽略不計。所以，在計算鋸片聲輻射功率時時，應主要考慮徑向力軸向偏置影響。