新型鋼管打捆機械手的結構設計及仿真分析

李 震，柴曉艷

(1.天津理工大學 天津市先進機電系統設計與智能控制重點研究實驗室，天津 300384；2.機電工程國家級實驗教學示范中心(天津理工大學)，天津 300384)

0 前言

隨著我國工業的產業結構逐漸升級，國內的鋼材用量增長迅速，特別是鋼管行業取得了長足發展，我國的鋼管產量多年來穩居世界首位，國內相關行業對于鋼管生產設備的性能提出了更高的要求。傳統的鋼管打包機設備體積大，且無法對廢舊鋼帶進行利用，新型鋼管包打捆機械手將鋼管包打捆動作與機器人技術有機的結合起來，使用廢鋼帶對鋼管包進行打捆，不僅提高了打捆機械手的工作效率，且降低了生產成本[1]。

1 新型打捆機械手的整體設計分析

新型打捆機械手機械結構的設計關系到后續的仿真分析和優化設計，特別是對關鍵部件的設計對機械手的有限元輕量化和美觀性有著重要影響。對機械手進行完整的結構設計后，需要根據設計的尺寸和裝配方式對機械手進行三維建模，應用三維設計軟件soildworks對機械手進行三維模型設計。

1.1 現有鋼管打捆設備

我國鋼帶打捆設備的研制起步較晚，但經過近30年的發展，已研制出暫時適合國內使用的打捆設備。如圖1、圖2所示為國內目前使用較為廣泛的兩款打捆設備。

圖1為采用標準鋼帶包打捆的打捆設備，這款設備穩定性好，而且標準成捆的鋼帶厚度較小、較易彎折，打捆過程中將標準成捆的鋼帶包首先放置在打捆設備上，然后再使用該設備進行拉緊動作。圖2為目前國內使用較多的簡易打捆設備，這款設備可以使用廢舊鋼帶進行打捆，采用人工打包方式在鋼管槽中進行打包，降低了生產成本，但是在打捆過程中的打捆動作需要很大部分的人工參與，自動化程度較低。

圖1 采用標準鋼帶的鋼管打捆機

圖2 廢帶打捆簡易設備

針對以上兩種使用較多的打捆設備，存在明顯缺陷，圖1中設備采用標準鋼帶進行打捆，成本較高；圖2中設備雖然使用了廢鋼帶，但設備自動化水平較低，又不利于生產效率的提高。針對目前國內存在的情況，本文設計的鋼帶打捆機械手從實際生產出發，將廢舊鋼管進行重新利用，裁剪成標準長度鋼帶，在打捆過程中使用廢鋼帶進行打捆，并利用機器人技術完成打捆動作，具備了較高的自動化程度。

1.2 新型打捆機械手的結構設計與分析

在實際生產中，六角形鋼管包相比于其他形狀的鋼管包型，鋼管之間更加緊密、運輸過程更加平穩，新型的鋼管包打捆機械手主要針對六角形鋼管包進行打捆。在對打捆機械手進行設計之前需要對鋼管包的尺寸進行分析計算，鋼管包的周長和高度會對鋼帶長度和機械手的運動產生影響，由于在對鋼管包完成打捆后，所有鋼帶應有30～70 mm的重疊部分來完成后續的焊接工作，本文主要針對常用外徑21.3～114 mm系列共9種型號的鋼管包進行分析，各型號鋼管包的主要參數經計算后如表1所示。

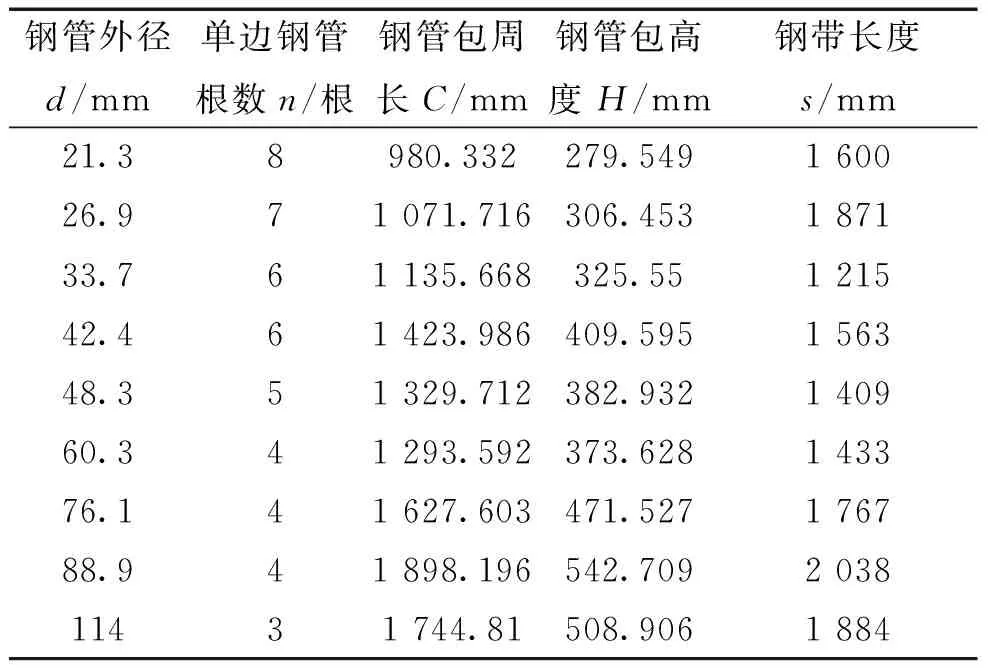
表1 六角鋼管包主要參數

針對鋼管包打捆任務的工作要求，新型打捆機械手需要具備以下兩個功能：對廢鋼帶的抓取動作、帶動鋼帶跟隨機械臂對鋼管包進行打捆夾緊，與傳統的鋼管包打捆設備不同，新型打捆機械手實現了對廢鋼帶的重新利用。

新型打捆機械手機械臂和末端抓取機構的結構簡圖如圖3、圖4所示，其中L1、L2、L3分別為機械手的基桿、中間桿和末端執行桿，各桿件之間由轉動關節連接，由伺服電機(圖中未畫出)進行轉動角度的控制，實線L1、L2、L3表示機械臂運動的初始位置，粗點畫線L1′、L2′、L3′表示機械臂運動的末位置；鋼帶右端的A點為末端抓取機構對鋼帶的抓取點，x0、y0分別為基座的橫坐標、縱坐標，H為鋼管包的高度，C為表1中鋼管包的周長，S1、H1分別為基座在X、Y方向的結構所需長度，根據伺服電機尺寸大小，本文分別取220 mm、195 mm，S2為末位置時末端抓取機構的抓取點與中心線的距離，這個距離既需要保證打捆機械手在運行即將結束時不發生碰撞，也要給后續的焊接工作留有足夠的操作空間，這里取40 mm作為工作空間。

末端抓取機構是新型打捆機械手對鋼帶進行打捆動作時的關鍵部位，末端抓取機構主要是要完成對鋼帶的夾緊動作。夾緊機構為左右對稱結構，選擇氣缸驅動的方式。當氣缸活塞桿下移時，帶動連接件1向下運動，在連桿4(5)和副桿2(3)的共同作用下，推動連桿6(7)繞鉸鏈E(F)旋轉,推力進入夾緊鉗8(9)；隨后夾緊鉗8(9)繞著固定鉸鏈C(D)進行回轉運動。當連接件1下移到一定的位置時，在整個增力機構的作用下，完成對鋼帶AB的夾緊動作。

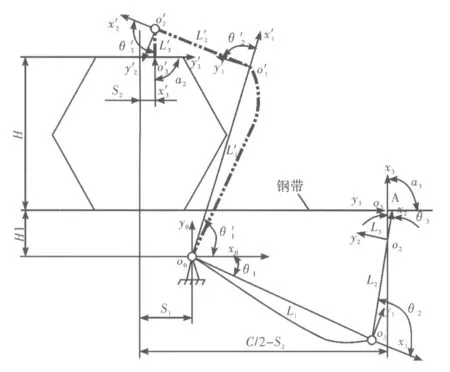
圖3 新型鋼帶打捆機械手機械臂結構簡圖

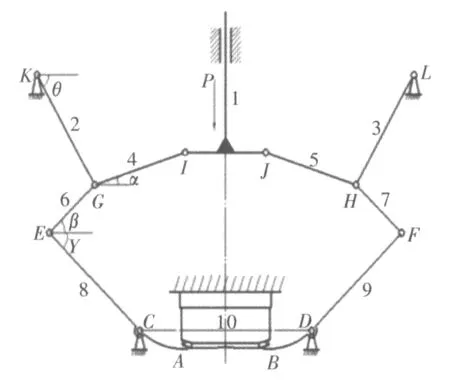
圖4 壓緊狀態下末端抓取機構簡圖

在初始位置時根據不同鋼管包型的鋼帶長度，調節三機械臂的位置使得兩側末端抓取機構恰好處于鋼帶的首末兩端(即圖3中A點)。打捆機械臂和末端抓取機構的整個運動過程分為“夾緊”、“打捆”、“復位”三個行程。首先，兩端抓取機構在氣缸的作用下，通過自身增力機構獲得夾緊鋼帶所需的夾緊力，將鋼帶牢牢夾緊，保證在運動過程中鋼帶不會脫離機械手；隨后，三個機械臂在各自關節伺服電機的作用下，各自完成需要轉過的角度，到達機構運動的末位置，使得鋼帶兩端重疊在一起，進而進行焊接作業，完成“打捆”動作。最后，在完成對鋼帶的焊接工作后，氣缸活塞桿收縮，帶動末端抓取機構松開鋼帶，機械手完成“復位”。至此，打捆機械手進行了三個工作行程，完成了對鋼管包的打捆[2]。

在打捆機械手機構設計中，由于最大包型與最小包型之間的鋼帶長度與鋼管包高度之間的差距較大，所以為安全起見按照最大包型設計的設備尺寸在打捆較小包型時，會顯得桿件過長，整體尺寸過大，不利于現場工作空間的合理利用，因此針對這9種包型設計出兩套打捆機械手來完成作業任務，兩套設備的主要結構尺寸參數見表2，打捆完成后效果圖如圖5所示。在soildworks中按照各桿件的尺寸以及相對位置完成裝配，如圖6所示為打捆機械手的示意圖[3-6]。

表2 兩種型號的打捆機械手各桿件的長度

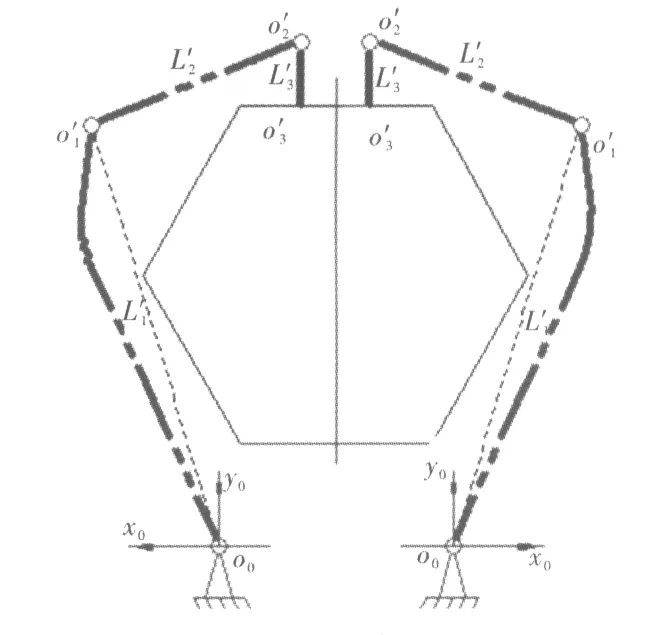
圖5 打捆完成示意圖

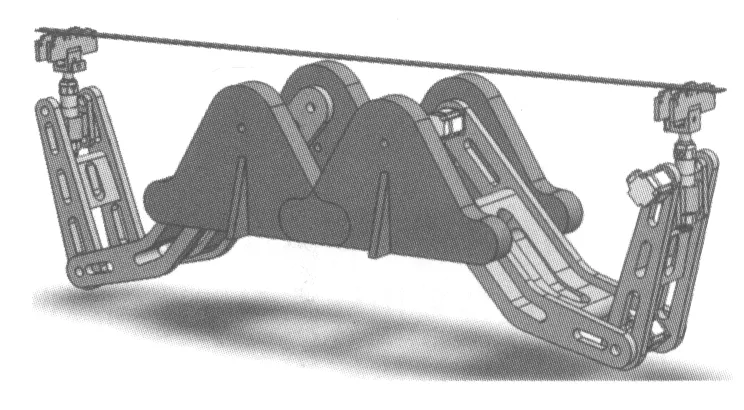
圖6 新型打捆機械手示意圖

2 基于ADAMS的新型打捆機械手建模及仿真分析

ADAMS是目前國內使用較為廣泛的虛擬樣機技術軟件，可以對實體模型進行仿真運行、結構優化、數據處理等操作，但ADAMS也存在著建模功能差等缺點，所以本文采用soildworks與ADAMS聯合建模的方法對打捆機械手進行建模，并使用ADAMS中自帶的離散型柔性體建模方法對打捆用鋼帶進行建模，最后在ADAMS中進行仿真分析[7]。

對打捆機械手進行仿真分析，首先可以驗證根據運動學方程編制的驅動函數是否合理，即各關節能否協調整個機械手完成打捆動作。其次，由仿真后得出的速度和加速度圖像可以預測出實際運行時的振動情況，為驅動函數的改進提供數據參考。最后，由仿真得出的各關節力矩值，可以為后續對初步設計后的關節電機和減速器進行重新選型提供數據支持，進一步改進設備結構。

2.1 新型打捆機械手模型的建立

Adams中的模型在仿真過程中有時需要發生變形才能完成任務動作，構件的變形需要建立柔性體構件來完成。ADAMS中有兩種柔性體建模方法：一是離散型柔性體建模法，這種方法是將一段剛性構件分割成有數段的剛體，小剛體中間用柔性力來連接，由此來模擬柔性體的變形，適用于大變形的簡單構件；二是使用ADAMS/Flex建立柔性體，適用于較復雜的構件。由于打捆機械手使用的鋼帶需要發生較大變形才能將鋼管包捆住，且鋼帶外形簡單，因此在建立廢鋼帶柔性體模型時選擇離散型柔性體建模法進行建模[8]。

對于φ21.3～φ114 mm系列共9種型號的鋼管，考慮到新型打捆機械手可以完成對最大周長的鋼管包進行打捆時，就可以完成所有型號鋼管包的打捆，兩套設備需打捆的最大包型分別為φ88.9 mm和φ42.4 mm型鋼管包，考慮到φ42.4 mm型鋼管包與φ88.9 mm型鋼管包建模及仿真方式完全相同，因此本文只對φ88.9 mm型鋼管包進行建模，φ42.4 mm型鋼管包的仿真只給出仿真結果。在對打捆機械手進行建模之前，首先應完成鋼管包模型的建立。

在打捆機械手仿真運行時由于鋼帶和鋼管要發生接觸，最終鋼帶將鋼管貼緊完成打捆動作，因此應在鋼帶和鋼管之間添加接觸力，否則鋼帶和鋼管之間會發生干涉，無法完成整個動作仿真。鋼帶與鋼管包之間只要完成與六個邊角鋼管的接觸就可以保證貼緊六個邊的所有鋼管，因此根據鋼管包的邊長計算出與六個邊角鋼管相接觸的鋼帶段即可[9]，如圖7所示。

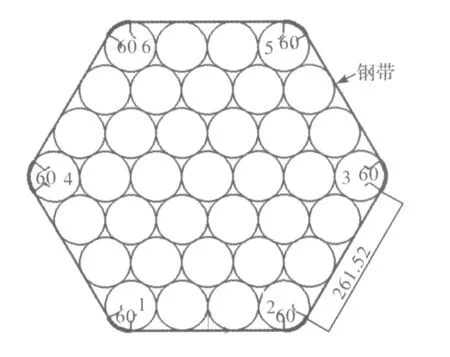
圖7 邊角鋼管示意圖

在soildworks中完成了對新型打捆機械手的三維建模后，將三維模型導入ADAMS中，并完成對主要零部件材料的定義。在ADAMS中用轉動副和轉動驅動的形式來代替伺服電機模擬打捆機械手的運行。由離散法建立的鋼帶模型兩端需要與兩側的末端抓取機構同步運動，完成最終的打捆動作，這里將兩端抓取機構和兩端鋼帶段之間建立固定關系，以模擬實際運行中夾持的動作[10、11]。最終仿真結果如圖8所示。

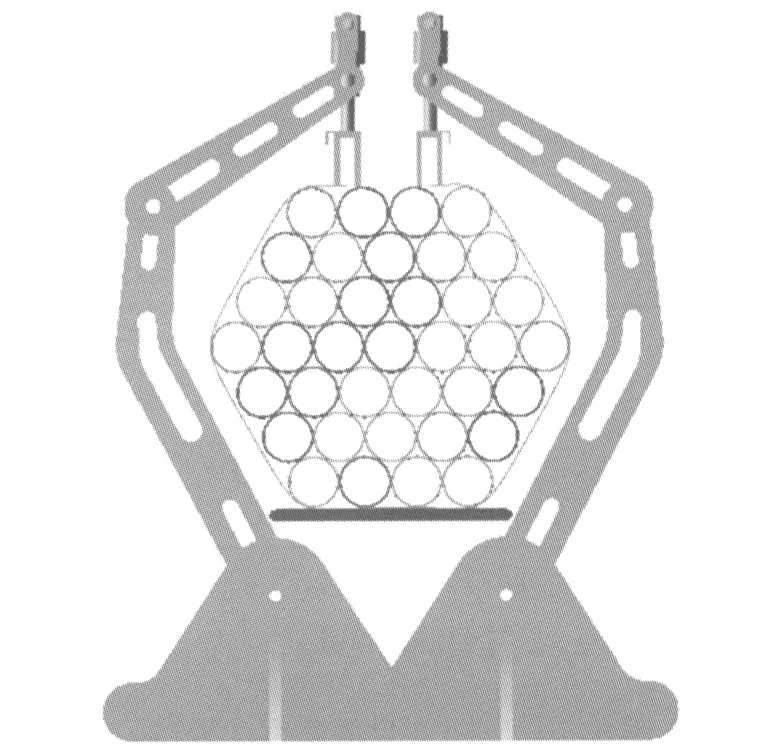
圖8 新型打捆設備三維仿真模型

2.2 基于ADAMS的新型打捆機械手仿真分析

ADAMS是專門用于機械系統動態仿真分析軟件，具有強大的數值分析和求解功能，可以對系統進行運動學和動力學的深入分析，其結果可以用動畫和圖表等形式展現出來，方便更加直觀的讀取所需數據。

2.2.1 基于D-H法的關節驅動函數設計

在參考文獻[2]中對機構運動進行了基于D-H法的運動學反解計算，得到了在MATLAB中計算出的各關節轉角，針對于φ88.9 mm型鋼管包模型，三個關節轉過的角度分別125.22°，-55.71°，-110.49°,利用STEP函數結合D-H法求出的關節角度編寫出六個關節的轉角函數。

(1)

根據式(1)中的六個STEP函數，在Adams中完成關節驅動函數的設計。

2.2.2 打捆機械手仿真結果的處理

在ADAMS/PostProcessor后處理模塊中對機構仿真結果進行分析，將機構仿真運行后的參數輸出為曲線圖表的形式，通過這些曲線圖可以直觀地觀察到各個仿真參數與運行時間之間的關系。因為左右兩側機械臂的運動相同，因此本文只研究右側三機械臂關節的運行結果。

(1)關節角速度-時間圖像。關節角速度是在對機器人進行運動學分析時非常重要的參數，因此在對打捆機械手進行仿真分析后需要對各關節的角速度進行深入分析。在后處理模塊得到各關節z方向旋轉角速度-時間圖像如9所示。

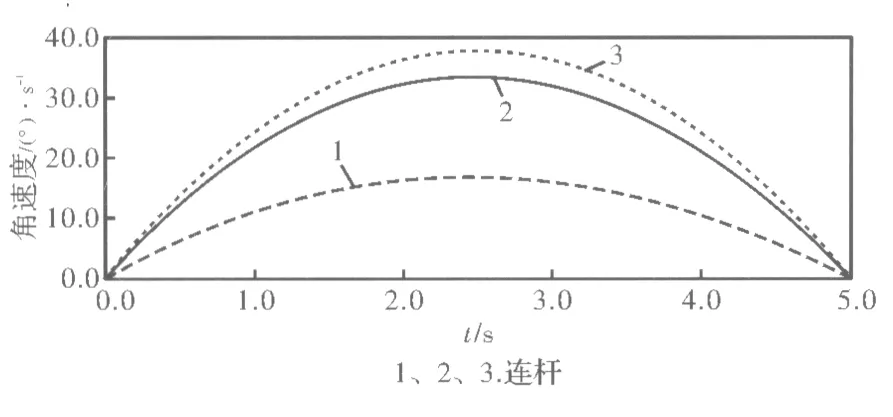
圖9 三連桿關節角速度曲線圖

由圖9中可得三個關節的角速度曲線運行的比較平穩，打捆過程中機械臂運行軌跡合理，未觸碰到鋼管，運行中三機械臂相互之間也未發生干涉，且最終完成了對鋼管包的打捆，因此由運動學公式所求得的運動規律符合實際的任務要求。三個關節角速度都在2.5 s時達到最大值，在數值上最大值分別為37.64 (°)/s、17.01 (°)/s、33.38 (°)/s，平均速度分別為24.97 (°)/s、11.28 (°)/s、22.14 (°)/s，為后續對桿長進行優化提供了所需數據。

(2)關節角加速度-時間圖像。關節角加速度是在對機器人進行運動學分析時不可或缺的重要參數，可以直觀地反映各關節的運動特性，角加速度曲線的變化也可以體現出機構的振動情況，對于機構的整體運行情況有著重要意義。各關節的角加速度圖像如圖10所示。

圖10 末端執行桿關節角加速度

對各關節角加速度圖像進行分析可以得到，角加速度整體變化較為穩定，雖然初始階段都有一定的突變，但在此前已經完成對于鋼帶的抓取，并不影響整個機械手的打捆任務，且運行曲線末端并沒有波動現象。對整個機械手各關節的速度與加速度的分析可知，由D-H法編制的關節驅動函數比較適合整個機械手的打捆任務，而且運行過程也沒有較大的振動，符合預期目標[11]。

2.2.3 運動學方程的驗證

參考文獻[2]中的運動學分析對打捆機械手末端位移與各個關節變量之間的關系進行了理論驗證，進而可以根據ADAMS的仿真和后處理功能，進一步對打捆機械手運動學方程的解進行驗證。根據運動學公式的理論推導過程，末端抓取機構z方向的位移始終為零，因此只要已知各關節任意時刻的θ′角就可以求出末端抓取機構的位姿px、py。在Adams中添加各關節的轉角和末端抓取機構的橫縱坐標變化到同一張曲線圖，如圖11所示。

圖11 各關節轉角與機械手末端位移曲線圖

如圖11中所示，橫軸表示時間，左縱坐標為關節旋轉角度，右縱坐標為末端抓取機構的位移，從圖中既可以讀出各關節的旋轉角度也可以讀出末端抓取機構的位姿。這樣就可以利用圖11的數據來驗證運動學方程的正確性，即在仿真的任一時刻，都可以利用各關節旋轉角求出末端位姿，也可以利用末端位姿求出各關節旋轉角。例如在2 s時，φ1=-44.16°，φ2=19.96°，φ3=39.16°，px=685.93 mm，py=338.43 mm，可得θ1′=3.6°，θ2′=81.03°，θ3′=75.95°，進而求得px=683.27 mm，py=337.15 mm，仿真值與理論值誤差在允許范圍內。通過對圖11的分析可知，D-H法建立的運動學公式是正確的，符合實際情況[2、12]。

2.2.4 打捆機械手關節驅動力矩分析

對打捆機械手進行仿真運行后可以在Adams/PostProcessor中讀出各關節驅動力矩的變化。圖12是在忽略關節運動副間摩擦力的前提下，關節驅動力隨時間的變化曲線，通過對關節驅動力的分析，可以為關節驅動部件的選型提供可靠依據。

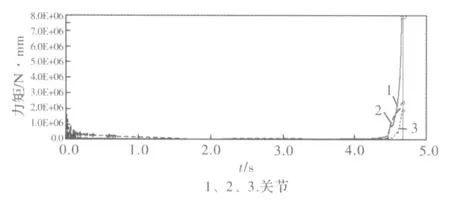
圖12 三關節驅動力矩曲線圖

圖12中橫軸表示時間，縱軸表示各關節的驅動力矩值，圖12中各關節在初始階段都有一定的波動現象，是設備受到的慣性力引起的沖擊。由參考文獻[2]中的分析可知，新型打捆機械手驅動部件是根據靜力學分析進行初步選型的，選型時的參數多數是經估算得到的，會造成一定的誤差，因此應根據仿真時的具體數值選出更為適合打捆設備的驅動部件，由圖中可以讀出各關節的最大力矩值。將兩套設備打捆各自最大包型時的各關節最大力矩值匯總到表3中，為后續驅動部件的進一步選型提供了精確的數據參考。

表3 各關節最大力矩值

3 結論

本文以外徑φ88.9 mm的六角鋼管包作為主要研究對象，針對設計出的打捆機械手簡圖，使用Soildworks和Adams聯合建模，通過新型鋼管打捆機械手的三維實體模型，在Adams軟件中利用建立的運動函數對模型進行了仿真分析，仿真過程中各桿件運行平穩，且相互之間無干涉，通過關節驅動函數的作用最終完成對鋼管包的打捆。通過仿真實驗，驗證了機械結構和運動學驅動函數的合理性，根據仿真結果的各關節力矩變化，為各關節驅動部件的選型提供了參考數據。