打磨工業機器人軌跡規劃仿真

田國富，鄭博濤

(沈陽工業大學 機械工程學院，遼寧 沈陽 110870)

0 前言

傳統方式加工出來的零件往往都有飛邊、毛刺等表面缺陷，為了得到最終的產品還要對這些缺陷進行打磨處理[1]。當前，我國還是主要以人工方式來打磨工件，這樣不僅生產效率低、工件表面一致性差，還會由于打磨環境惡劣對工人的健康造成影響。隨著工業機器人技術的不斷突破，未來使用機器人代替人工打磨就成了趨勢，為了研究打磨機器人的軌跡規劃，本文以FANUC公司的R-2000iB/165型號機器人為打磨設備，通過使用MATLAB軟件中的機器人工具箱對打磨軌跡進行規劃研究。

1 機器人坐標系及D-H參數

R-2000iB/165(圖1)是六自由度工業機器人，由6個旋轉關節及連桿組成，根據機器人的結構，通過D-H法建立機器人坐標系(圖2)。

圖2 機器人連桿坐標系

使用參考文獻[1]中的方法確定D-H參數見表1，關節轉角θi、連桿扭角αi-1、連桿長度ai-1和連桿偏距di[2]。

表1 機器人D-H參數

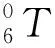
2 機器人三維建模

通過調用MATLAB中機器人工具箱中的函數[3-6]，對R-2000iB/165機器人進行三維建模，具體的MATLAB程序如圖3所示。

圖3 機器人三維建模

其中Link函數中的參數分別為連桿扭角、桿長、關節轉角、連桿偏距與使用標準的D-H參數，調用robot函數將所有的連桿連接起來構成一個整體，調用drivebot函數彈出機器人關節驅動器如圖4所示，通過滑動滑塊即可將機器人運動到指定的位姿。

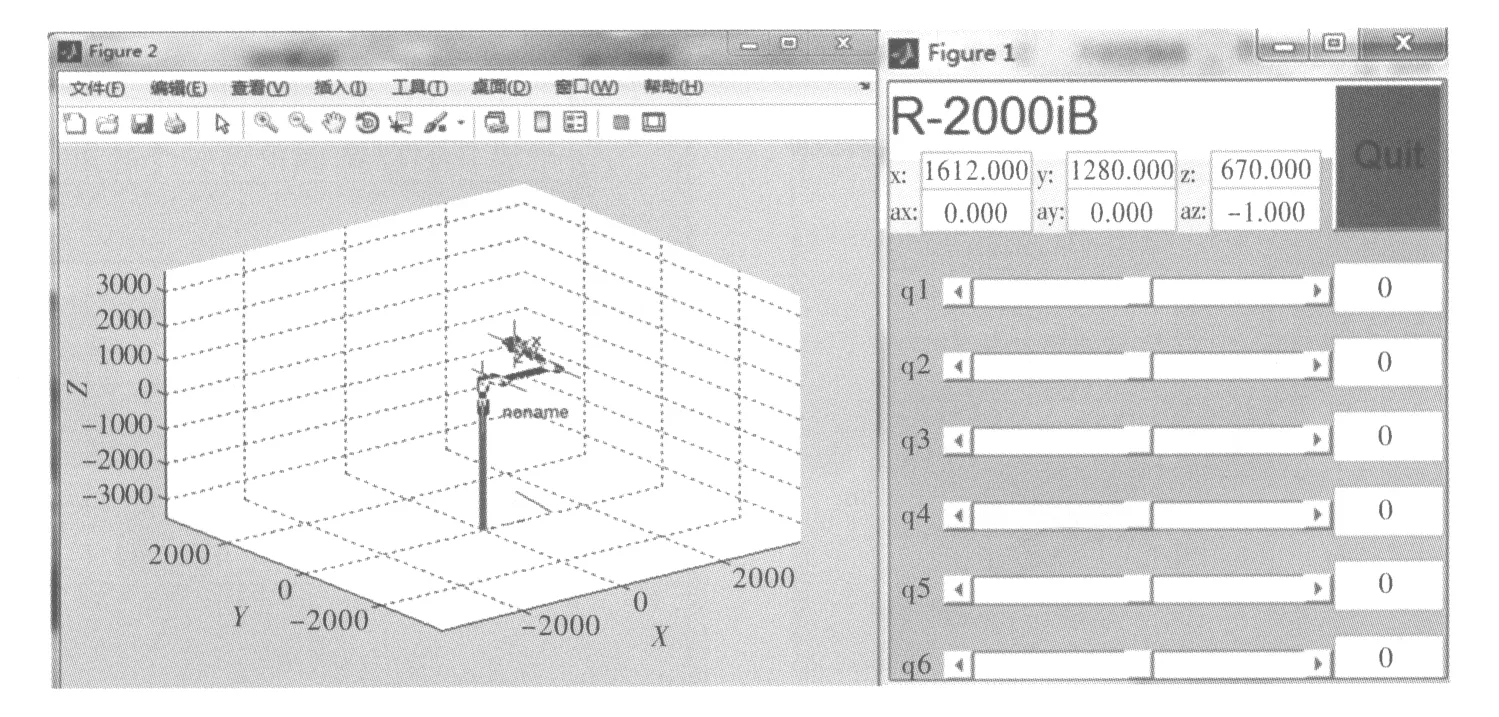
圖4 機器人三維模型

建立完機器人三維模型建立后便可進行機器人軌跡的規劃研究。

3 基于Robotics Toolbox的軌跡規劃仿真

軌跡規劃包括關節空間規劃與笛卡爾空間規劃兩種軌跡規劃，不同空間的軌跡規劃具有不同的優缺點。關節空間軌跡規劃具有計算量小、不會出現奇異現象的優點，但機器人末端在空間中的運動軌跡是未知的。笛卡爾空間軌跡規劃具有運動路徑直觀的優點，但難以確定在運動過程中是否會發生奇異的現象。要使機器人能夠平穩的運動，不論哪種規劃，都要求運動軌跡是光滑連續的[7-10]。

3.1 關節空間軌跡規劃

為了在關節空間中規劃機器人的運行軌跡，需要設定下運動初始點與終止點，取初始點q1=[0 0 0 0 0 0]，終止點q2=[pi/4 pi/5 pi/6 pi/4 pi/3 pi/5]，設定運動時間為2 s，為了方便僅對關節1和關節2進行研究，其MATLAB程序如圖5所示。

圖5 關節空間軌跡規劃程序

調用jtraj函數可對關節空間進行五次多項式插值，調用plot(t，q(:，i))、plot(t，qd(:，i))和 plot(t，qdd(:，i))可分別得到各個關節的角位移曲線、角速度曲線和角加速度曲線。運行程序即可得到關節1、2的角位移、角速度和角加速度曲線，如圖6所示。

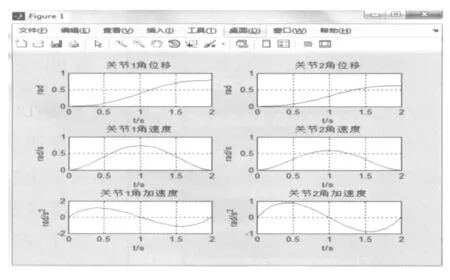
圖6 關節角位移、速度、加速度曲線

觀察圖6可以發現機器人在運動過程中角位移、速度、加速度曲線都光滑平穩，說明機器人各個連桿沒有發生錯位的現象，角位移從初始位置隨著時間運動到終止點的位置，角速度從零運動1 s左右達到最大速度后又逐漸減為零，角加速度先正后負正好對應上速度先增大后減小，因此該關節空間軌跡規劃是較為合理的。

3.2 笛卡爾空間軌跡規劃

本文以空間直線為例進行軌跡規劃，在笛卡爾空間進行軌跡規劃時同樣需要設定初始點與終止點，取初始點T1=transl(78，171,1953，093,123，915)，終止點T2=(387，872,1920，068,880，126)，運動時間也設定為2秒，軌跡規劃MATLAB程序如圖7所示。

圖7 笛卡爾空間軌跡規劃程序

調用工具箱中的ctraj函數可以在笛卡爾空間軌跡機器人運動軌跡，調用plot(t，Tj(：，i))函數可以得出機械臂末端的三維空間坐標，如圖8所示。

圖8 機器人末端三維坐標

通過程序語句plot3(Tj(：，1)，Tj(：，2)，Tj(：，3))即可畫出機械臂末端在空間中的運行軌跡，如圖9所示。

圖9 機器人末端空間運動軌跡

為了確定該軌跡規劃是否合理，還需要觀察機器人在運動過程中各個關節轉角的變化情況，通過如圖10中的MATLAB程序就可得到關節轉角的變化曲線如圖11所示。

圖10 求各個關節角的MATLAB程序

圖11 關節角度變化曲線

觀察圖11可以發現在笛卡爾空間進行軌跡規劃時，各個關節轉角沒有發生突變，說明規劃是合理的。

4 總結

利用MATLAB軟件建立了機器人三維模型，在關節空間與笛卡爾空間進行了軌跡規劃，通過軌跡仿真可以得出機器人的運動是平穩連續的，在機器人從初始位置(或開機位置)運動到打磨初始點時，由于這個過程不需要有精確的行走路線，為了節省時間，可對這個過程進行關節空間軌跡規劃。當從打磨初始點運動到打磨終止點時需要機器人沿著精確到路徑移動，這時就需要在笛卡爾空間進行軌跡規劃，這樣不僅提高了打磨效率，還提高了打磨質量。