兩參數Cauchy分布的參數估計方法
顧蓓青,王蓉華,徐曉嶺
(1.上海對外經貿大學 統計與信息學院,上海 201620;2.上海師范大學 數理學院,上海200234)
0 引言
設隨機變量X服從位置參數μ、刻度參數λ的兩參數Cauchy分布(記為C(μ,λ)),其密度函數f(x)和分布函數F(x)分別為:
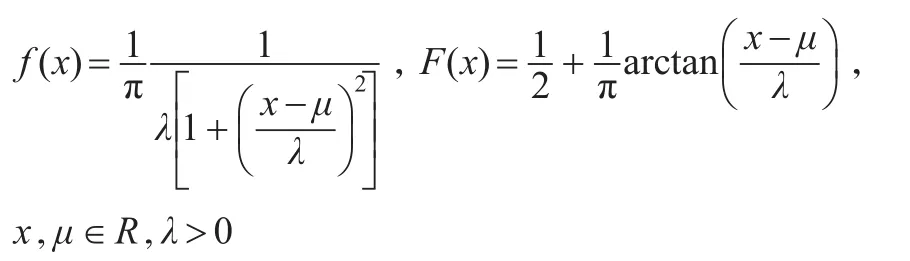
Cauchy分布因其期望和方差都不存在而受到廣泛關注,其在物理學等眾多領域也有著十分重要的應用價值。關于Cauchy分布的一些特別性質,可查閱文獻[1-3]。同時,也有很多文獻對Cauchy分布的參數估計問題進行了一些研究。文獻[4]討論了矩估計和極大似然估計等一些常用的點估計方法對Cauchy分布C(μ,1)并不適用,從而提出了利用中位數的方法得到參數μ的估計。文獻[5]通過局部矩估計的方法得到Cauchy分布C(0,λ)的參數λ的點估計與區間估計,同時也說明了該方法的局限性。文獻[6]給出了Cauchy分布C(μ,λ)的兩個參數的分位數估計。文獻[7]在全樣本場合下研究了兩參數Cauchy分布C(μ,λ)的點估計與區間估計。
本文給出了兩參數Cauchy分布C(μ,λ)在全樣本場合下參數的區間估計和定數截尾場合下參數的點估計與區間估計方法,并通過Monte-Carlo模擬考察了點估計與區間估計的精度。
1 全樣本場合下兩個參數的區間估計
設X1,X2,…,Xn為來自總體X~C(μ,λ)的一個容量為n的簡單隨機樣本,其樣本觀察值記為x1,x2,…,xn,次序統 計 量 記 為X(1)≤X(2)≤ … ≤X(n),其 次 序 觀 察 值 記 為則Y~C(0,1),而Y1,Y2,…,Yn與來自標準 Cauchy 分布C(0,1)總體的容量為n的一個簡單隨機樣本同分布,將其從小到大排序記為:Y(1),Y(2),…,Y(n)。
1.1 參數μ的區間估計
令μ的函數
其中,若n為偶數若n為奇數時,
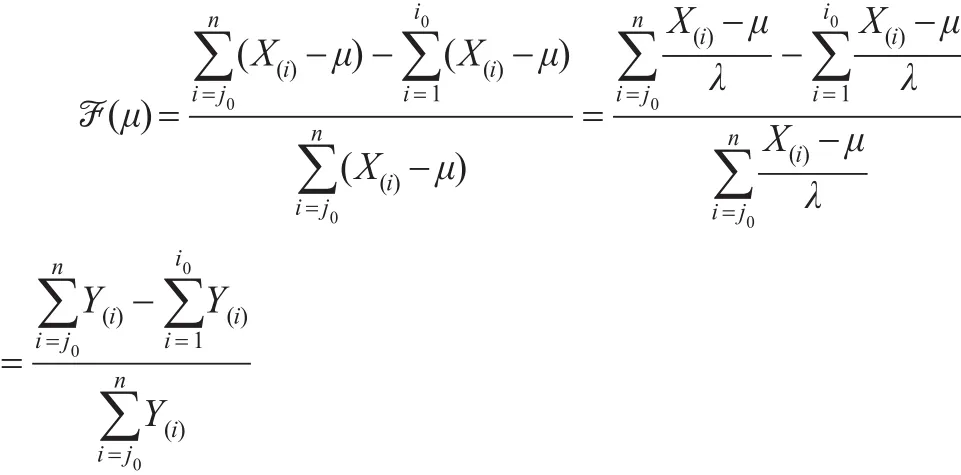
于是?(μ)是僅含有參數μ的樞軸量,又?(μ)為μ的嚴格單調增函數,且:
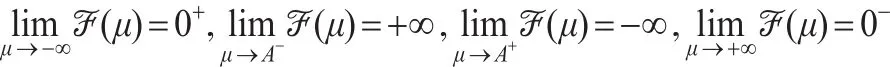
由此,給定顯著性水平α,樞軸量)的上側1-α/2,α/2分位數記為和,通過Monte-Carlo模擬可以得到不同樣本容量所對應的樞軸量)的上側分位數值。從而,參數μ的置信水平1-α的區間估計為:

1.2 參數λ的區間估計
構造如下僅含有參數λ的樞軸量:
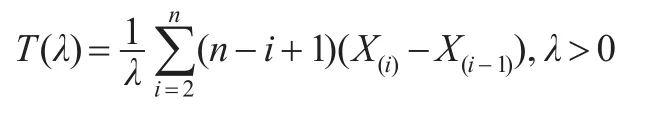
又:
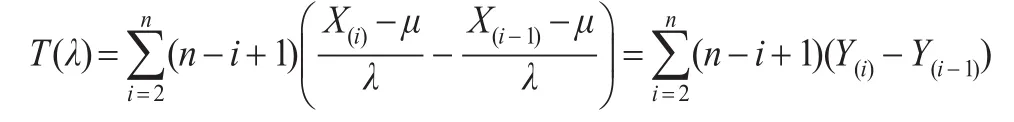
于是T(λ)是僅含有參數λ的樞軸量,又T(λ)是λ的嚴格單調減函數。
給定顯著性水平α,樞軸量T(λ)的上側1-α/2,α/2分位數分別記為T1-α/2和,通過Monte-Carlo模擬可以得到不同樣本容量所對應的樞軸量T(λ)的上側分位數值。從而,參數λ的置信水平1-α的區間估計為:
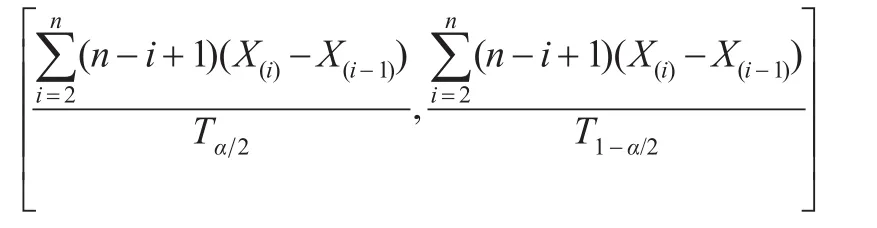
1.3 模擬分析
給定置信水平1-α=0.90 ,取樣本容量n=10(5)30 ,參數真值取為μ=-5,0,5,λ=0.5,通過1000次Monte-Carlo模擬得參數μ,λ的區間估計的平均下限、平均上限和平均區間長度,同時統計1000次模擬所得的區間估計包含參數真值的次數,結果如表1所示,從中可以看到上述所給出的求區間估計的方法是可行的。
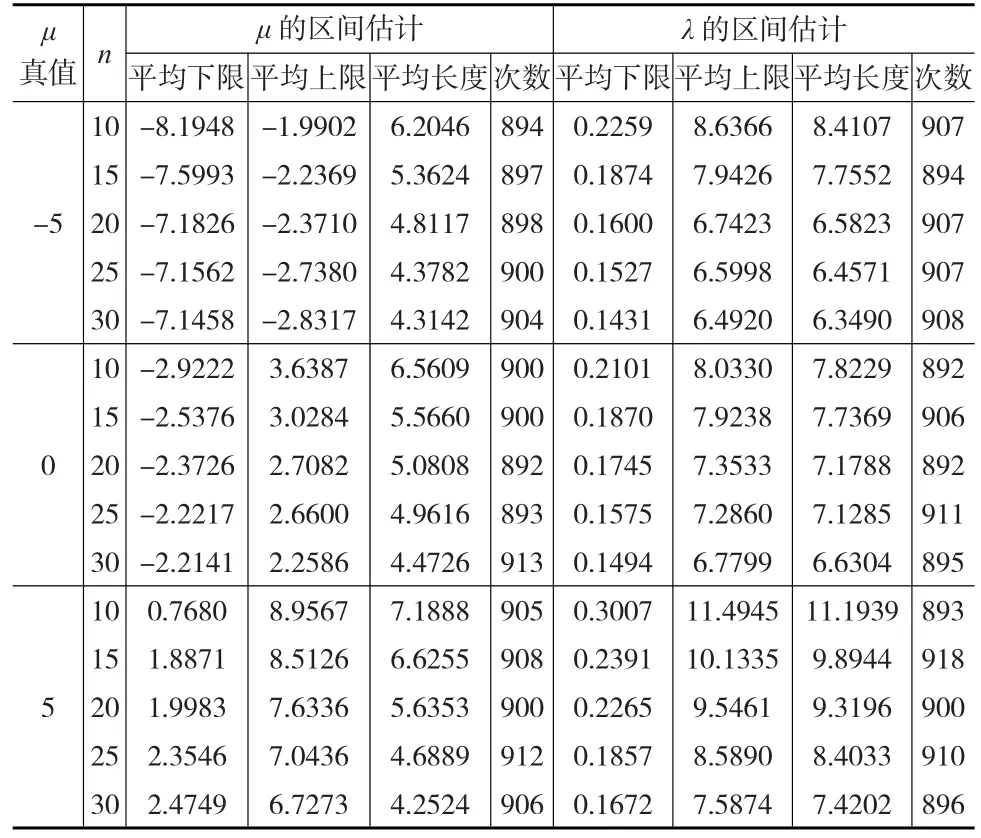
表1 參數μ,λ的區間估計
2 定數截尾場合下兩個參數的點估計與區間估計
設X(1),X(2),…,X(r)為來自總體X~C(μ,λ)的一個容量為n的前r個次序統計量,其次序觀察值記為則Y~C(0,1),而Y(1),Y(2),…,Y(r)與來自標準 Cauchy分布C(0,1)總體的容量為n的前r個次序統計量同分布。
注意到,如給定0<p<1,由文獻[8]可知樣本的p分位數X*(p)可定義為:
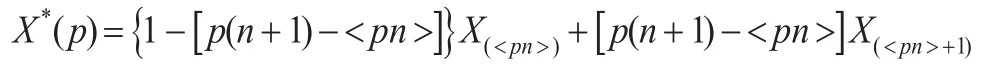
其中,<pn>為pn的整數部分。
2.1 參數的點估計
進而參數μ的點估計為:
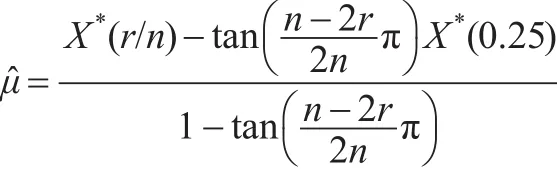
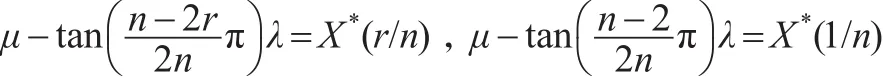
則參數λ的點估計為:
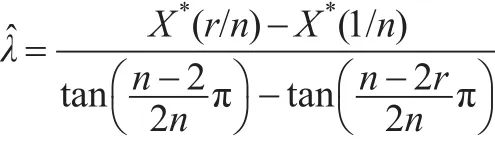
進而參數μ的點估計為:
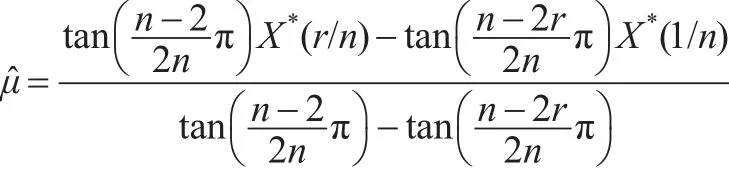
其中[]表示取整函數。
由于該情況下的樣本量較少,估計的效果不甚理想,會受到樣本值的影響,在此僅舉一模擬算例說明該方法的應用:取n=20,r=4,參數真值取μ=0,λ=1,通過Monte-Carlo模擬產生的一組截尾樣本為-4.2946,-4.2491,-1.9168,-0.92,則?=0.0207 ,?=0.6835 。
取樣本容量n=10(5)30以及定數截尾數r,參數真值取μ=0,λ=1,通過10000次模擬得到參數μ,λ的點估計的均值與均方差,結果列于表2。
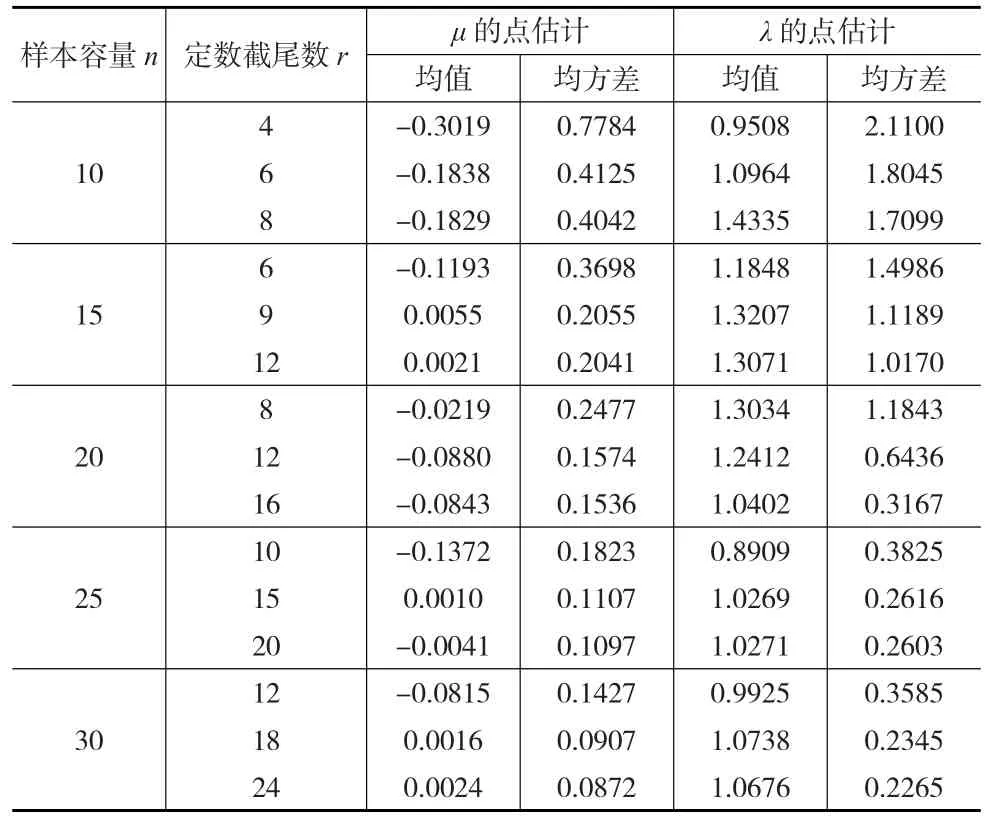
表2 參數μ,λ的點估計
2.2 參數的區間估計
2.2.1 參數μ的區間估計
令μ的函數
其中,若r為偶數若n為奇數時,
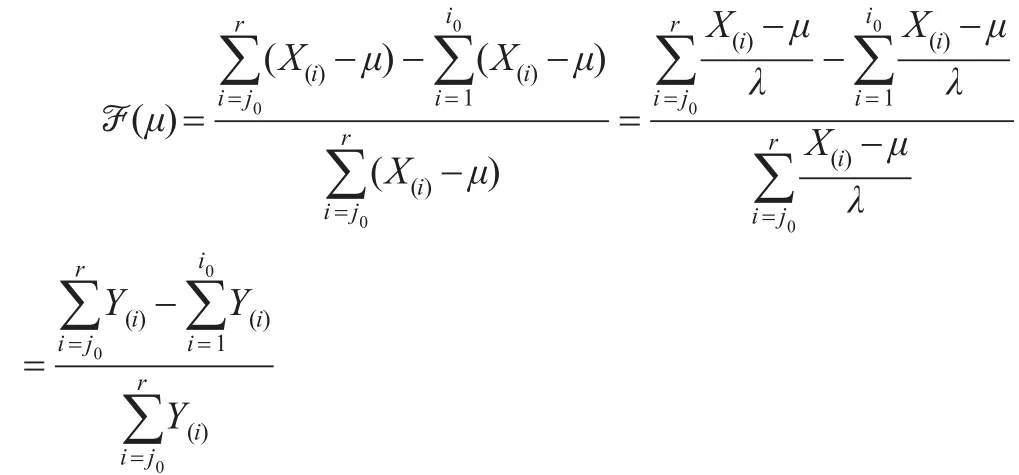
于是?(μ)是僅含有參數μ的樞軸量,又?(μ)為μ的嚴格單調增函數,且:
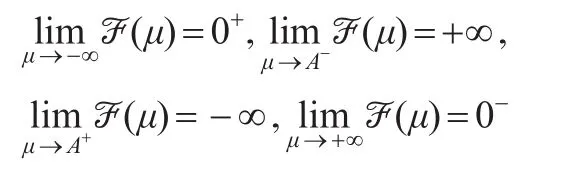
由此,給定顯著性水平α,樞軸量)的上側1-α/2,α/2分位數記為和,通過Monte-Carlo模擬可以得到不同樣本容量n和定數截尾數r所對應的樞軸量?(μ)的上側分位數值。從而,參數μ的置信水平1-α的區間估計為:
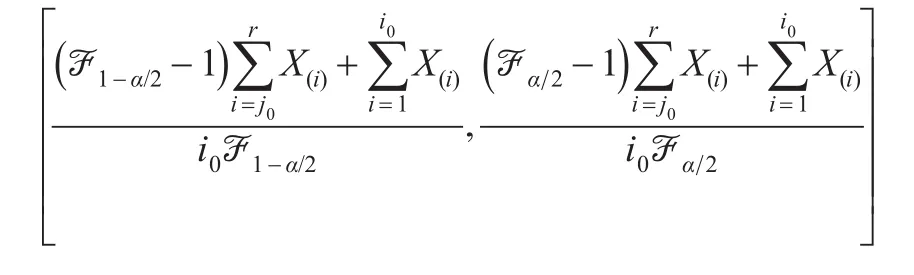
2.2.2 參數λ的區間估計
構造如下僅含有參數λ的樞軸量:
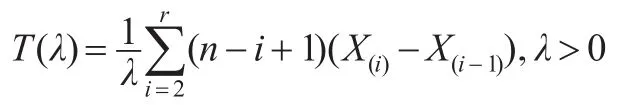
又:
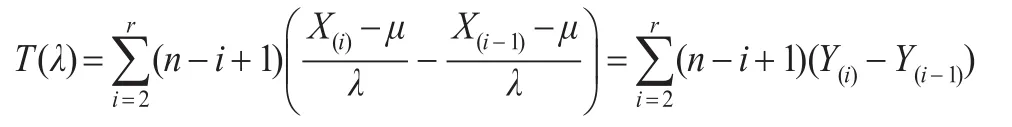
于是T(λ)是僅含有參數λ的樞軸量,又T(λ)是λ的嚴格單調減函數。
給定顯著性水平α,樞軸量T(λ)的上側1-α/2,α/2的分位數分別記為和,通過Monte-Carlo模擬可以得到不同樣本容量n和定數截尾數r所對應的樞軸量T(λ)的上側分位數值。從而,參數λ的置信水平1-α的區間估計為:

2.2.3 模擬分析
給定置信水平1-α=0.90,取樣本容量n和定數截尾數r,參數真值取為μ=1,λ=1,通過1000次Monte-Carlo模擬得參數μ,λ的區間估計的平均下限、平均上限和平均長度,同時統計1000次模擬所得的區間估計包含參數真值的次數,結果如表3所示。
3 算例分析
例1:文獻[5]提供了如下算例,取樣本容量n=10,刻度參數λ的真值取為5,通過Monte-Carlo模擬產生10個服從C(0,λ)分布的隨機數如下:
2.3008 ,3.9756,-6.4165,11.9341,16.4812,-0.2428,-7.9044,-6.3136,14.5784,-1.9155
文獻[5]得到了參數λ的局部矩估計為:?=5.0953;利用文獻[7]的方法可以得到:μ的點估計為?=X*(0.5)=1.029 ,λ的點估計為=X*(0.5)-X*(0.25)=7.3426 ,=X*(0.75)-X*(0.5)=10.9051,=5.6939;利用本文方法可以得到:在置信水平1-α=0.90下,μ的區間估計為[- 4.4215,9.0711] ,λ的區間估計為[0 . 1705,6.5199] 。
例2:取樣本容量n=30,定數截尾數r=26,通過Monte-Carlo模擬產生一組服從C(3,2)分布的隨機數如下:
-3.71106,-2.40515,-1.21566,-0.424847,0.296015,0.518243,0.744813,1.49002,1.90678,1.98354,1.99277,2.27703,2.47186,2.86832,2.8724,3.02303,3.27706,3.3678,3.69184,4.29,4.54302,4.63784,4.91429,5.53984,7.47502,8.44948
利用本文方法可以得到:μ的點估計為?=X*(0.5)=2.9477 ,λ的點估計為?=X*(0.75)-X*(0.5)=1.9666 ,在置信水平1-α=0.90下,μ的區間估計為[2 . 2743,4.4547] ,λ的區間估計為[0 .0383,2.0716] 。
4 結論
針對兩參數Cauchy分布C(μ,λ),在全樣本場合下通過構造樞軸量分別得到參數μ和λ的區間估計,通過Monte-Carlo模擬考察了區間估計的精度,從模擬結果來看,該區間估計方法具有可行性。此外,在定數截尾場合下,通過分位數得到參數μ和λ的點估計,并利用樞軸量法得到參數μ和λ的區間估計,同時通過Monte-Carlo模擬分別考察了點估計與區間估計的精度,從模擬結果來看,點估計和區間估計的方法都是可行的。最后,通過兩個模擬算例說明了本文方法的應用。

