隱狀態個數未知的隱馬爾可夫0-1分布的貝葉斯推斷

李 勇,劉鶴飛

（曲靖師范學院a.信息工程學院；b.數學與統計學院，云南曲靖 655011）

0 引言

隱馬爾可夫模型是一種基于隨機過程的統計學模型。隱馬爾可夫模型由兩個隨機過程構成，一個是狀態轉移序列、一條單純的馬爾可夫鏈；另一個是與狀態對應的觀測序列。在實際問題的研究中，只能看到觀測序列的集合，而不能看到狀態序列集合。也就是說，模型的狀態隱藏在觀測序列中，因此稱之為“隱”馬爾可夫模型[1]。隱馬爾可夫模型的研究內容就是通過可觀測的變量序列集合去推斷不可觀測的狀態序列轉移特征及每個狀態下的分布信息。

近年來，馬爾可夫模型在許多領域都有了極大的發展和廣泛的應用。例如，在圖像處理領域，沈杰等[2]利用隱馬爾可夫模型改進了人臉識別技術；在語音識別領域，魏明哲[3]通過隱馬爾可夫模型的分類識別提高了語音識別的效果；在生物醫學領域，劉青等[4]通過隱馬爾可夫模型實現基因識別系統的設計。在經濟金融領域，孫鵬飛等[5]利用隱馬爾可夫模型來擬合美元LIBOR相對美聯儲基準利率的變動情況。

雖然近年來關于隱馬爾科夫模型的研究成果比較豐富，但是由于隱馬爾可夫模型的復雜性，大多數研究都是關于隱馬爾科夫模型的應用性研究，對于隱馬爾科夫模型的純理論性研究非常少。本文在已有的關于隱馬爾科夫模型理論研究成果的基礎上，研究隱狀態個數未知條件下的隱馬爾可夫0-1分布模型。首先利用可逆跳躍MCMC[6]方法對未知的隱狀態個數進行貝葉斯模型選擇；確定隱狀態個數之后再用MCMC算法估計隱馬爾可夫0-1分布的參數；最后生成觀測數據集，實證模擬檢驗該方法的推斷效果。

1 模型描述

觀測變量yit來自0-1分布，其中i=1，2，...，N是觀測對象，t=1，2，...，T是觀測時點。Zit是系統觀測對象在第t個觀測時點的隱狀態，其取值范圍為{1，2，...，K}，稱為K個隱狀態的隱馬爾可夫模型。

假設模型不可觀測的隱式鏈滿足以下馬爾可夫鏈條件：P（Zit=s│Zi1，Zi2，...，Zi（t-1）=u）=P（Zit=s│Zi（t-1）=u）=aus

其中：

u=1，2，...，K;s=1，2，...，K;i=1，2，...，N;t=2，3，...，T。

則aus是從前一個時點的隱狀態u向后一個時點的隱狀態s的轉移概率。全部可能的隱狀態轉移概率構成一個矩陣，稱為隱狀態轉移概率矩陣，記為：

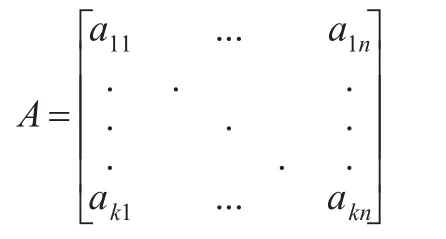
隱狀態轉移概率矩陣的每一行之和為1。

在給定隱狀態的條件下，隱馬爾可夫0-1分布的觀測變量定義為：

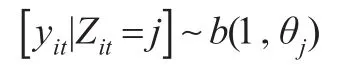
其中θj是第j個隱狀態下0-1分布的參數，yit是0-1分布的觀測度量，其取值僅為0或1。

2 貝葉斯推斷

2.1 推斷原理

記θ為不同隱狀態下0-1分布的參數集合，即θ=（θ1，θ1，...，θk）。 則 該 模 型 的 貝 葉 斯 推 斷 問 題 為P（K，Z，A，θ|Y），就是要根據觀測度量的信息推斷出模型的因狀態個數K，隱狀態集合信息Z，轉移概率矩陣A，以及不同隱狀態下0-1分布的參數θ。利用可逆跳躍馬爾可夫鏈蒙特卡羅算法推斷的具體執行步驟為：

（1）更新隱狀態Z；

（2）更新隱狀態轉移概率矩陣A；

（3）更新0-1分布的參數θ；

（4）將一個隱狀態分裂為兩個，或者將兩個隱狀態合并成一個。

步驟（1）至步驟（3）中每一步更新參數都是普通的馬爾可夫鏈蒙特卡羅算法，主要利用Gibbs抽樣[7]和MH算法[8]從相關參數的全條件后分布抽樣即可。步驟（4）是可逆跳躍步，在這一步中，允許以pk和qk=1-pk的概率增加或者減少一個隱狀態。一般情況下，使增加一個隱狀態和減少一個隱狀態的概率相等，即pk=qk=0.5，但是q2=pmax=0除外。其中，q2=0表示隱狀態個數為2時，再減少隱狀態的概率為0；pmax=0表示隱狀態達到設定的最大值時，再增加隱狀態的概率為0；當隱狀態為其他值時，增加一個隱狀態和減少一個隱狀態的概率是相等的，都是0.5。

2.2 先驗分布

貝葉斯推斷中，所有參數都看成是隨機變量，所以，在進行貝葉斯推斷時，要先為每一個參數選擇一個合適的先驗分布。本文借鑒已有的研究經驗[9]，為各個參數選取的先驗分布如下：

Ak～D（α，α，...，α）

θj～U（0，1）

其中，Ak表示隱狀態轉移概率矩陣的第k行，D表示狄尼克萊分布，α是狄尼克萊分布的超參數。θj表示第j個隱狀態下0-1分布的參數，為其選擇的先驗分布是（0，1）上的均勻分布。

2.3 全條件后驗分布

貝葉斯后驗推斷主要是利用樣本信息和參數的先驗信息對模型進行推斷。對于本文來說，即P（K，Z，A，θ|Y）。由于這個后驗分布的復雜性，本文利用馬爾可夫鏈蒙特卡羅方法來對后驗分布進行模擬，這就需要推導相關參數的全條件后驗分布。

隱狀態Z的全條件后驗分布P（Z|A，θ，Y）為：

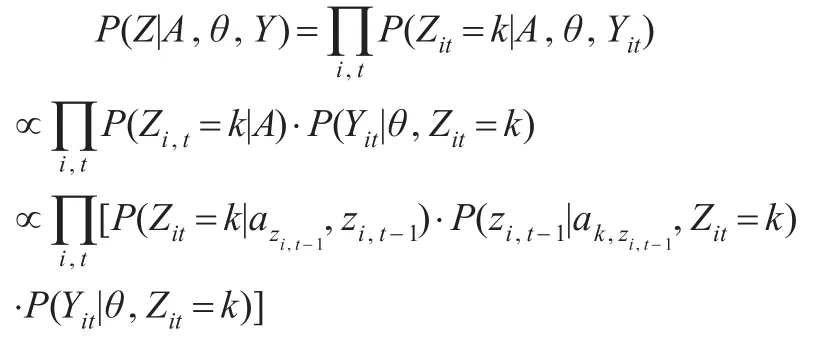
也即：

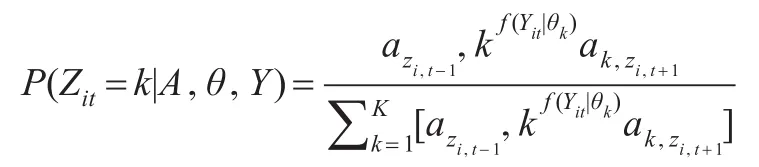
其中，fk（Yt|θk）是觀測變量在隱狀態k下的似然函數。

由于隱狀態轉移概率只與隱狀態的取值情況有關，所以P（A|Y，Z，θ）=P（A|Z），又因為A的每一行元素的先驗分布都是對稱的狄尼克萊分布D（α，α，...，α），所以每一行的全條件后驗分布為：

P（Ak|Z）～D（α+nk1，...，α+nkK）

其中nki是前一個隱狀態為k，后一個隱狀態為i的樣本總個數。

接下來推導0-1分布參數θ的全條件后驗分布。當隱狀態Z確定時，隱狀態轉移概率矩陣A也隨之確定，此時第j個0-1分布的參數θj只與觀測變量Yj有關，即P（θj|Y，A，Z）=P（θj|Yj），其中，Yj是隱狀態為j的觀測變量集合。

由于Yj1，Yj2，...，Yjn～b（1，θj），則Yj～b（nj，θj），也即：

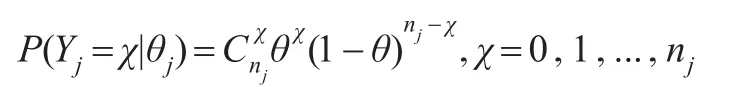
由于θj的先驗分布是U（0，1），則其概率密度函數為：

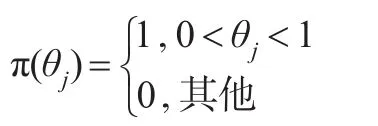
則樣本Yj與參數θj的聯合概率密度函數為：。

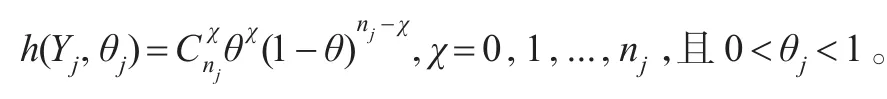
Yj的邊際密度為：

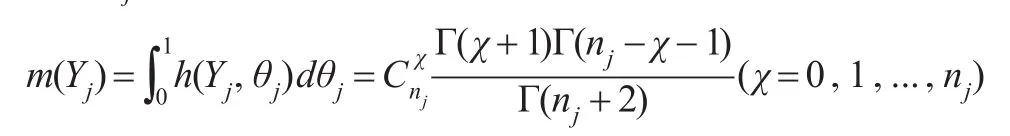
利用貝葉斯公式可得θj的后驗分布：

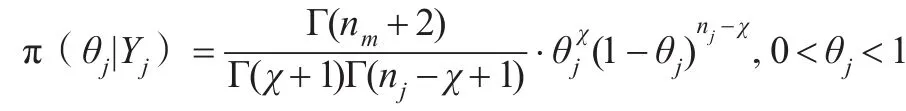
此式是參數為χ+1，nj-χ+1的貝塔分布，即θj的全條件后驗分布為：

θj～Beta（χ+1，nj-χ+1）

2.4 可逆跳躍過程

1995年，Green[7]提出了可逆跳躍馬爾可夫鏈蒙特卡羅算法，該方法通過在可變維參數空間中跳躍式抽樣，實現貝葉斯模型選擇的目的。1997年，Richardson[10]和Green利用可逆跳躍MCMC算法對正態混合模型中未知的混合個數進行選擇。2000年，Robert[11]利用可逆跳躍MCMC算法對隱馬爾可夫正態分布中未知的隱狀態個數進行選擇。本文借鑒以上研究方法，利用可逆跳躍MCMC算法對隱馬爾可夫0-1分布中未知的隱狀態個數進行模型選擇。

可逆跳躍MCMC算法與普通的MCMC算法的主要區別是，在可逆跳躍步，允許未知的隱狀態個數隨機地增加或者減少一個，模型的參數發生相應的變化，最后以一定的概率接受或者拒接這種跳躍。以增加一個隱狀態為例，可逆跳躍步的具體執行方法為：（1）從當前的k個隱狀態中等概率隨機的選擇一個；（2）從預先給定的分布中生成一定數量的隨機數；（3）利用生成的隨機數，根據相應的分解方式，將選中的隱狀態分解成兩個；（4）以概率min（1，M）接受這種跳躍，其中：

M=似然比×先驗比×跳躍比×建議比×雅克比

對于隱馬爾可夫0-1分布來說，假設當前的隱狀態個數為k，則有一個k階的隱狀態轉移概率矩陣，有k個在0～1之間的參數θj。根據可逆跳躍MCMC算法的要求，增加一個隱狀態，需要將k階的隱狀態轉移概率矩陣增加到k+1階，并且增加一個0～1之間的參數θ。將選中的待分解的隱狀態記為j*，將j*分解之后的兩個隱狀態分別記為j1和j2。下面分別介紹生成隨機書分解A和θ的具體方法。

Robert[12]根據矩陣的特征值，提出了一種能保留轉移狀態特征的轉移概率矩陣的分解方法。以k階隱狀態轉移概率矩陣分解為k+1階為例，由于轉移概率矩陣的每一行元素之和為1，因此k階轉移概率矩陣有k（k-1）個自由元素，k+1階轉移概率矩陣有（k+1）k個自由元素。下面介紹如何生成k（k+1）-k（k-1）=2 個隨機數，對k階轉移概率矩陣進行分解。

首先生成t0～Beta（2，2），然后根據以下公式計算r和s:

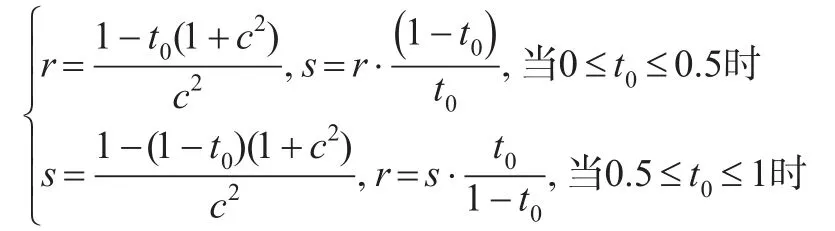
其中，c2是Beta（r，s）的方差，根據經驗，選擇c2=0.3。

再從Beta（r，s）中生成隨機數，使得：

uj～Beta（r，s），j=1，2，...，k且j≠j1，j2

vj～Beta（r，s），j=1，2，...，k且j≠j1，j2

記分裂前的轉移概率矩陣A=aij，i，j=1，2，...，k；分裂后的轉移概率矩陣為B=bij，i，j=1，2，...，k+1,則有：

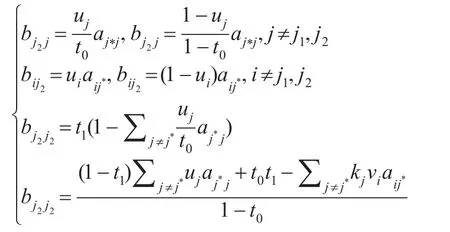
上式中，t0、uj、vj的生成方法已經介紹過了，最后來介紹隨機數t1的生成方法。

令：

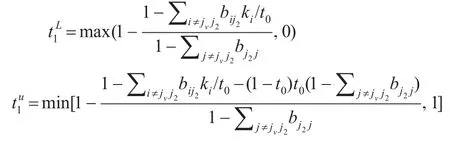
如果＜，則沒有符合條件的t1，隱狀態轉移概率矩陣分解不成功，分解跳躍過程立即停止。如果＜，則在區間[，]上，隨機地選擇一個值作為t1。

以上就是通過生成隨機數，將k階隱狀態轉移概率矩陣分解成k+1階的詳細過程，這種分解方式不僅能保證每行元素之和為1，而且是可逆的，更重要的是能最大限度保留原來的轉移狀態特征。生成隨機數，將0-1分布的參數θj*分解成θj1和θj2的方法比較簡單，只需令ε～U（0，1），θj2=ε*θj*，θj2=（1-ε）*θj*即可。

最后來計算這種分解跳躍的接受概率。因為接受概率為min（1，M），且M=似然比×先驗比×跳躍比×建議比×雅克比。每部分的表達式分別為：

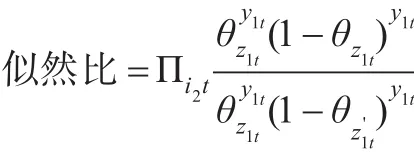
其中，z1t是分解之前第i個觀測對象在第t個觀測點的隱狀態，是分解之后第i個觀測對象在第t個觀測點的隱狀態。

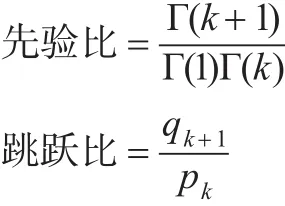
建議比 =[B1，2（t0）ΠjBr，s（uj）ΠjBr，s（vj）]-1

其中，B2，2表示Beta（2,2）分布的密度函數；Br，s表示Beta（r,s）分布的密度函數。

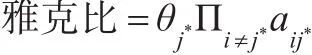
3 實證模擬

根據隱馬爾可夫0-1分布的數學定義，生成一個觀測變量數據集。首先利用可逆跳躍MCMC算法對未知的隱狀態個數進行模型選擇；然后在隱狀態個數已知的情況下利用MCMC算法對模型的參數進行貝葉斯估計；最后將估計結果與模型參數的真實值進行比較，觀察所給方法的推斷效果。

取真實的隱狀態個數k=2，觀測對象個數N=500，觀測時間T=10，轉移概率矩陣兩個0-1分布的參數分別為θ1=0.4，θ2=0.7。

取狄尼克萊分布中的超參數α=1，在使用可逆跳躍MCMC算法時，取迭代總次數為5萬次，去掉前面的3萬次，用后面2萬次的結果來計算未知隱狀態個數的后驗概率。圖1是5萬次迭代過程隱狀態個數的迭代路徑圖，表1（見下頁）是隱狀態個數的后驗概率。

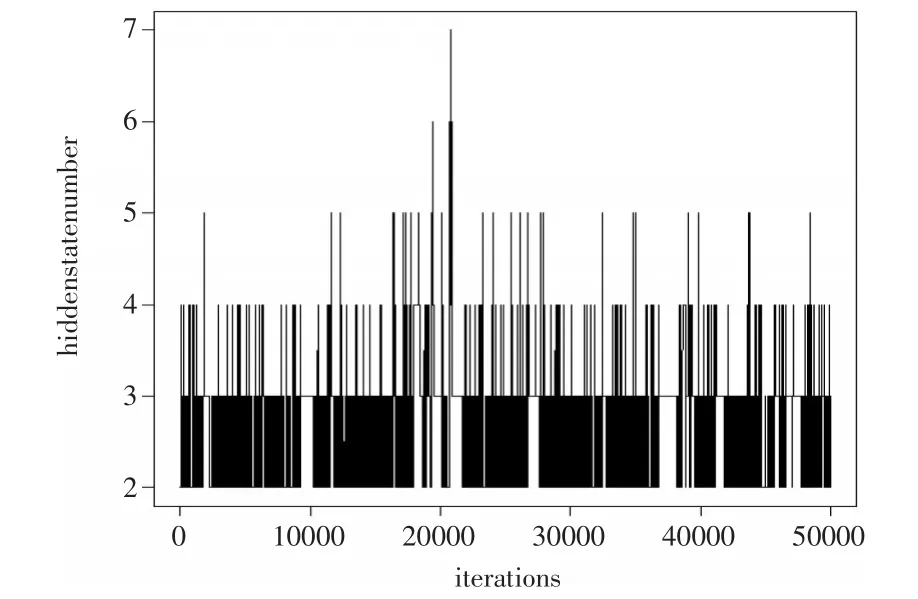
圖1 隱狀態個數迭代路徑圖

表1 隱狀態后驗概率

根據隱狀態個數的后驗概率結果，本文選擇K=2作為未知的隱狀態個數。然后再用MCMC算法取估計隱狀態的轉移概率和每個隱狀態下的0-1分布參數值。超參數取值不變，MCMC算法的迭代總次數為8千次，去掉前面4千次，用后面4千次的后驗均值作為未知參數的估計值，估計結果見表2。

表2 參數估計結果

4 結束語

本文研究了隱狀態個數未知情況下的隱馬爾可夫0-1分布的貝葉斯推斷。首先為模型中的所有參數選擇了合適的先驗分布，并推導出了各參數的全條件后驗分布，然后詳細介紹了利用可逆跳躍MCMC進行模型選擇時，可逆跳躍步的具體執行過程，包括隨機數的生成方式、參數的分解方式、跳躍的接受概率計算公式等。隱狀態個數確定之后，再用普通的MCMC算法估計模型中未知參數的值。最后，將模型的貝葉斯推斷結果與設定的真實模型進行比較，發現利用可逆跳躍MCMC算法選出的隱狀態個數與設定的真實隱狀態個數一致，并且利用MCMC算法計算出的參數的后驗均值也與模型設定的參數的真實值非常接近，這說明，該模型的貝葉斯推斷效果良好。

本文的模型中考慮的是最簡單最常用的0-1分布，0-1分布比較簡單，分布中只含有一個未知參數，但其觀測變量的取值只有0和1兩個值，也導致觀測變量的信息比較單調，所以該模型的推斷也有一定的困難。今后的研究，可以在此基礎上考慮更復雜的分布。