基于凸序列對稱變換非等間距GM（1,1）模型

孔新海，馬 新

（1.廣安職業技術學院 智能制造與能源工程學院，四川 廣安 638000；2.西南科技大學 理學院，四川 綿陽 621010）

0 引言

灰色系統理論自被提出以來，經過幾十年的快速發展，已被廣泛地應用于經濟社會管理、工業企業生產等各個領域。它能夠處理小樣本貧信息問題，是處理這類問題方法體系，特別GM（1,1）模型是灰色系統理論中非常簡潔且應用廣泛的一類預測模型[1]。在應用過程中，為了提高模型精度，很多學者提出了優選初始值、優化灰導數或背景值等一系列的改進方法[2,3]；而針對建模序列的特點，提出了適合單調遞增序列、單調遞減序列或非等間距序列的GM（1,1）建模方法及其優化措施[4-9]。對于具有凹凸性的序列，文獻[10]提出了用軸對稱手段來改變原始序列凹凸性進行GM（1,1）建模的一種方法。本文針對原始序列是凸的情況，首先分析了GM（1,1）模型預測序列的特點，其次提出了改變序列凹凸性的一種新方法，即以原始序列首尾兩點連線為對稱軸，把凸序列轉化為對稱序列（凹序列），再基于對稱序列建立非等間距GM（1,1）模型，從而對原序列進行預測。

1 凹（凸）序列的定義

定義1：設x（0）={x（0）（1），x（0）（2），…，x（0）（n）}為任意一組正序列，對任意k（2≤k≤n-1），若滿足 Δ（0）（k）≤ Δ（0）（k-1），則稱x（0）為凸序列；若滿足 Δ（0）（k）≥ Δ（0）（k-1），則稱x（0）為凹序 列 ，其中 Δ（0）（k）=x（0）（k）-x（0）（k-1）。 特別地 ，當Δ（0）（k）＜ Δ（0）（k-1）時 ，稱x（0）為嚴格凸序列 ；當Δ（0）（k）＞ Δ（0）（k-1），稱x（0）為嚴格凹序列。

定理 1：若序列x（0）={x（0）（1），x（0）（2），…，x（0）（n）} 是凸序列，則滿足不等式：

2x（0）（k）≥x（0）（k+1）+x（0）（k-1）

若x（0）為凹序列，則滿足不等式：

2x（0）（k）≤x（0）（k+1）+x（0）（k-1）

證 明 ：若x（0）是凸序列，則由定義 1 可知 Δ（0）（k）≤Δ（0）（k-1），即：

x（0）（k+1）-x（0）（k）≤x（0）（k）-x（0）（k-1）

從而 2x（0）（k）≥x（0）（k+1）+x（0）（k-1）。同理，可證x（0）為凹序列時，有 2x（0）（k）≤x（0）（k+1）+x（0）（k-1）。

2 原始GM（1,1）模型及其特性

定義 2[1]：設x（0）={x（0）（1），x（0）（2），…，x（0）（n）} 為一非負的原始序列 ，其一次累加序列為x（1）={x（1）（1），x（1）（2），…，x（1）（n）} ，均值序列為Z（1）={z（1）（2），z（1）（3），…，z（1）（n）} ，其中Z（1）（k）=0.5（x（1）（k）+x（1）（k-1））,則稱下列離散等式：

式（1）為灰色GM（1,1）模型的均值形式，稱微分方程。

式（2）為灰色GM（1,1）模型均值形式的白化微分方程。對式（1）由最小二乘法得參數a，b估計值。

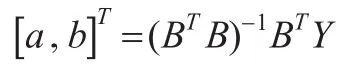
式中：

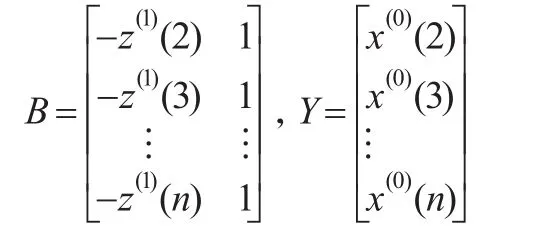
把參數a，b估計值代入式（2）,求得白化方程的解為：

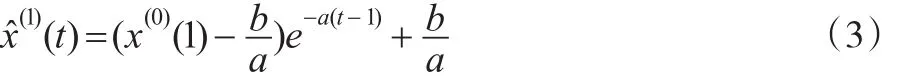
然后離散化,可得時間響應序列：

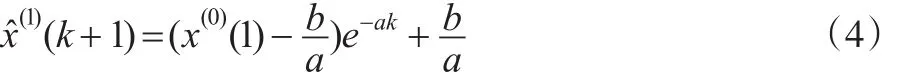
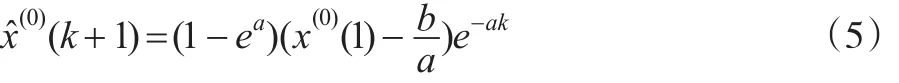
一般來說，GM（1,1）建模序列都是正數序列，如果是負數序列或正負混合序列，則可以通過平移變換轉化為正數序列。因此，在應用GM（1,1）模型進行建模時，其擬合或預測序列也應該是正數序列。下面將論證GM（1,1）模型預測序列的一個顯著特征。

定理2：GM（1,1）模型的擬合預測序列是凹的。

證明：對一切k=1，2，…，不妨假設式（5）都是正數，則有：

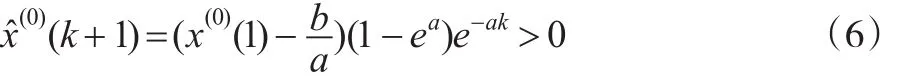
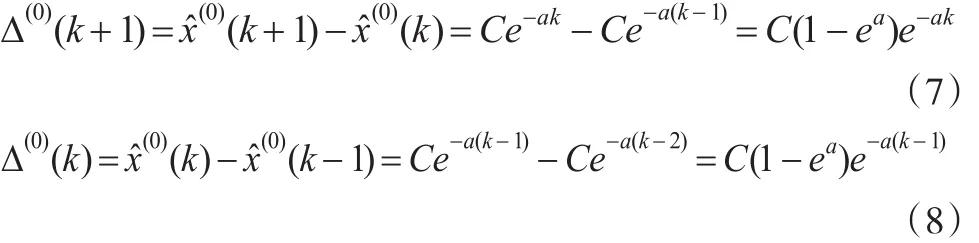
將式（7）與式（8）相比，有：

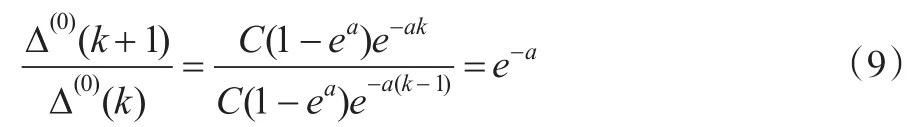
（1）當a＞0時，顯然有e-a＜1，即:

由于 （1-ea）＜ 0 ，于是 Δ（0）（k）=C（1-ea）e-a（k-1）＜ 0 ，代入式（10）則有：

（2）當a＜0時，有e-a＞1，即:

由于 （1-ea）＞ 0 ，于是 Δ（0）（k）=C（1-ea）e-a（k-1）＞ 0 ，代入式（12）則有：

因此，無論原始序列具有什么特征，根據定義1可知GM（1,1）模型的模擬預測序列是凹的。

定理2實際上說明了GM（1,1）模型的擬合預測值是一個凹序列，當原始序列是凸序列時，用式（5）計算得到的GM（1,1）模型擬合序列與原始凸序列的幾何形狀完全相反。因此對原始凸序列直接進行GM（1,1）建模將會產生很大的誤差，預測結果將與原始序列發展態勢不一致。

3 原始凸序列的對稱變換

根據前面對GM（1,1）模型特性分析可知，對原始凸序列進行GM（1,1）建模，會導致很大的模型誤差。如果把凸序列轉換成凹序列就可以避免這種模型誤差。這里選取以第1個點和第n個點的連線作為對稱軸（如圖2所示），進行凹凸性對稱轉換。

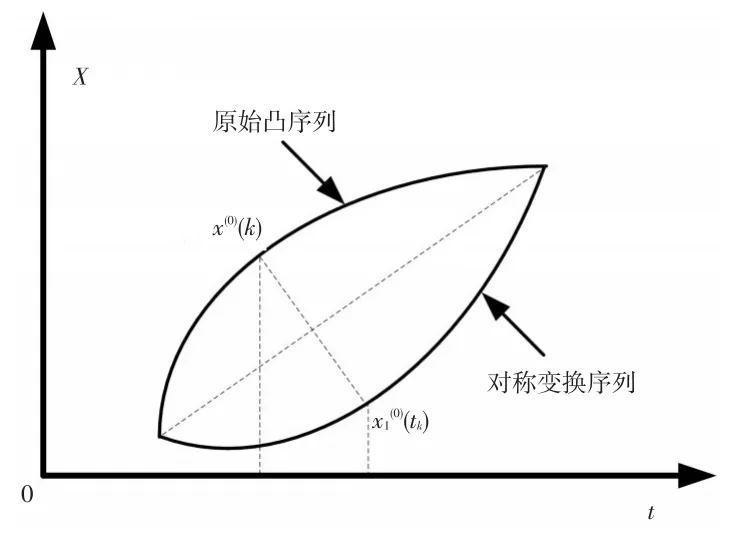
圖1 原始凸序列的對稱變換

定理 3:若X（0）={x（0）（1），x（0）（2），…，x（0）（n）} 為一正的凸序列，其初值化序列為，對進行對稱變換，則得到凹序列，其中:

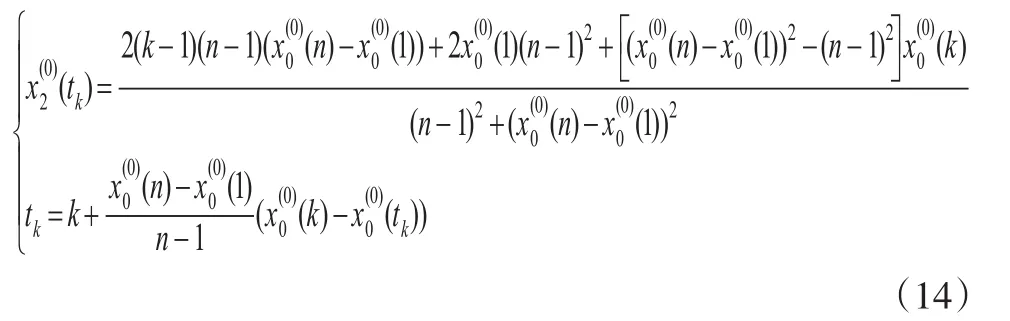
證明：由兩點法，可得到對稱軸的直線方程為:

對于任意一點 （k，（k）），其對稱點為 （tk，（tk）），則兩點中心滿足式（15），即:

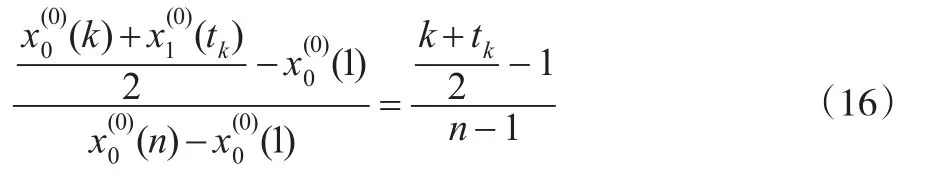
根據兩條垂線斜率乘積為-1，有:

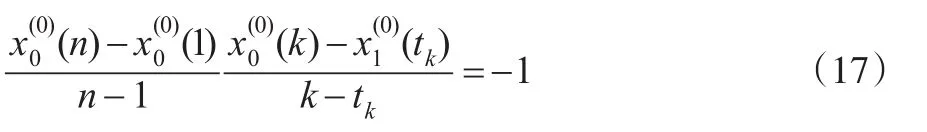
聯立式（16）和式（17），即可解得式（14）。顯然當k=1時，有當k=n時，有

4 基于凸序列對稱變換非等間距GM（1,1）模型

對于原始凸序列經對稱變換之后，由于Δtk（Δtk=tk-tk-1）不為常數，所以對稱變換序列為非等間距序列。這就需要建立非等間距 GM（1,1）模型）+）=b，其與等間距GM（1,1）模型的不同之處在于：

（1）間距序列

Δt={Δt1，Δt2，…，Δtn}，Δt1=1，

Δtk=tk-tk-1，k=2，3，…，n

（2）一次累加序列

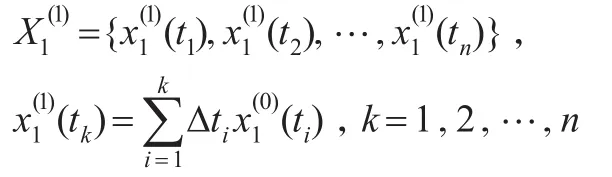
（3）緊鄰均值序列

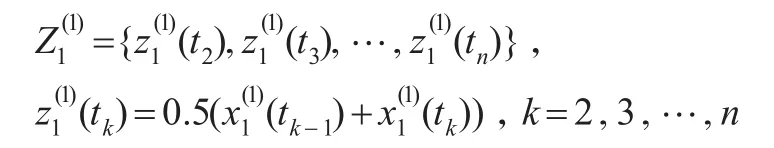
（4）響應函數序列

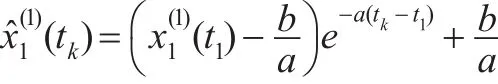
（5）還原值序列

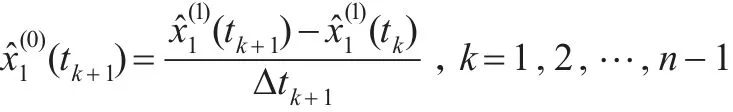
因此，對于凸序列，應用GM（1,1）模型進行預測，首先要對原始序列進行初值化，然后對初值化序列進行對稱變換，基于對稱序列建立GM（1,1）模型，進而由GM（1,1）模型預測對稱序列，最后再逆變換可得原始序列的預測值。具體步驟如下：

第一步：對于一正凸數據序列x（0）={x（0）（1），x（0）（2），…，，先對原始序列初值化變換，得初值化序列；

第三步：基于對稱序列建立非等間距GM（1,1）模型，得擬合序列

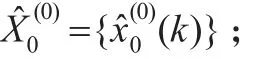
第五步：計算還原值序列

5 實例分析

例1[11]:我國2009—2015年人均天然氣生活消費量為X（0）={13.3，17.0，19.7，21.3，23.8，25.1，26.2} ，單位：立方米。這是個單調遞增具有上凸特征的序列，這里用本文方法對原始數據進行對稱變換再建立GM（1,1）模型，其模擬結果見表1所示。

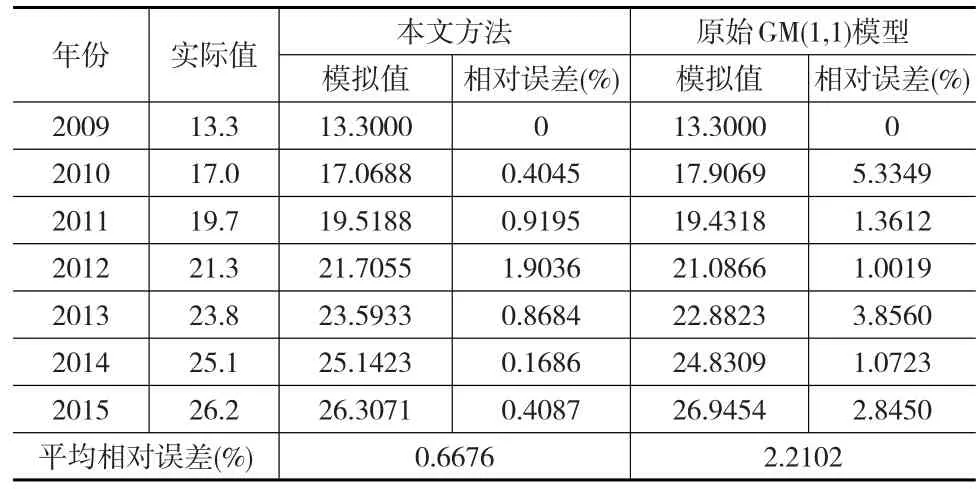
表1 基于GM（1,1）模型2009—2015年我國人均天然氣生活消費量模擬結果

從表1可以看出，本文方法擬合平均相對誤差明顯小于直接GM（1,1）建模的平均相對誤差。因此，對于單調遞增的凸數據序列，需要把凸數據序列轉化為凹數據序列進行GM（1,1）建模，其建模精度更高。

例2：薩莫特洛爾油田是俄羅斯的第一大油田，1969年投產，1980年的產量達到峰值，在1980—1988年遞減階段的年產量分別為：X（0）={15.48，15.03，14.38，14，13.06，12.09，10.98，9.88，8.27}，其單位：107t/年。這顯然是個單調遞減的凸數據序列，如果也用本文中給出方法進行數據對稱變換再建立GM（1,1）模型，模擬結果見表2所示。

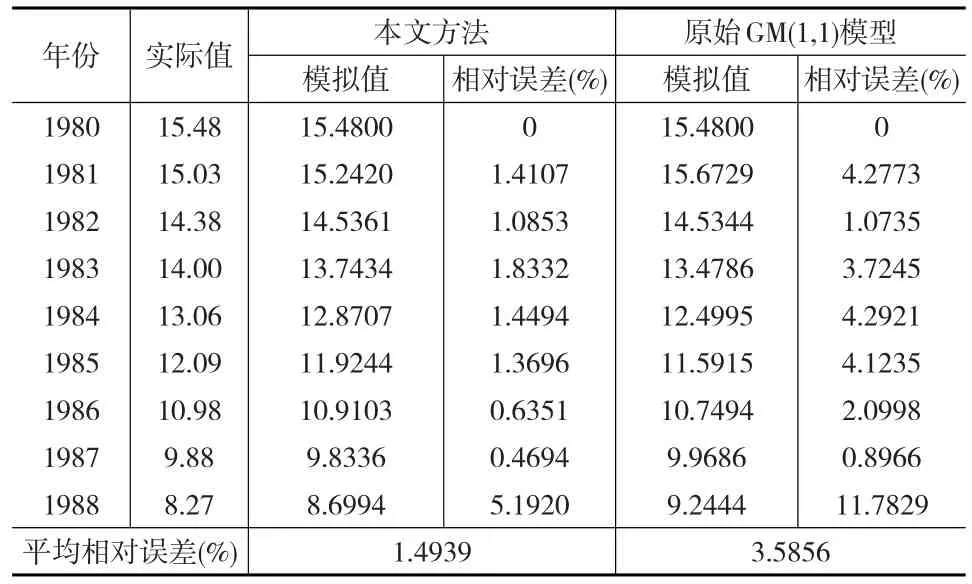
表2 基于GM（1,1）模型薩莫特洛爾油田遞減階段的年產量模擬結果

表2比較結果也顯示：本文方法擬合誤差比直接GM（1,1）建模誤差要小很多。因此，對于單調遞減的凸數據序列，同樣需要對凸數據序列進行凹凸性轉換，才能取得更好的GM（1,1）建模效果。

6 結束語

根據本文證明可知，GM（1,1）模型的模擬預測序列具有凹向性，因此GM（1,1）模型適合凹數據序列建模。對于凸數據序列，要使得預測結果符合原始序列的發展趨勢，需要對原始數據進行對稱變換，否則預測結果失真。經過進一步研究發現，對于凸數據序列采用GM（1,1）模型預測時，僅對GM（1,1）模型參數進行優化，GM（1,1）模型擬合精度并不能有效提高，其預測結果更偏離原始序列發展趨勢。要想從根本上解決模型誤差，可以借助對稱變換，把原始序列是凸的轉換成凹的，然后再進行GM（1,1）建模。