中國制造業(yè)生產(chǎn)率增長研究
王蛟龍,代智慧
(中南財(cái)經(jīng)政法大學(xué) 經(jīng)濟(jì)學(xué)院,武漢 430073)
0 引言
改革開放以來,我國經(jīng)濟(jì)快速增長,制造業(yè)也獲得了發(fā)展良機(jī),取得了長足的進(jìn)步。但是在勞動(dòng)生產(chǎn)率方面,我國同發(fā)達(dá)經(jīng)濟(jì)國家和地區(qū)相比,仍舊有相當(dāng)大差距,這就導(dǎo)致了我國制造業(yè)生產(chǎn)效率不高。因此,研究我國制造業(yè)的生產(chǎn)率增長,對于提升制造業(yè)生產(chǎn)效率,促進(jìn)制造業(yè)發(fā)展有重要意義。
對于我國企業(yè)生產(chǎn)率的研究,學(xué)者們選擇的數(shù)據(jù)和方法存在差異。測算生產(chǎn)率方法主要分為參數(shù)和非參數(shù)兩大類方法。先前的生產(chǎn)率測算主要采用宏觀層面匯總的數(shù)據(jù),其缺陷在于測算結(jié)果的準(zhǔn)確性以及難以反映經(jīng)濟(jì)體結(jié)構(gòu)的動(dòng)態(tài)變化和企業(yè)的異質(zhì)性。與現(xiàn)有研究相比,本文將從以下幾方面進(jìn)行拓展分析:一是本文通過ACF方法進(jìn)行了中國制造業(yè)企業(yè)1999—2016年全要素生產(chǎn)率的測算,目前此方法在國內(nèi)的運(yùn)用還較少,而且是從企業(yè)的層面進(jìn)行測算;二是本文對于全要素生產(chǎn)率研究的兩種主流方法——ACF方法與LP方法做了一個(gè)比較研究,更加直觀地看出ACF方法在對內(nèi)生性的優(yōu)化處理以及計(jì)算結(jié)果方面更加精確;三是本文通過對我國制造業(yè)三類行業(yè)結(jié)構(gòu)的生產(chǎn)率情況加以比較,結(jié)合國家最新產(chǎn)業(yè)政策進(jìn)行分析。
1 研究方法
1.1 LP方法
通常采用Cobb-Douglas生產(chǎn)函數(shù)。本文對于C-D函數(shù)取對數(shù)就可以將其轉(zhuǎn)化為如下線性形式:
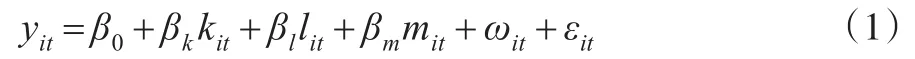
式(1)中,yit為取對數(shù)的企業(yè)的產(chǎn)出增長值;kit為取對數(shù)的資本存量;lit為取對數(shù)的勞動(dòng)力投入量;mit為取對數(shù)的中間投入品使用量;ωit為研究者無法觀測的隨時(shí)間變化的企業(yè)生產(chǎn)率,但是企業(yè)相關(guān)決策者卻可以觀測到;εit為偏離預(yù)設(shè)水平的生產(chǎn)率沖擊及測量被解釋變量產(chǎn)生的誤差。其中,yit、kit、lit這些都能被觀察。而ωit和εit則是兩個(gè)計(jì)量無法觀察項(xiàng)。
LP方法設(shè)定中間投入品使用量mit是關(guān)于生產(chǎn)率ωit和資本存量kit的函數(shù),mit=ft(kit,ωit),在給定kit的條件下,設(shè)定mit是關(guān)于生產(chǎn)率ωit的嚴(yán)格單調(diào)函數(shù),求出ωit關(guān)于mit、kit的反函數(shù),ωit=(kit,mit),代入式(1)中,可以得到:
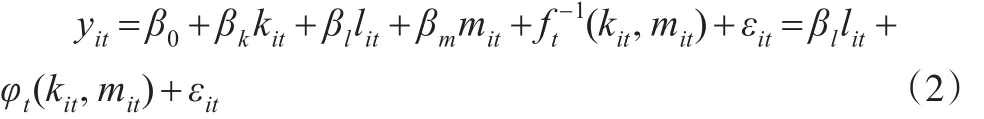
(1)LP方法的第一階段:
本文用資本和中間品使用量的多項(xiàng)式來擬合全要素生產(chǎn)率,來估算相關(guān)系數(shù)。得到LP方法第一階段的廣義矩估計(jì):
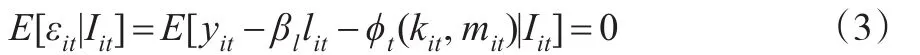
(2)LP方法的第二階段:
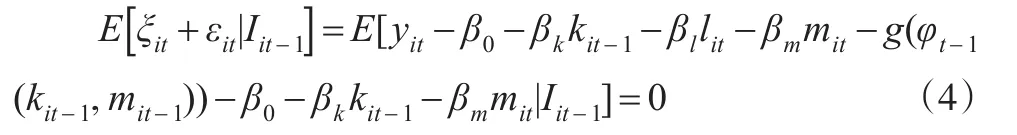
1.2 ACF方法
本文考慮“增長值”生產(chǎn)函數(shù):
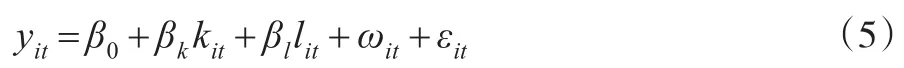
式(5)中,yit為取對數(shù)的企業(yè)的增長值(注:這里同OP方法一樣,是企業(yè)的增長值);kit為取對數(shù)的資本存量;lit為取對數(shù)的勞動(dòng)力投入量;ωit為企業(yè)的異質(zhì)性生產(chǎn)率,隨時(shí)間變化;εit為偏離預(yù)設(shè)水平的生產(chǎn)率沖擊及測量被解釋變量產(chǎn)生的誤差。
ACF方法提出一種新的數(shù)據(jù)生成機(jī)制(GPD):
公司積累資本根據(jù)下式確定:
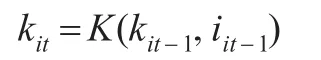
這里,投資iit-1在時(shí)期t-1被選擇,決定的指標(biāo)為kit。勞動(dòng)投入lit有潛在的動(dòng)態(tài)隱含意義,在時(shí)期t-b被選擇(0<b<1)。在時(shí)期t,決定的指標(biāo)為mit。
中間投入品如下定義:
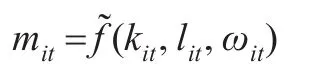
給定這些假設(shè),可以求出ωit的反函數(shù)表達(dá),并代入到生產(chǎn)函數(shù),式(1)中可以得到:
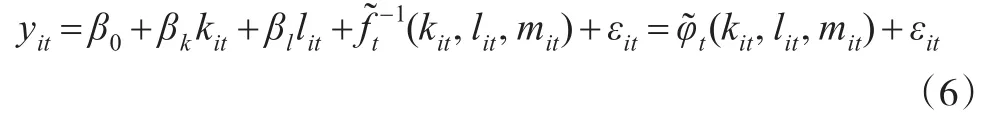
(1)ACF方法的第一階段
對式(6)采取多項(xiàng)式的擬合,并用OLS方法進(jìn)行回歸,可以得到的估計(jì)值。這完成了ACF估計(jì)的第一階段。具體為用kit、lit、mit的二次多項(xiàng)式(包括水平值、二次項(xiàng)以及交叉項(xiàng))來表示(kit,lit,mit)。代入式(6)中,用實(shí)際的數(shù)據(jù)做OLS回歸,得到二次多項(xiàng)式的具體表達(dá)式,即估計(jì)值。于是可以得到εit的表達(dá)式:

(2)ACF方法的第二階段
矩條件一:
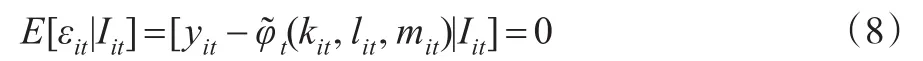
這里設(shè)定生產(chǎn)率變動(dòng)遵從馬爾科夫的一階過程,ωt=E[ωt|ωt-1]+ξt,ξt是生產(chǎn)率沖擊且與資本kit不相關(guān)。
考察ωit的時(shí)期t-1條件期望,可以得到:
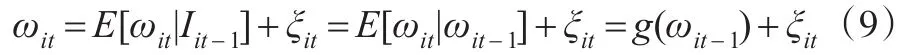
矩條件二:

矩條件三:
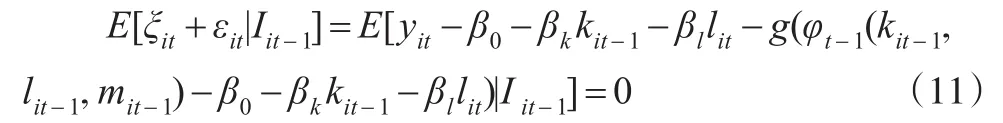
條件四(非條件矩):
相比較于LP方法,ACF方法在第二階段需要估計(jì)一個(gè)額外參數(shù)βl,于是ACF方法需要一個(gè)額外的非條件矩。為了說明,本文定義ωit:
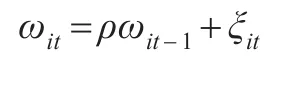
將ωit的表達(dá)式代入式(11),并用多項(xiàng)式乘積形式表達(dá)矩陣的方法,于是得到:
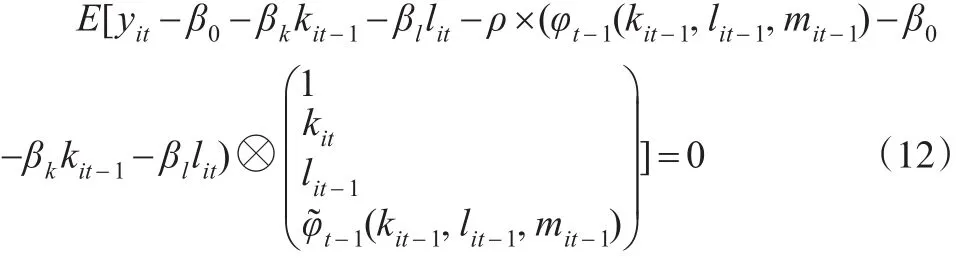
由上述4個(gè)條件,算出4個(gè)值β0、βk、βl和ρ。
最后,計(jì)算出ωit=?(kit,lit,mit)-(β0+βkkit+βllit)。
2 變量選擇與數(shù)據(jù)處理
本文測算我國制造業(yè)企業(yè)1999—2016年全要素生產(chǎn)率,使用了ACF方法和LP方法,基礎(chǔ)數(shù)據(jù)來自我國1998—2016年《中國統(tǒng)計(jì)年鑒》《中國工業(yè)經(jīng)濟(jì)統(tǒng)計(jì)年鑒》以及出自國家統(tǒng)計(jì)局的《中國工業(yè)企業(yè)數(shù)據(jù)庫》。由于LP、ACF方法的測算過程中,在計(jì)算當(dāng)期的企業(yè)生產(chǎn)率的過程中,需要用到前一期同一家企業(yè)的信息集。因此需要采集1998—2016年相關(guān)數(shù)據(jù),1998年的企業(yè)數(shù)據(jù)作為第一期數(shù)據(jù),供1999年企業(yè)測算生產(chǎn)率使用,即具體的測算研究是從1999年開始的。
盡管中國工業(yè)企業(yè)數(shù)據(jù)庫比較詳實(shí),但其中也存在記錄有誤的樣本和空缺項(xiàng)[1]。參照謝千里等(2008)[2]、楊汝岱(2015)[3]并結(jié)合實(shí)際變量的需要,本文選取了制造業(yè)企業(yè),并對數(shù)據(jù)做了相應(yīng)篩選:一是刪除了變量有所遺漏的樣本,比如剔除工業(yè)增加值、工業(yè)總產(chǎn)值、工業(yè)銷售額小于或等于0的樣本;二是提取了從業(yè)企業(yè)職工人數(shù)大于或等于8的樣本;三是剔除生產(chǎn)率過大和過小的企業(yè)樣本。
經(jīng)過處理后的數(shù)據(jù)中,1998—2016年的企業(yè)樣本一共5171610家企業(yè),其中相鄰兩年能夠匹配上,適用于計(jì)算全要素生產(chǎn)率的企業(yè)樣本一共3631089家企業(yè)。
本文測算過程中采用企業(yè)工業(yè)增加值作為產(chǎn)出量,中間投入品是包括原材料、電、石油等的加總值。同時(shí)做了價(jià)格指數(shù)平減處理,用各變量數(shù)據(jù)除以對應(yīng)價(jià)格平減指數(shù),從而得到實(shí)際值,從中經(jīng)網(wǎng)統(tǒng)計(jì)數(shù)據(jù)庫中得到價(jià)格平減指數(shù)表(以1995年為第一期)。計(jì)算折舊時(shí)使用永續(xù)盤存法,用實(shí)際投資值做為投資量計(jì)算。勞動(dòng)變量指標(biāo)采用企業(yè)從業(yè)人數(shù)。
3 實(shí)證分析
3.1 全要素生產(chǎn)率測算結(jié)果
本文采用ACF與LP方法對我國制造業(yè)企業(yè)1998—2016年企業(yè)數(shù)據(jù)進(jìn)行測算,使用軟件版本為Stata12.0,用Stata軟件包levpet來測算,得出了1999—2016年我國制造業(yè)企業(yè)TFP,再采用各企業(yè)的工業(yè)增加值為權(quán)重,從行業(yè)層面來研究計(jì)算生產(chǎn)率。具體結(jié)果如下頁表1所示。
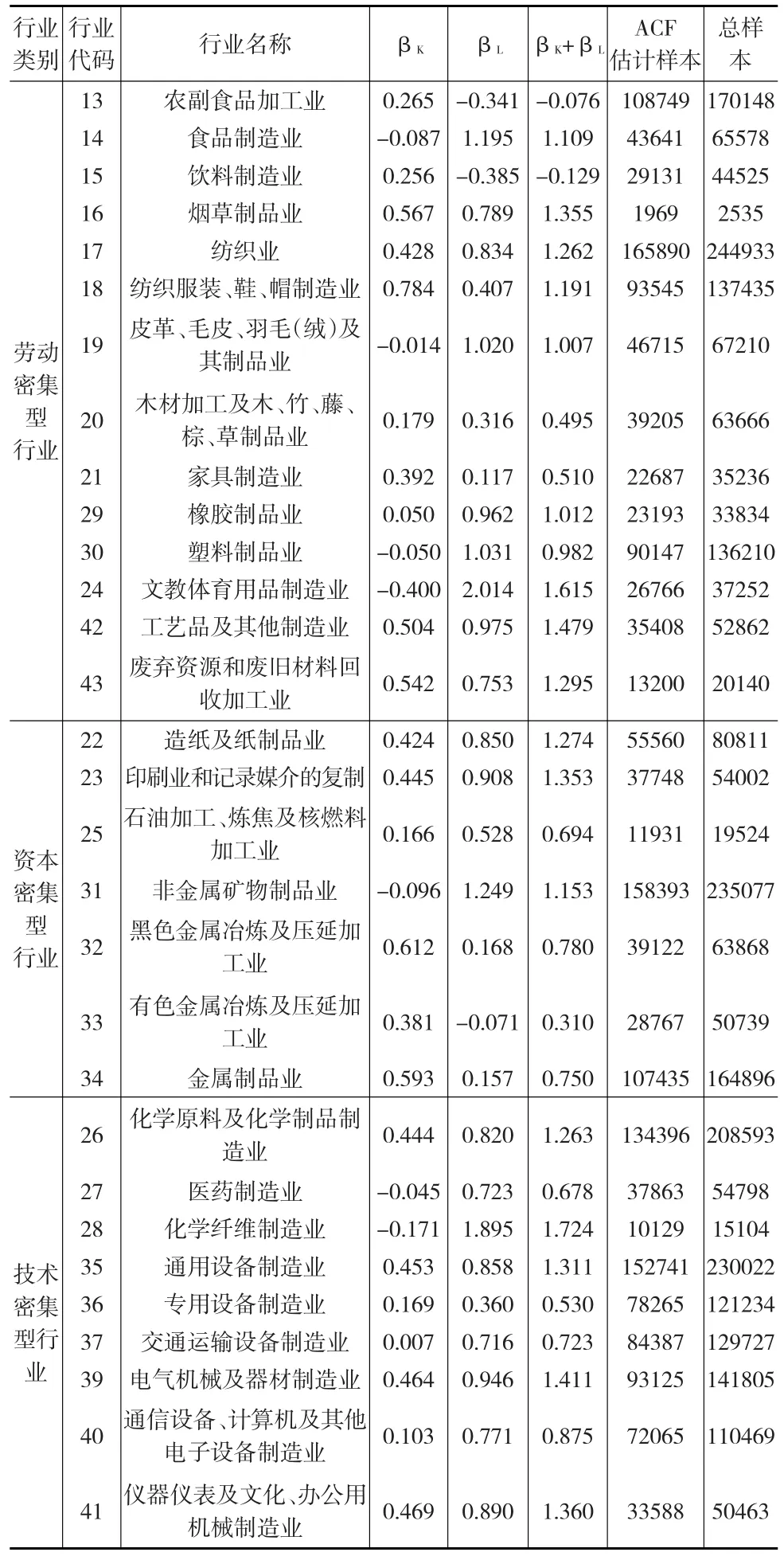
表1 我國制造業(yè)分行業(yè)資本、勞動(dòng)系數(shù)彈性(ACF方法測算結(jié)果)
3.2 生產(chǎn)率的行業(yè)比較分析
相同測算研究和相關(guān)檢測后,本文發(fā)現(xiàn)ACF方法在內(nèi)生性問題上更有優(yōu)越性,獲得了相對較好的估算結(jié)果,本文中主要用ACF方法測算的TFP結(jié)果作為分析的依據(jù)。通過兩種方法的比較,ACF方法在解決內(nèi)生性上有以下幾個(gè)方面的優(yōu)越性:一是,ACF方法具體的參數(shù)估計(jì)從第二階段才開始,無論是模型還是測算更為簡潔;二是,ACF方法同LP方法都是半?yún)?shù)的方法,在實(shí)際運(yùn)用過程中適用范圍更廣泛;三是,ACF方法在第二階段運(yùn)算過程中巧妙地運(yùn)用了相同矩條件的轉(zhuǎn)換運(yùn)算,對參數(shù)進(jìn)行估計(jì),有效克服內(nèi)生性。
本文估算出的我國制造業(yè)TFP的各年均值為3.04,與魯曉東和連玉君(2012)[4]、楊汝岱(2015)[3]等的結(jié)果大致相符。從TFP年均速度來看,我國制造業(yè)TFP1999—2016年均增長速度為7.27%,這也與邵軍等(2011)[5]、余淼杰等(2015)[6]利用宏觀和行業(yè)數(shù)據(jù),估算出90年代以來TFP年均增長約為5%的結(jié)果大致相符。但由于各學(xué)者采用的年份數(shù)據(jù)不同,估算方法不同,得出的我國TFP年均增長速度有所差異,但大多數(shù)文獻(xiàn)發(fā)現(xiàn)我國TFP年均增長速度在3%~6%之間,本文得出的TFP年均7.27%的增長速度略高于此范圍。
從勞動(dòng)密集型行業(yè)、技術(shù)密集型行業(yè)、資本密集型行業(yè)的TFP年均增長速度分別為7.18%、6.91%、7.70%。可以得出:技術(shù)密集型行業(yè)的TFP年均增長速度最低;與之比較,勞動(dòng)密集型行業(yè)、資本密集型行業(yè)的TFP年均增長速度反而高些。
我國制造業(yè)分行業(yè)中生產(chǎn)率增長最快的是黑色金屬冶煉及壓延加工業(yè)、石油加工、煉焦及核燃料加工業(yè)、電氣機(jī)械及器材制造業(yè),可以看出這幾個(gè)行業(yè)都屬于高新技術(shù)相關(guān)行業(yè),生產(chǎn)率增長迅速。
4 結(jié)論
本文基于1998—2016年我國制造業(yè)行業(yè)的面板數(shù)據(jù),采用ACF方法和LP方法,先后測算出我國制造業(yè)企業(yè)層面全要素生產(chǎn)率,進(jìn)行分行業(yè)資本、勞動(dòng)系數(shù)彈性分析等,得到以下結(jié)論:
第一,從整體看,我國制造業(yè)的整體生產(chǎn)率在1999—2016年是穩(wěn)步增長的。其中1999—2001年增長格外迅猛,規(guī)模以上企業(yè)數(shù)也逐步增長。這也反映出這段時(shí)期制造業(yè)發(fā)展環(huán)境良好,很大程度上得益于國家行業(yè)政策宏觀調(diào)控。
第二,亟需提高我國技術(shù)密集型行業(yè)的技術(shù)集中度,提倡科技創(chuàng)新,推動(dòng)技術(shù)進(jìn)步。技術(shù)密集型行業(yè)的技術(shù)創(chuàng)新、技術(shù)使用度需要進(jìn)一步提高,很多分類上是“技術(shù)密集型”的企業(yè),例如電子計(jì)算機(jī)的制造企業(yè)等,其中核心的技術(shù)如電腦芯片的制造,都來源于國外。技術(shù)度不高的資本密集型行業(yè)、勞動(dòng)密集型行業(yè)的生產(chǎn)率卻一直在穩(wěn)步增長。勞動(dòng)密集型行業(yè)如紡織業(yè)等,吸納了社會(huì)相當(dāng)多的勞動(dòng)力,對于維持國民經(jīng)濟(jì)正常運(yùn)行,解決就業(yè)問題有著特殊的作用,依舊需要鼓勵(lì)和推動(dòng)該行業(yè)持續(xù)進(jìn)步,實(shí)現(xiàn)合理與優(yōu)化發(fā)展。
第三,高新技術(shù)行業(yè)是生產(chǎn)率增長最快的行業(yè),相關(guān)的行業(yè)扶持政策效果較為顯著。傳統(tǒng)行業(yè)的生產(chǎn)率增長較慢,如文教體育用品制造業(yè)、家具制造業(yè)、服裝等,推行傳統(tǒng)行業(yè)技術(shù)革新任重道遠(yuǎn),需要有新的產(chǎn)業(yè)政策來積極引導(dǎo),實(shí)現(xiàn)穩(wěn)定持續(xù)發(fā)展。

