GPRs搭接網絡分解優化定理在流水作業中的應用

孔 峰，張 睿，吳 甜

(華北電力大學經濟與管理學院，河北 保定 071003)

1 引言

GPRs(Generalized Precedence Relations)搭接網絡計劃技術是在經典的CPM網絡計劃技術基礎上的發展[1]，由Crandall[1]在1973年提出后廣泛吸引了各國學者和應用者的注意。在GPRs網絡計劃中相鄰工序之間的時間約束(搭接)關系，不僅存在傳統的FTS(Finish To Start)型的，還存在FTF(Finish To Finish)、STS(Start To Start)、STF(Start To Finish)型時間約束。這種帶有多種時間約束關系的網絡計劃更貼合工程實際，尤其在工期長、工序多、工藝復雜的大型工程項目中具有廣闊的應用前景。

當前，關于GPRs網絡計劃悖論和最短工期研究也日益廣泛。Elmaghraby和Kamburowski[2]對GPRs網絡的基本概念做出了系統地闡述，奠定了GPRs網絡的理論基礎，并發現其中存在逆向關鍵工序引起的總工期悖論。劉樹良等[3]提出搭接網絡中存在某些關鍵工序在壓縮量較大時，總工期不但縮短反而延長，以及壓縮或延誤關鍵工序總工期均不變的奇異現象等等。闞芝南等[4]發現雙代號搭接網絡中存在“工序間加入不同表現形式的同一時間約束，可能會產生不同的最大路長”這個悖論，并提出雙代號搭接網絡的一種新表示方法和求解搭接網絡次關鍵路線的一系列精確算法。蘇志雄等[5]設計了新的表示方法，即將工序之間所有的搭接關系都等效的利用傳統的CPM法表示，在新的表示方法中發現了某些關鍵工序的縮短，總工期反而延長，而某些非關鍵工序無論如何變動，其總時差總保持不變等現象。這些研究為項目計劃優化問題提出了新的挑戰，開拓了GPRs搭接網絡在研究和應用上的新領域。

國內學者將重復性項目調度稱為“流水施工”或“流水作業”[6]，基于GPRs網絡的重復性建設項目工期計劃的研究具有重大的實際意義。關鍵路線的長度決定項目總工期，研究認為流水作業中施工段的劃分對關鍵線路的長度有重要影響，科學合理的劃分施工段會大大縮短關鍵線路長度。其中具有代表性的研究有：Selinger[7]最早提出了重復性項目中的最短工期問題，其假定所有工序均存在多種可選擇執行模式，并在保持工作連續性要求和資源恒定性要求條件下給出了該問題的動態規劃求解模型。Harris和Ioannou[8]在重復性工程項目進度計劃管理中也引入了GPRs網絡，發現總工期悖論也會出現。重復性建設項目需要合理計劃，以確保資源的不間斷使用，Harris和Ioannou[8]認為傳統關鍵路徑法不能滿足此要求，提出采用重復調度方法(RSM)以保證施工計劃中的資源連續性。Alexandros等[9]比較了Kallantzis -Lambropoulos的關鍵路徑重復項目模型與網絡計劃關鍵路徑法，指出了兩者之間的異同。楊冰[10-11]把網絡計劃、搭接網絡計劃和流水網絡計劃統一起來，計算模型更為嚴謹、簡明、便于應用。蔣根謀[12]等稱流水作業計劃為線性計劃方法，并介紹了線性進度計劃的繪制方法和步驟。張立輝等[13]提出了借助約束線確定重復性項目中關鍵路線的方法。總之基于GPRs網絡的工期優化方法已經成為流水作業研究的主流方向之一。

通過對GPRs網絡的總工期悖論研究，本文首次發現了在GPRs搭接網絡中還存在“分解悖論”，即編制網絡計劃時，將某一個可分解的關鍵工序分解成兩個順序工序(FTS=0)以后，總工期并非保持不變反而縮短的奇異現象，工序的分解也使工序獲得更多可利用的總時差。通過對該分解悖論的研究，本文提出了兩個分解優化定理，用于GPRs搭接網絡計劃的優化。這種優化方法不僅解決了GPRs搭接網絡中正確求解最短總工期的問題，還發現在總工期不變的條件下，分解某一非關鍵工序會增加其總時差。總時差的增加為資源優化創造了條件。工序的合理分解(施工段的科學劃分)正是流水作業的重要內容之一，本文將該分解優化方法同流水作業原理相結合，用于解決流水作業中施工段劃分的問題，并通過實例驗證了該方法的可操作性。這對大型重復性項目的建設有著重要的實踐指導意義。

2 GPRs搭接網絡的關鍵工序分解悖論

在實際施工過程中，大部分工序因為技術間歇、人員調度、機械設備調度、工作時間限制等各種各樣的原因，可以進行合理分解，尤其是對于大型重復性項目。傳統CPM理論認為關鍵工序被分解成若干具有FTS=0的工序，總工期和時間參數均不會發生改變；在某工序中插入一段休息時間會使項目的總工期變長。但本文研究發現對特定工序進行分解，反而使總工期減少，工序的機動時間也得到增加。這種不需要增加資源投入量的工序分解方式，不但滿足工期優化的目標，還節省了大量的資金成本。

本文以如圖1所示的網絡圖為例進行分析。

圖1 GPRs搭接網絡計劃圖初始方案

2.1 分解悖論現象

在搭接網絡計劃中，工序間的約束關系是由相鄰兩工作之間的施工速度決定的。如果前一工序施工速度較后一工序快，則采用“STS”型；如果前一工序施工速度比后一工序慢，則采用“FTF”型。圖1的搭接網絡中各個字母表示不同工序，其中St表示開始工序，Fin表示結束工序，僅表示邏輯關系不具有實際意義。

圖1網絡圖中關鍵線路為St→A→E→F→ H→Fin,總工期為46，工序A、E、F、H為關鍵工序。將工序E分解為E1和E2兩個具有FTS=0的順序工序，工序持續時間分別為3和4，重新繪制和計算網絡圖，結果如圖2所示。

根據圖2的計算結果可以看出，工序分解后關鍵線路發生了變化，為St→C→D→G→Fin,而且E1和E2都不再是關鍵工序，總工期也縮短為41。顯然，當關鍵工序E可以分解時，分解之后的網絡圖優于初始網絡圖。

分解悖論還可以用另一種表現形式——咖啡時間悖論來說明。

在初始網絡圖中的關鍵工序E中插入1個咖啡時間(休息時間)E0，即在拆分后的工序E1和E2中，插入一個持續時間很短的工序E0，則E1、E0和E2成為三個搭接關系為FTS=0的順序工序，持續時間分別為3、1、4，重新計算網絡圖后結果如圖3所示。

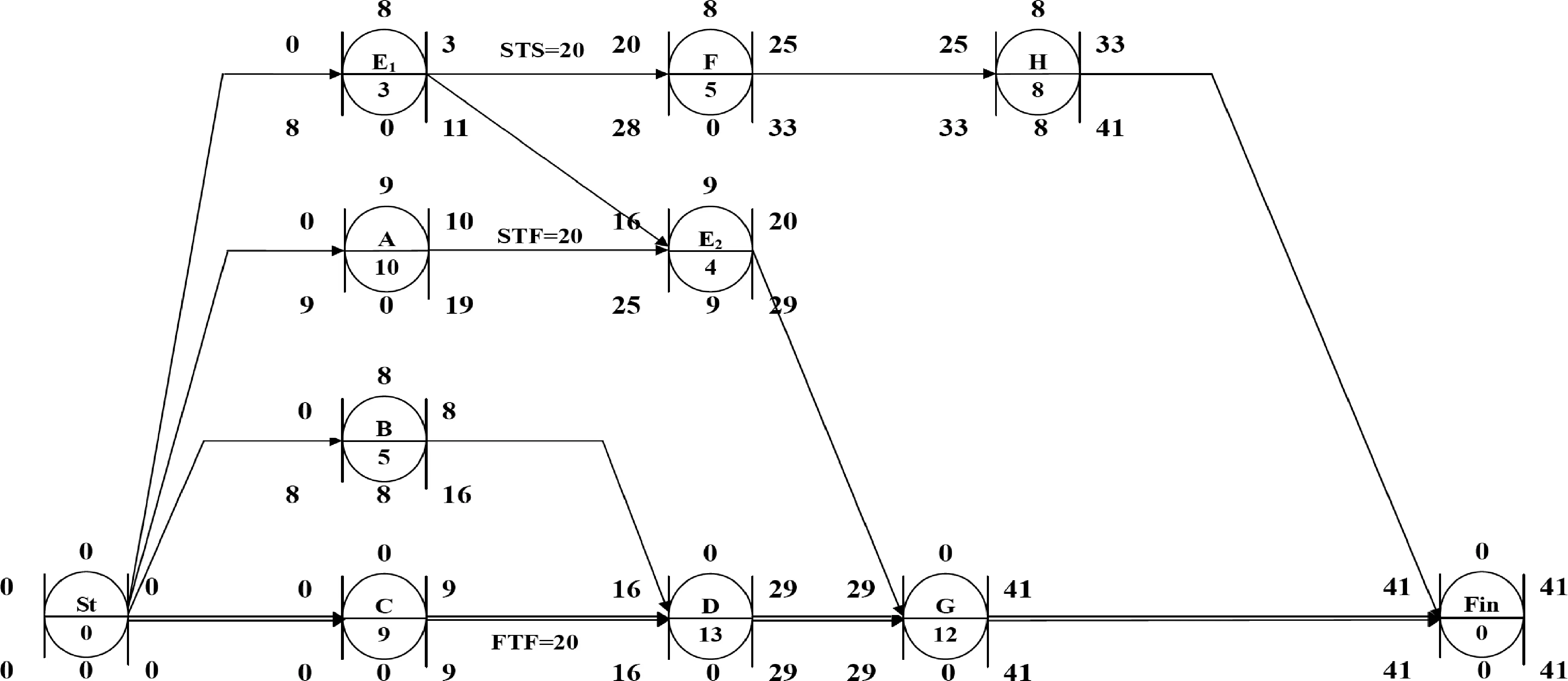
圖2 關鍵工序分解悖論

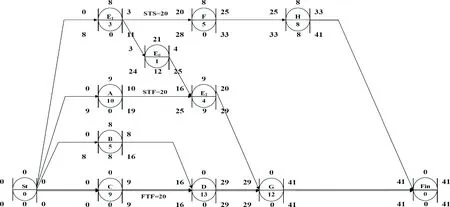
圖3 咖啡時間悖論

相比于初始網絡圖，增加工序后總工期反而減少為41天，關鍵線路變為St→C→D→G→Fin。這種在某一可分解關鍵工序中插入休息時間(咖啡時間)后，工序雖然增加了，但是總工期卻縮短的現象稱為咖啡時間悖論。圖3的原理與圖2相同。

2.2 悖論原因分析

(1)關于關鍵工序分解悖論的分析

將某關鍵工序進行合理分解，總工期縮短的原因在于：由于工序A、E之間為STF的搭接關系，即工序A只對E的結束有直接約束，分解后該約束變為A與E2之間，工序E2需要在工序A開始后20內結束。工序E1與工序A沒有直接約束關系。因此，項目開始后E1即可開始，E1最早開始時間提前了13。又由于工序E1和F之間為STS搭接關系，這就使得工序F的最早開始時間也提前了13，其所在線路長度縮短，使得關鍵線路發生變化，總工期縮短。

(2)關于咖啡時間悖論的分析

咖啡時間悖論和分解悖論產生的原因相似，插入咖啡時間后工序A僅對工序E2有STF的搭接關系，工序E1與工序A并不存在直接約束，所以E1工序的最早開始時間也提前，由于工序E1和F之間為STS搭接關系，這就使得工序F的最早開始時間也提前了，線路長度縮短，導致關鍵線路發生變化，總工期縮短。

2.3 關鍵工序分解優化定理

分解悖論(包括咖啡時間悖論)的存在，說明在項目沒有增加資源投入的情況下，甚至增加休息時間，總工期卻縮短。也就是說，原有網絡計劃中存在帕累托改進。因此，需要進行更科學的優化，在不增加資源投入的條件下，確保實現最優(最短)總工期。GPRs網絡中存在如下的關鍵工序分解優化定理。

分解優化定理1：

若某一網絡圖中所有的關鍵線路，均存在如下情況，網絡的總工期是可以得到優化的。

(1)某些關鍵工序是可以進行分解的；

(2)該關鍵工序與其緊前關鍵工序之間存在STF或FTF的搭接關系，且該關鍵工序與其緊后關鍵工序之間存在STS或STF的搭接關系。

證明：

只需證明其中1條關鍵路線的長度可以縮短，其它關鍵線路同理即可。

(1)在某關鍵路線中，某關鍵工序j與其緊前工序i之間存在STF的搭接關系，與其緊后工序k存在STS的搭接關系(簡稱STF-STS組合)。ESk為工序k的最早開始時間，STSj-k表示工序j與k之間存在STS的搭接關系，其他類似。

分解前，有，ESk=ESj+STSj-k

由于工序j為關鍵工序，其最早完成時間由與其具有STF搭接關系的緊前關鍵工序i決定，因此有，

ESj=max(EFj-tj,其它約束)=EFj-tj

即有，EFj-tj>其它約束。

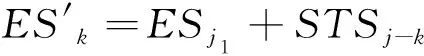
由于工序j1與工序i之間沒有了約束，其最早時間由其它約束決定，即，ESj1=max(其它約束)

所以有，ESj>ESj1。

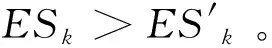
所以經過工序k的關鍵線路變短。

(2)其它三種情況類似，即STF-STF組合、FTF-STS組合、FTF-STF組合證明同上，略。

證畢。

3 總時差悖論及搭接網絡分解優化方法

3.1 總時差悖論現象

分解悖論不僅僅體現在關鍵工序和總工期的改變上，進一步分析，經觀察可發現，圖3中插入“咖啡時間”E0后，E0總時差為21，證明其有充分的可利用機動時間(總時差)，而且工序E1同E2的總時差并未改變，仍與圖2中相同，分別為8和9。

相比于圖1中沒有總時差的工序E，其可利用的機動時間(總時差)增加了許多。工序總時差的增加，使得項目有更多可利用的機動時間，資源優化空間大幅提升。

工序分解后總時差增加的原因分析：

(1)插入E0前：由于圖2中工序E1和工序F之間STS搭接關系的存在，工序E1的最遲開始時間為LSE1=min(28-20，25-3)=8，是由STS搭接關系決定的。因此，無論E1持續時間如何變化，其總時差為定值8。

而工序A與E2之間STF搭接關系確定了E2的最早完成時間，為固定值20。同時，關鍵線路已確定總工期，所以工序E2的最遲完成時間為29始終不變。因此，工序E2的總時差為定值9。

(2)插入E0后：插入咖啡時間E0后，由于LSE0=min(28-20，24-3)=10，所以E1總時差保持不變為8。且工序E2的總時差仍為定值9天，工序E0具有總時差21，所以插入E0后總時差增加。

該特性不僅存在于非關鍵工序上，同樣也會出現在關鍵工序中。將圖3中的關鍵工序D拆分為D1和D2兩個具有FTS=0搭接關系的順序工序，持續時間分別為10和3，重新繪制并計算網絡圖，如圖4所示。

由圖中計算結果可知，工序D1總時差為8。

圖3和圖4的計算結果證明了有的工序在分解后不僅不會改變總工期，反而為工序自身獲得了更多的總時差。進一步說明合理的分解工序可以達到項目的優化。

3.2 總時差分解優化定理

GPRs中存在如下關于總時差的分解優化定理。

分解優化定理2：

在GPRs網絡中，若存在以下情況，通過工序的分解可以得到更多的總時差，即總時差的分布得到優化。

(1)某工序是可以進行分解的；

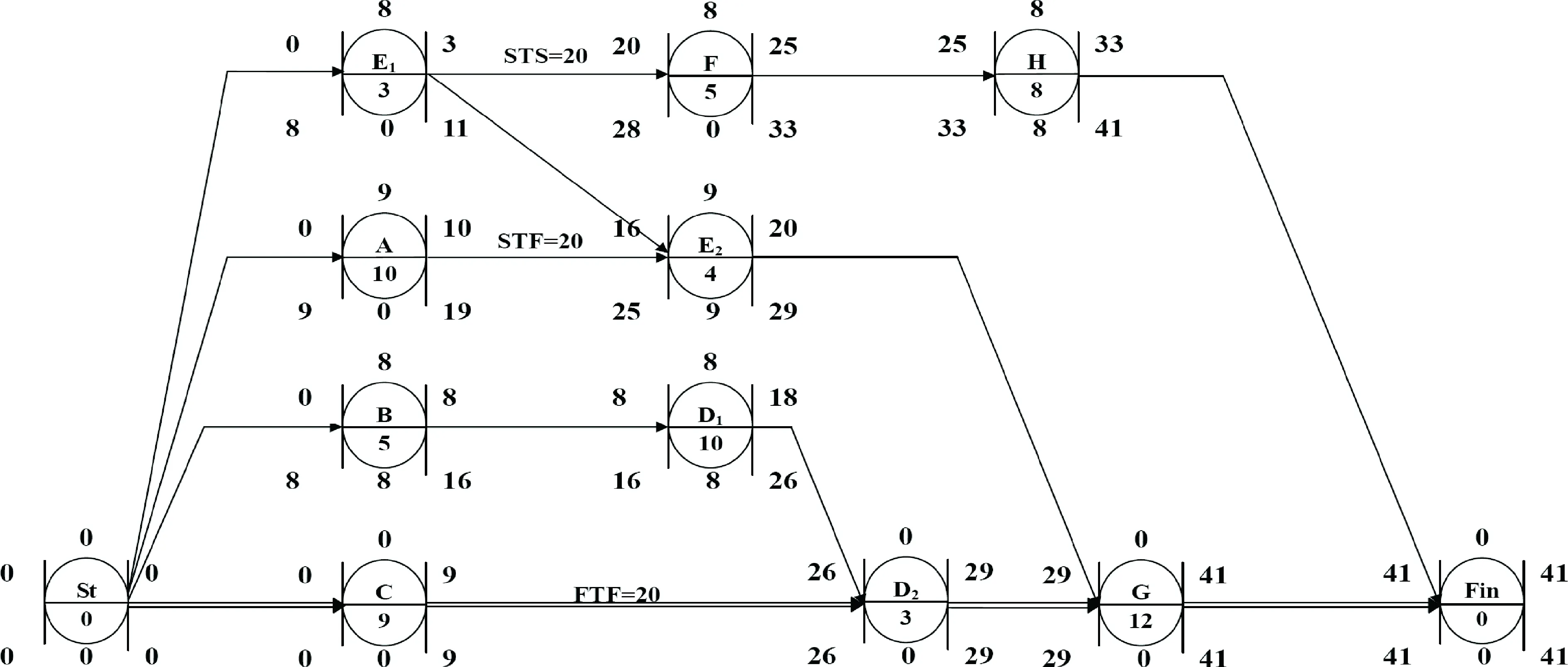
圖4 分解悖論拓展分析——總時差悖論

(2)該工序與其緊前工序之間存在STF或FTF的搭接關系，且該搭接關系是起決定作用的約束；或該工序與其緊后工序之間存在STS或STF的搭接關系，且該搭接關系是起決定作用的約束。

證明：

(1)假設在網絡圖中，某工序i與其緊后工序j之間存在STF的搭接關系，且該搭接關系是起決定作用的約束。

則工序i的最遲完成時間：

LFi=min(EFj-STFij+ti,其它約束)=EFj-STFij+ti

即有，EFj-STFij+tB<其它約束。

工序i分解為工序i1和工序i2后，工序i2的最遲完成時間：

LFi2=min(其它約束)

因此，有，LFi2>LFi。

由于，LFi=LFi-EFi,LFi2=LFi2-EFi2

又因為，

EFi2=ESi2+ti2=EFi1+ti2=ESi1+ti1+ti2

=ESi1+ti=ESi+ti=EFi

因此，TFi2>TFi。

又因為，LSi1=LSi,ESi1=ESi，

因此，TFi1=TFi。

工序i分解后的工序i1的總時差與分解前相同，而工序i2總時差大于i的總時差，說明工序i分解后總時差增加。

(2)其它情況類似，證明略。

證畢。

可以看出，上述兩個分解優化定理本質是相同的，都是通過工序的分解得出工序的最大總時差。可分解的工序與其緊前或緊后工序之間存在搭接關系，約束了其開始或結束時間，通過合理的工序分解使得被約束對象趨于合理。定理1可以得到正確的關鍵工序，定理2可以得到最大的總時差。

3.3 搭接網絡的分解優化方法

根據前面兩個分解優化定理，得到GPRs網絡的分解優化方法：

若某工序可以進行分解，且存在下述起決定作用的搭接關系時，可以按照以下方法進行分解優化：

(1)某工序與其緊前工序若存在STF或FTF的搭接關系，則該工序應該分解為兩個具有搭接關系FTS=0的工序，其中后者為不能繼續分解的基本工序。

(2)某工序與其緊后工序若存在STS或STF的搭接關系，則該工序應該分解為兩個具有搭接關系FTS=0的工序，其中前者為不能繼續分解的基本工序。

因此，對于圖1網絡，最終的優化結果如圖5所示。其中，工序A1、E0、E2、D2為不能分解的基本工序。

相比于圖1 中的初始方案，圖5的方案總工期得到了減少，部分工序的機動時間也大大增加，有的工序還具備了休息緩沖的時間。可見，分解優化定理對于項目優化管理有重要意義。

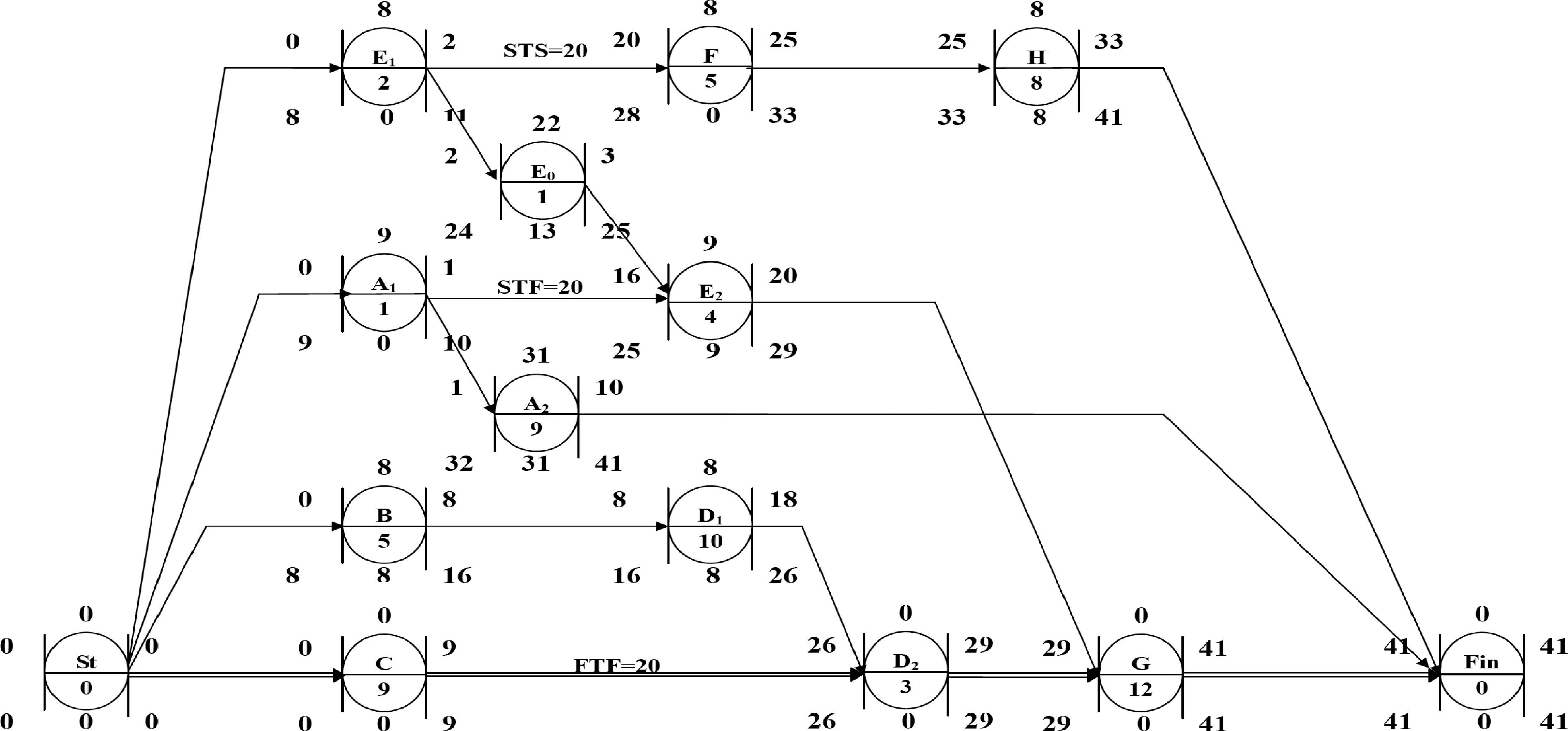
圖5 GPRs搭接網絡圖最終優化方案

4 分解優化定理在流水作業網絡計劃中的應用

流水施工需將擬建工程的全部建造過程根據工藝和工程量分解為若干個施工過程，豎向的劃分稱之為施工層，平面上的劃分稱之為施工段。各組專業工人則根據施工對象的需要劃分成若干個專業小組或混合專業小組，將其按照施工順序安排在工作性質相同施工段上，依次投入施工。流水作業作為一種先進的作業方式得到了廣泛的應用。

施工段的劃分是流水作業施工中最主要的內容之一，將分解優化定理科學合理的應用于流水作業原理中，即通過合理的施工段劃分(工序分解)，會有效的縮短總工期，使得工程項目建設更加高效合理。

本文以下一算例進行分析。

某一高架橋工程，該高架橋全長1189米，基本施工工序包括基礎施工、橋臺施工、橋臺后填土、預制梁的架設、橋面附屬工程和同兩側道路路基的連接。具體施工工序及各工序持續時間如表1所示。為保證工程的早日完工，該工程采用流水作業施工，將基礎、橋臺工程均分為東、西兩個施工段。為盡早通車，加之山溝的地勢條件，該高架橋西側基礎與西側橋臺施工之間存在STS=15天的搭接關系，東側基礎同東側橋臺施工之間存在FTF=20天的搭接關系。此外，架梁時不僅需滿足橋梁自身的使用要求，也要保證同兩側公路路基對接良好，故架梁工序同橋面系及附屬工程之間存在STF=20天的搭接關系，STSC-D表示工序C與D之間存在開始到開始的搭接關系。

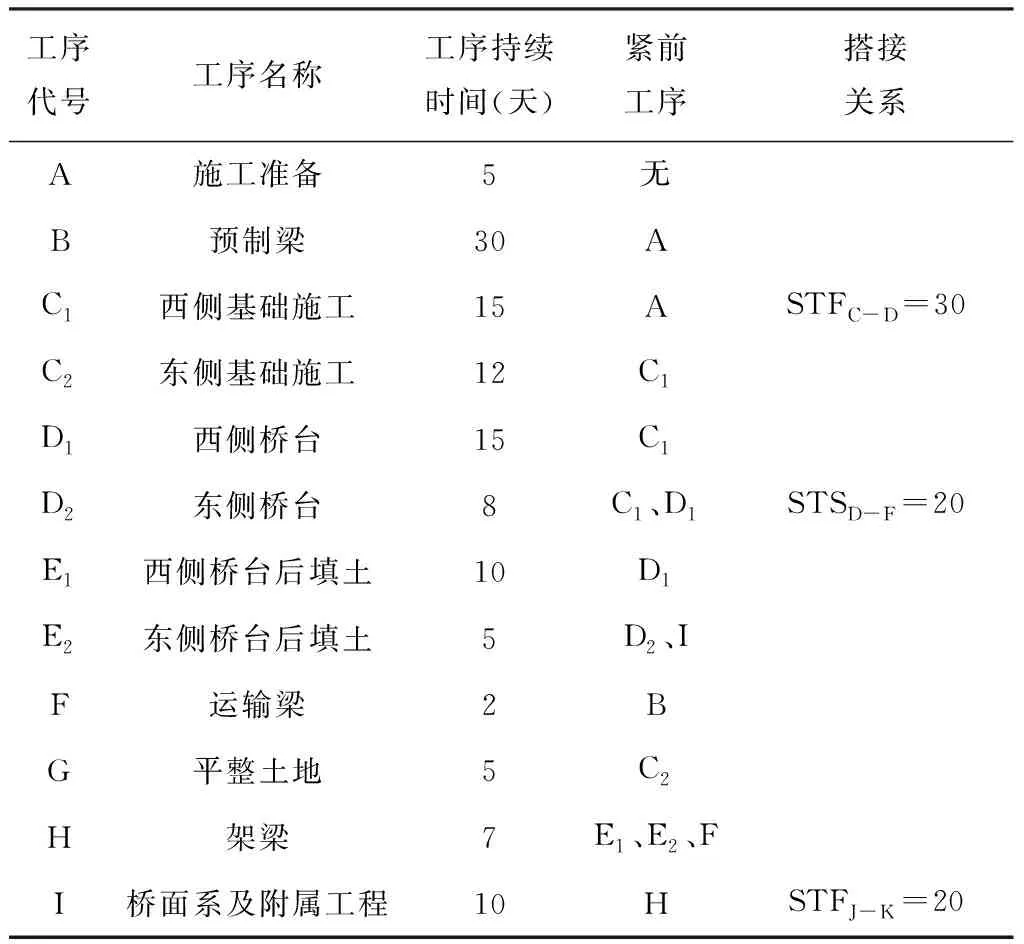
表1 高架橋施工工序及施工時間一覽表

初始施工方案的流水作業網絡計劃圖及各個工序的參數計算結果如下圖6所示。

由圖可知，該高架橋工程總工期為76天，其中關鍵線路為St→A→C1→C2→D2→E2→H→ I→Fin。關鍵工序C2和其緊前工序C1之間存在STF的搭接關系，與其緊后工序D2之間存在STS的搭接關系，根據關鍵工序分解優化定理可將工序C2進行分解。結合本實例，分解工序C2實際上就是將基礎施工的施工段重新劃分，可將工序C2拆分為兩個具有FTS=0的順序工序，即將東側基礎施工劃分為兩個施工段，則基礎部分被劃分為C1、C2、C3共三個施工段。顯然，工序H也具備可分解的條件，故可將工序H劃分為兩個具有FTS=0的順序工序H1和H2。分解優化后的流水作業網絡圖如圖7所示。

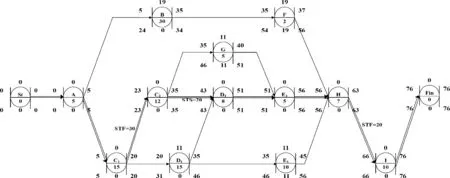
圖6 高架橋流水施工初始方案GPRs網絡圖

圖7 高架橋分解優化施工方案GPRs網絡圖

優化后該高架橋項目施工總工期縮短為68天，關鍵線路為St→A→C1→D1→D2→E2→H1→ I→Fin。施工段重新劃分之后，工序D1和D2的總時差分別增加為11天和4天，工序J2的總時差增加為13天，工序F的總時差增加為1天。由此可見，分解優化定理具有很強的應用性。對于一些應用流水作業原理施工的大型重復性建設項目，分解優化定理對其施工段的劃分具有重要意義。

5 結語

本文發現了傳統GPRs搭接網絡計劃方法中的一些新的奇異現象，如在某一可分解關鍵工序中加入一休息時間或分解關鍵工序，總工期反而縮短，這些奇異現象分別稱為咖啡時間悖論和關鍵工序分解悖論。通過對這些悖論形成原因進行分析發現，在沒有增加任何資源的情況下，甚至增加了休息時間，總工期反而縮短。說明傳統GPRs搭接網絡計劃的總工期計算結果在某些情況下存在帕累托優化改進，需要進行更科學的優化，對此，本文提出了關鍵工序的分解優化定理。在對工序分解進行拓展分析過程中總結并又提出了總時差分解優化定理，通過對工序的合理分解來最大程度上優化工序的總時差分布，并通過算例表明這些方法的有效性和簡便性。總時差分解優化定理說明了GPRs網絡計劃中的分解優化不僅僅適用于關鍵工序，對某些非關鍵工序也同樣適用。本文還將分解優化定理同流水作業原理相結合，通過實例說明了分解優化原理在流水作業施工段分解方面的實際可操作性，為項目資源優化提供了更科學的理論依據，從而有利于項目的資源優化和降低成本。