單邊Lipschitz時滯系統的H∞函數觀測器設計*

周誠來， 蔡秀珊

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

0 引 言

實際生活和工程應用中,時滯現象常引起系統的不良反應甚至破壞系統的穩定性,因此希望對時滯系統設計一個控制器，使之穩定[1-3].另一方面,系統的狀態估計也是控制研究的一大主題.外部未知干擾的存在不僅影響系統本身的狀態變化,更影響了狀態觀測的準確性.Kalman濾波法[4]與H∞濾波法[5]是常用的兩類觀測器設計方法.值得注意的是,若用H2范數作為系統的性能指標,特別是存在不確定項或者外部干擾的系統,將不能保證其魯棒性.因此,本文考慮設計一類H∞觀測器.

對于非線性系統,漸進觀測器可以精確地估計系統的狀態[6-14].現有觀測器設計大多針對于滿足Lipschitz條件的一類非線性系統,設計方法存在保守性,因而,2006年文獻[15]提出了單邊Lipschitz概念.此后對單邊Lipschitz及準單邊Lipschitz系統的觀測器設計得到了一些研究成果[16-20].

然而,對于非線性時滯系統滿足單邊Lipschitz條件的H∞函數觀測器設計還未見報道.因此,本文考慮設計一類可有效抑制外部干擾的非線性時滯系統的H∞函數觀測器.同時,還希望所設計的觀測器具有靈活性：既可以是全維的，也可以是降維的.對于降維的觀測器,則期望尋求一種簡單的設計,且能通過統一的觀測器設計算法得到.研究成果將與一類Lipschitz非線性觀測器[21]作比較.

1 系統描述

考慮如下非線性時滯系統:

(1)

式(1)中:x∈Rn,u∈Rm,y∈Rp分別為系統的狀態、輸入和輸出;xτ(t)是x(t)的滯后時間為τ的滯后狀態;ω(t)∈Rs為外部噪聲或干擾;A∈Rn×n,B∈Rn×n,C∈Rp×n,D1∈Rn×s,D2∈Rp×s為已知實矩陣;函數Φ(x,u):Rn×Rm→Rn是分別關于變量x,u連續的非線性函數.本文假定(A,C)可觀測,且C為行滿秩矩陣,初始條件ψ(t)在區間[-τ,0]上連續,并要求非線性函數Φ(x,u)滿足以下2個條件：

定義1(單邊Lipschitz條件[15]) 設O為包含原點的區域,若存在ρ∈R,使得對?x1,x2∈O,有

〈Φ(x1,u)-Φ(x2,u),x1-x2〉≤ρ‖x1-x2‖2,

(2)

則稱非線性函數Φ(x,u)滿足單邊Lipschitz條件.其中,稱標量ρ為單邊Lipschitz常數,可取正值、負值或0.

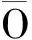
(Φ(x1,u*)-Φ(x2,u*))T(Φ(x1,u*)-Φ(x2,u*))≤

β‖x1-x2‖2+γ〈Φ(x1,u*)-Φ(x2,u*),x1-x2〉,

(3)

則稱非線性函數Φ(x,u)滿足二次內部有界條件.其中,稱標量β,γ為二次內部有界常數.

2 H∞函數觀測器設計

2.1 觀測器形式

針對系統(1),考慮如下形式的觀測器:

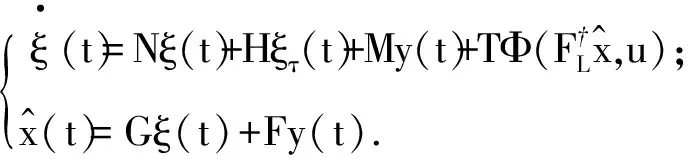
(4)

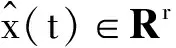
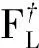
由系統狀態x(t)和觀測器狀態ξ(t)得到觀測誤差為

ε(t)=ξ(t)-Tx(t).

(5)

對式(5)兩邊關于t求導,得到ε(t)的動態方程

(HT-TB)xτ(t)+TΔΦ+Dω(t).

(6)

式(6)中:

(7)

D=MD2-TD1.

(8)

且得到估計狀態為

(9)

若待定矩陣滿足下列3個等式：

NT+MC=TA,

(10)

HT=TB,

(11)

GT+FC=FL,

(12)

即

(13)

則由式(6)和式(9)得

(14)

式(14)中,e(t)為觀測狀態與系統實際狀態之間的觀測誤差.

2.2 待定矩陣可解性

對于方程(13)解的存在性問題,可利用矩陣方程理論和矩陣廣義逆[22]的相關性質定理.對于負定(半負定)矩陣Y,記作Y<0(Y≤0).

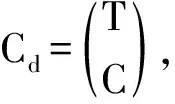
(15)

式(15)中:TG∈Rn×r;CG∈Rn×p.于是

(16)

秩條件1

(17)

若方程(13)滿足秩條件1且Δ2為列滿秩矩陣,則方程(13)存在可行解.并且

(18)

式(18)中,Y1,Y2,Y3為任意r×(r+p)維實矩陣.

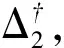
(19)

最后得到觀測器中各待定矩陣的表達式：

(20)

3 主要結果

這一節,基于線性矩陣不等式(linear matrix inequality,LMI)理論,主要解決系統(1)的H∞觀測器設計問題,即觀測誤差應滿足以下2個性質：

性質1在ω(t)=0時,觀測誤差e(t)=Gε(t)能漸近收斂于平衡點.由表達式易知,當誤差系統狀態ε(t)漸近收斂于平衡點時,e(t)也漸近收斂于平衡點.

性質2在ω(t)≠0時,?ω(t)∈L2[0,∞),在假設誤差動態系統的初始狀態為0的情況下,ε(t)=0,?t∈[-τ,0],且對于任意給定的μ>0滿足H∞性能指標

‖e(t)‖2<μ‖ω(t)‖2.

以下是本文的主要結果:

定理1若非線性函數Φ(x,u)滿足式(2)和式(3),并且存在標量τ1,τ2>0,2個正定矩陣P,Q和適當維數的矩陣N,M,H,G和F,使得式(13)有解且滿足

(21)

證明 取Lyapunov-Krasovskii泛函

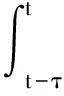
(22)

令ζ=(ε(t),ετ(t),ΔΦ,ω(t))T,則V沿著誤差動態系統(14)軌線的導數為

ε(t)TQε(t)-ετ(t)TQετ(t)=

(23)

由非線性函數滿足單邊Lipschitz條件(2)得

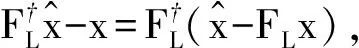
則?τ1>0,有

(24)

同理,因非線性函數滿足二次內部有界條件(3),故?τ2>0,有

(25)

令

(26)

將式(26)的右端與式(24)和式(25)的左端相加,利用條件(21)得J≤0,即

(27)

對于式(27),當干擾ω(t)=0時,根據Lyapunov穩定性定理知誤差系統漸近穩定.因此,性質1成立.當干擾ω(t)≠0時,對式(27)兩邊積分后得

(28)

由于H∞性能指標條件下要求誤差動態系統為零初始狀態,即ε(t)=0,?t∈[-τ,0],故V(0)=0,于是

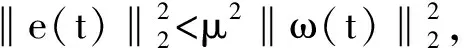
‖e(t)‖2<μ‖ω(t)‖2.

從而性質2成立.定理1證畢.

定理1中的矩陣不等式(21)并不是一個LMI,目前不能在MATLAB LMI toolbox中求解.這是因為矩陣的(1,1)位置中含有2個矩陣變量的乘積項NTP和PN.下面分析如何將矩陣不等式(21)轉化為線性矩陣不等式.

令X=PY1,則

(29)

為線性的.

于是得到如下基于定理1的LMI：

(30)

式(30)中,Σ11如式(29)所示.

經過前面的理論分析,證明了本文所設計的觀測器的存在性.下面的算法將具體給出本文所設計的觀測器的計算步驟.

算法1

步驟1：給定行滿秩矩陣FL∈Rr×n,選取合適的矩陣T∈Rr×n,判斷秩條件1,若滿足,則進入下一步,否則重新選取矩陣T.

步驟3：給定適當的Y3,由式(20)中的第3,4,5式確定G,F和H.

步驟4：對于給定的衰減度μ>0,解LMI(30),若式(30)有解P,X,τ1,τ2,則進入步驟5,否則調整T,重回步驟1.

步驟5：得到Y1=P-1X,并且通過式(20)的第1,2式得到M,N.系統(1)的H∞觀測器設計完畢.

4 算例仿真

本文所設計的觀測器既可以是全維的也可以是降維的,因此在算例仿真中,筆者安排2個對比方案來驗證本文觀測器的有效性.例1為全維觀測器與文獻[21]的對比,例2為全維與降維觀測器之間的對比.

例1全維觀測器比較

文獻[21]中機器人模型的狀態空間描述如下：

其中:Jm,Jl,θm,θl,ωm,ωl分別代表電機的轉動慣量、連桿的轉動慣量、電機轉動角位移、連桿角位移、電機轉動角速度和連桿角速度;m表示機器人質量;h表示連桿長度;g為重力加速度;k,B,Kτ為模型轉換系數.考慮如下非線性時滯模型：

y(t)=Cx(t)+D2ω(t).

干擾信號如圖1所示.

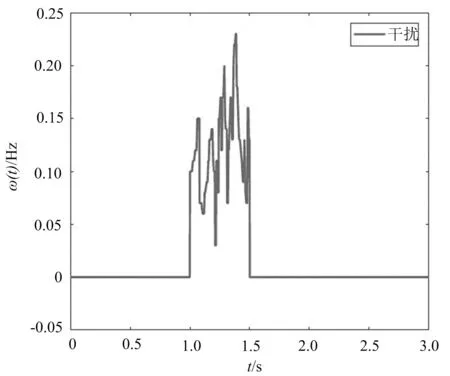
圖1 外部干擾信號

由于非線性函數Φ(x,u)滿足單邊Lipschitz條件和二次內部有界條件,故可選取一組(ρ,β,γ)=(-9,11.088 9,-1),利用算法1,得到相應的增益矩陣分別為：

H=I4;

且得到對應的正數τ1=0.422 6,τ2=0.258 9.

用本文設計的觀測器分別觀測機器人的電機轉動角位移和連桿角位置,結果如圖2所示.

圖2 電機轉動角位移和連桿角位置的真實值與觀測值

圖3 針對電機的不同觀測器觀測效果對比

圖4 針對連桿的不同觀測器觀測效果對比

定理1推論2[21]電機轉動角位移觀測誤差對比θm的誤差上界/radθm的誤差下界/rad5.614 3-0.124 27.000 0-7.620 8連桿角位移觀測誤差對比θl的誤差上界/radθl的誤差下界/rad5.579 6-8.991 422.950 8 -24.581 0增益矩陣數量級比較10kk=2k=3誤差收斂時間/s(‖e‖≤1)0.975 01.112 5

注2文獻[21]中的系統模型并未考慮外部干擾信號輸入的情況,本文設計的觀測器不僅考慮了上述情況,觀測效果也比較好.

例2降維與全維觀測器比較

本例用機器人的模型,比較本文設計的降維觀測器與全維觀測器之間的區別.降維觀測器設計方法如下：

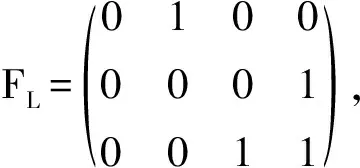
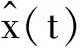
同樣選取幾項指標,對于全維觀測器和降維觀測器的數據比較記錄在表2中.對于收斂時間的統計,選取誤差精度為0.1,提取介于穩定在[-0.1,0.1]的初始點.

圖5 狀態ωm的實際值和觀測器及觀測誤差

圖6 狀態ωl的實際值和觀測器及觀測誤差

圖7 狀態θl的實際值和觀測器及觀測誤差

指標ωm的誤差上界/(rad5s-1)ωm的誤差下界/(rad5s-1)ωl的誤差上界/(rad5s-1)ωl的誤差下界/(rad5s-1)θl的誤差上界/(rad5s-1)θl的誤差下界/(rad5s-1)收斂時間/s誤差ωm誤差ωl誤差θl全維2.881 5-2.401 22.630 5-2.073 01.231 34.145 75.635 112.581 912.581 9降維0.791 4-0.249 11.414 5-0.201 30.215 2-0.025 71.552 711.841 612.095 5

由表2可知,在例2中,相對于全維觀測器,降維觀測器能更快地觀測到被挑選的系統狀態.并且誤差的上下界更小.

5 結 語

本文基于一類有干擾的時滯非線性系統設計H∞函數觀測器.利用矩陣方程組和Lyapunov穩定性理論得到了誤差系統的漸近穩定.所設計的觀測器既可以是全維也可以是降維的.研究成果應用到了一類機器人觀測器設計.