基于因子分析法的大學生體質健康評價指標關系研究
陳 濤 劉 軍
(1. 三峽大學 體育學院, 湖北 宜昌 443002; 2. 三峽大學 理學院, 湖北 宜昌 443002)
在校大學生體質健康測試已經成為高校整體工作評價體系的一部分,也是我國各個高等院校常規性任務.近年來,許多研究者對大學生體質健康評價方法和模型做了深入研究.崔巴特爾、胡曉彥、崔磊等[1]將大學生的體質健康評價和運動處方與計算機技術有機地結合為一體,從有氧耐力、肌肉力量、柔韌性、靈敏及身體成分等與體質健康密切相關的幾個方面,對大學生的體質狀況進行了橫向的定性評價和個體的縱向的動評價.萬瓊[2]運用灰色控制理論中的關聯分析和數理統計方法制訂了“湖北省大學生體質健康綜合評價模型”.楊進[3]運用因素分析法及定性定量結合法,分析了影響武漢音樂學院大學生體質健康的關鍵因素,認為影響因素依其重要性遞減排列為個人、學校、社會、家庭.王明俊、吳亮等[4]建立了評價指標與體質健康總分之間的多元線性回歸模型,通過分析評價指標與總分之間的相關性來指導教師制定教學訓練計劃.劉利、周金鎖、程昊、朱家明等[5]使用系統聚類、單因素方差分析和判別分析等方法,建立BMI分級、聚類分析、方差分析和體質健康綜合評價分級等模型.這些研究針對具體學校,分別提供評價分級模型和一些教學建議,但在挖掘重要影響因子對體質健康的作用方面未做深入探討,對于各評價指標之間關系的研究還不夠具體.
本文利用三峽大學本科生2016年進行的體質健康測試的實際數據,隨機抽取部分數據作為研究樣本,應用多元統計理論因子分析法,結合統計分析軟件進行分析和研究,提取出與體質健康水平密切相關的3個公共因子并分析其貢獻率.結果顯示,通過加強學生生理發育與基本身體素質、提升爆發力以及柔韌性,可以有助于提高學生體質健康的測試成績,以期為高校體育教學提供參考.
1 評價指標選擇與正交因子模型建立
1.1 評價指標選取
根據《學生體質健康(實行方案)》的要求,選取研究對象的身高、體重、肺活量、50 m跑、1 000 m跑、立定跳遠、坐立體前屈等7個有代表性的指標作為體質健康評價指標,進行綜合體質健康評價.
1.2 因子分析多元統計評價模型的建立
根據《國家學生體質健康標準》和運動生理學相關理論,選取出可觀測的p=7個指標x1,x2,…,x7,構成p維可觀測隨機向量:x=(x1,x2,…,xp)T,其均值向量為μ=(μ1,μ2,…,μp)T,該p維隨機向量的p×p的協方差矩陣記為∑=(σij).選取m個不可觀測因子指標F1,F2,…,Fm作為公共因子,從而建立因子分析模型如下:
(1)
其中:F=(F1,F2,…,Fm)T為公共因子向量,ε=(ε1,ε2,…,εm)T為特殊因子向量,差矩陣記為A=(aij),為p×m因子載荷矩陣.根據研究問題背景,假定該因子模型(1)是一個正交因子模型,也即下列條件成立.
E(F)=0;E(ε)=0;Var(F)=I;
Cov(F,ε)=E(FεT)=0 (2)
上述式(1)和(2)構成學生體質健康評價的正交因子分析模型.
2 觀測對象體質健康因子模型構建及統計結果分析
隨機選取三峽大學水利與環境學院本科生2016年體質健康測試的n=134名男生的測試數據為樣本,構建正交因子模型.此處,7個可觀測指標分別為:指標x1“身高”,指標x2“體重”,指標x3“肺活量”,指標x4“50 m跑”成績,指標x5“立定跳遠”成績;指標x6“坐立體前屈”成績,指標x7“1 000 m跑”成績.步驟如下.
Step 1:對原始數據進行標準化變換
對參與因子分析的p=7個評價指標x1,x2,…,x7進行標準化變換,獲取相應的標準化指標數據.設第i個指標xi在第j個被觀察個體上的觀測值為xij,i=1,2,…,p;j=1,2,…,n.且第i個指標的樣本均值和樣本標準差分別為:
于是得到第i個指標xi的標準化指標為:
相應得到各樣本數據的標準化樣本數據為:
Step 2:計算相關系數矩陣及相關性統計檢驗
相關系數矩陣為R=(rij)p×p.rij是第i個指標與第j個指標變量的樣本相關系數,rii=1,rij=rji.
利用SPSS統計分析軟件,可以計算得到這7個評價指標的樣本相關系數矩陣R,見表1.
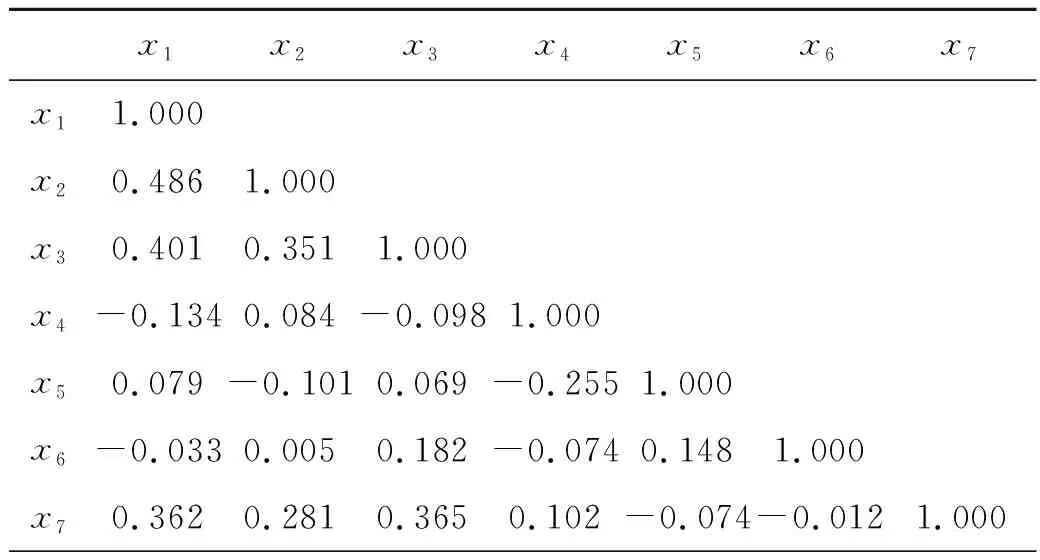
表1 7個體質健康評價指標的樣本相關矩陣
1)體質健康評價指標之間相關性分析
相關系數能夠用來評判人們的經驗判斷,幫助發現評價指標間的相互依賴和關聯關系,其絕對值反映兩個有相關關系指標之間關聯的密切程度.由于樣本容量的影響,相關系數必須經過檢驗才能使用.
根據樣本相關矩陣表1可知:學生體重與身高顯著相關;肺活量與身高顯著相關;立定跳遠與身高、坐立體前屈與身高顯著不相關.而且立定跳遠與坐立體前屈也顯著不相關.所以身高、立定跳遠、坐立體前屈這3項指標之間幾乎沒有任何聯系.從表1各個指標間線性相關性的顯著性檢驗結果看出:坐立體前屈、肺活量和立定跳遠存在一定相關性,但是與除此之外(除去肺活量和立定跳遠兩個指標外)的其他各個指標相關系數的檢驗的p值都較大,該指標與其他各個指標的相關性檢驗并沒有通過,所以坐立體前屈與其他各個指標之間不具有明顯的相關.
2)評價指標體系綜合相關性討論
針對上述觀測對象,計算得到的KMO檢驗和Bartlett球形檢驗的結果見表2.

表2 KMO檢驗與Bartlett球形檢驗
根據表2可以看出,KMO適應性檢驗的統計量等于0.641,說明針對研究問題中的觀測個體應用因子分析法是比較合適的.同時Bartlett球形檢驗的p值近似等于0.000,說明利用因子分析模型進行學生體質健康評價是合理可行的.
Step 3:應用主成分法,選擇m個公共因子,提取因子載荷矩陣
計算評價指標樣本相關矩陣R的特征根,求出的7個特征根按照從大到小的順序,分別是λ1=2.134,λ2=1.416,λ3=0.994,λ4=0.757,λ5=0.722,λ6=0.545,λ7=0.432.設相應于每個特征根的特征向量分別是u1,u2,…,u7,且ui=(u1i,u2i,…,u7i)T,i=1,2,…,7.求出的體質健康評價指標的樣本相關矩陣R的前3個最大特征根分別為λ1=2.134,λ2=1.416,λ3=0.994.
其中只有前3個特征根幾乎都是大于1的,所以選取m=3個公共因子進行學生體質健康的因子分析和評價.提取出的p×m的因子載荷矩陣為:
(3)
Step 4:應用最大方差法,進行因子旋轉求取旋轉因子載荷矩陣
通常情況下,因子載荷矩陣(3)較難給出公共因子在體質健康方面的有意義合理解釋,所以,對式(3)提取出的因子載荷矩陣作旋轉變換,應用最大方差旋轉法進行因子載荷矩陣的旋轉,得到旋轉后的因子載荷矩陣見表3.
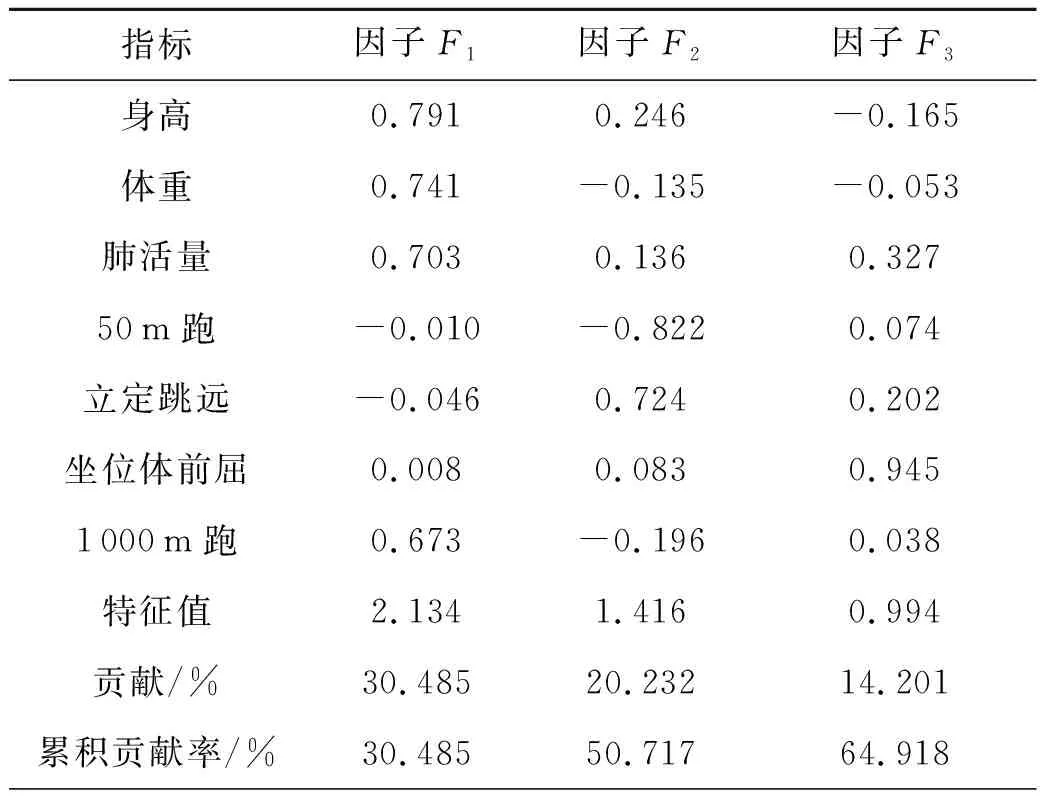
表3 旋轉后的因子載荷矩陣、特征值和因子方差貢獻率表
3 體質健康評價指標間關系的討論
3.1 提取出的因子特征
從表3可以看到:
1)在提取出的3個公共因子中,可觀測指標“身高”、“體重”、“肺活量”和“1 000 m跑”都與第1個因子具有很高的相關度,而這4個測試指標具有的共同點是反映了身體基本發育和生理體質狀況,所以該公共因子可稱為“生理發育與體質”因子.
2)可觀測評價指標“50 m跑”和“立定跳遠”與第2個公共因子的相關度很高,所以第2個因子概括和代表了50 m跑和立定跳遠具有的共同特征,反映了受測試個體的身體爆發力方面的運動素質,所以第2個因子稱為“爆發力”因子.
3)坐立體前屈指標與第3個因子的相關度最高,達到94.4%,而除此之外的其他指標與第3個因子的相關度都很低.所以第3個因子很好地反映了身體的柔韌性素質,因此第3個因子稱為“柔韌性”因子.
3.2 提取出的特征因子的貢獻率分析
從表3中看到,第1個因子對于全部體質健康評價指標的方差貢獻率達到30.485%;第2個“爆發力”因子對于全部體質健康評價指標的方差貢獻率達到20.232%,是貢獻第二多的因子;第3個“柔韌性”因子對于全部體質健康評價指標的方差貢獻率達到14.201%,是貢獻第三多的因子.前3個因子的累積貢獻率更是達64.918%.因此,應用因子分析模型對觀測樣本進行分析是較為合理和科學的.
3.3 因子分析結果對提高體質健康素質的參考意義
從表3還可看到,前面3個因子對全體評價指標的貢獻率近70%,這3個因子所代表的特征就是在體育課程等教學活動中教師應關注的重點方面.換言之,為有效提高學生的體質健康水平,必須從提高學生的營養水平、促進學生身體正常發育生長,提高其基本身體素質,學生的爆發力等方面入手,在體育課程教學和訓練計劃中,注重對學生爆發力,柔韌性等方面的訓練,有的放矢地提高學生的體質健康水平.
4 觀測個體的因子得分及其體質健康評價
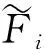
(4)
設第j個觀測對象在第i個因子上的得分值為
i=1,2,3;j=1,2,…,134 (5)
于是利用上述因子得分模型,可以得到134個個體觀測數據值(需要將樣本數據標準化之后代入式(4)和(5)計算)在兩個因子上的得分,分析各個被研究個體的體質健康狀況.
根據模型(5)對于134個觀測個體,可以得到的具體因子模型及3個因子的因子得分見表4.

表4 因子得分系數矩陣
根據表4,可得到被觀測組因子得分模型為

利用上述因子得分模型,可計算得到134名被測試個體學生中的每一名學生分別在“生理發育與體質”因子F1、“爆發力”因子F2、“柔韌性”因子F3上的具體得分,從而實現具體到對每一名學生制定提高體質健康的個性化教學方案,真正做到因材施教.
5 結 論
通過對學生體質健康評價指標的因子分析,可以得到如下結論:
1)為了有效提高高校學生的體質健康水平和相應的測試成績,相關教學職能部門和教師在體育教學的大綱和課程教學、訓練計劃的制定過程中,應該在考慮全局的前提下,重點圍繞與學生生理發育、基本身體素質、爆發力關系密切的1 000 m跑、50 m跑、立定跳遠等項目的教學和訓練.
2)要倡導學生在校日常生活中堅持日常體育鍛煉,有效促進身體正常發育,達到合理的體重狀態,獲得優良的身體形態,提高體質健康水平.
3)由于身體柔韌性是一個相對獨立的身體素質指標,所以體育教學過程中,也要重視增加學生柔韌性的鍛煉項目,提高學生身體柔韌性.同時,還可根據學生在3個因子上的得分狀況,制定有針對性的體育教學與鍛煉計劃,有效提高學生體質健康水平.

