基于線性自抗擾的開關磁阻電機調速控制研究

，

(華南理工大學 自動化科學與工程學院，廣州 510641)

0 引言

開關磁阻電機(Switch reluctance motor，SRM)是繼直流電機與交流電機之后發展起來的一款新式無極調速電機。由于其具有結構簡單、控制方式靈活、系統能量轉換效率高等諸多優點，因此受到了現代電氣驅動領域的廣泛關注。但是由于開關磁阻電機內部呈現雙凸極結構以及磁路易飽和的特點，使得磁鏈、轉矩均為轉子位置和電流的非線性函數。因此開關磁阻電機調速系統是一個變參數、非線性、強耦合的時變復雜系統[1]。在線性領域具有良好控制效果的PID控制方式無法使其獲得高要求的動靜態性能。文獻[2]介紹了一種基于最優開通角的控制方法，但其性能依賴于被控模型的精確程度；文獻[3]給出了基于模糊規則的PID控制策略，但其控制效果十分依賴模糊規則，而模糊規則的建立需要操作者擁有大量實踐操作的經驗。

自抗擾控制(active disturbance rejection control，ADRC)技術是由中科院韓京清研究員在經典PID控制的基礎上改進后形成的一種新型控制方法[4]。自抗擾控制算法結構簡單，魯棒性強，可對系統受到的各種擾動進行精確估計并補償，對被控對象參數的變化及不確定性也具有很好的適應性。目前已廣泛應用于電力系統、精密器械、加工車床、化工過程和現代武器系統等領域。但是自抗擾控制器參數過多，參數整定麻煩，這限制了其進一步發展。文獻[5]給出了利用帶寬的概念將自抗擾控制器線性化的方法，從而提出了線性自抗擾控制(linear active disturbance rejection controller，LADRC)方法。與ADRC相比LARDC在保持了自抗擾控制算法優良控制性能的基礎上，簡化了算法結構，減少了控制參數數量，使參數整定更加容易，更便于進行工程應用。文獻[6]對線性擴張狀態觀測器對對象模型不確定性的估計收斂性進行了證明并給出了LADRC閉環系統的穩定性分析。

本文采用線性自抗擾控制算法設計開關磁阻電機調速系統控制器。利用系統辨識方法獲得被控對象的數學模型，根據得到的數學模型設計擴張狀態觀測器和PD控制器。通過仿真對線性自抗擾控制器的控制效果進行了驗證。

1 開關磁阻電機調速系統特性

1.1 開關磁阻電機調速系統結構

本文研究的對象是開關磁阻電機調速系統，該系統基本結構如圖1所示。

圖1 開關磁阻電機調速系統結構圖

該系統結構主要包括開關磁阻電機、功率變換器、轉子位置檢測電路、電流檢測電路和控制器5個部分[7]。轉子位置電路實時檢測轉子位置信號，并送入控制器可計算得到電機的實時轉速；功率變換器按控制器給定的策略將電源提供的能量傳遞給SRM，驅動電機運轉；電流檢測電路檢測相繞組上的電流，為系統實現電流斬波控制和過流保護提供基礎；SRM作為系統的被控對象主要完成系統中機電能量之間的轉換。

1.2 開關磁阻電機的數學模型

開關磁阻電機是一種典型的非線性系統，系統磁場空間結構復雜，使用傳統的電機性能分析方法很難得到其系統的準確模型，因此需要對其對象模型進行辨識[8]。本文利用試驗與仿真結合的方法建立被控對象的數學模型。先通過試驗采集得到系統的輸入、輸出數據，再通過數值工具離線擬合得到其近似傳遞函數模型，具體的辨識過程如下：

1)在空載情況下，以電壓脈沖信號作為控制輸入，以實際轉速作為輸出，對電機實施開環控制進行數據采集。

2)將采集得到的數據導入MATLAB中進行讀取，利用MATLAB的模型辨識工具進行辨識。

3)對估計模型進行選擇，根據實際轉速數據曲線特征，開關磁阻電機可近似為一個二階模型。對辨識得到的模型進行試驗，試驗得到的數據可以很好的擬合實際采集的數據。

本次設計最終辨識得到的被控對象的傳遞函數為：

(1)

2 控制系統設計

2.1 線性自抗擾控制基本原理

PID控制策略是一種固定狀態的控制策略，即每次整定得到的參數只對某一種狀態固定的系統有效。而對于系統結構和參數均隨時間不斷變化的非線性系統，單一狀態的PID控制策略很難在整個控制范圍取得理想的控制效果。正是在這種背景下產生了自抗擾控制策略，而高志強在自抗擾控制的基礎上利用帶寬概念提出了線性自抗擾控制策略[9]。

典型系統的線性自抗擾控制原理圖如圖2所示。

圖2 典型系統線性自抗擾控制器結構圖

由圖可知線性自抗擾控制器由跟蹤微分器(TD)、PD(比例-微分)控制器和擴張狀態觀測器(ESO)三部分組成[9]。跟蹤微分器的作用是為輸入信號安排過渡過程并提取高品質的微分信號，從而解決了傳統PID控制誤差信號選擇不合理的缺陷。引入過渡過程不僅可以提高控制器魯棒性，還可以使控制器參數適應的對象范圍更大，增強控制器的適應性。作為自抗擾控制器的核心，擴張狀態觀測器能夠在不知道系統精確數學模型的情況下，利用系統的輸入和輸出估計出被控對象各階狀態變量以及對象受到的總擾動并給與補償，從而使系統轉化為簡單的“積分串聯器型”線性系統。PD(比例-微分)控制器將跟蹤微分器的輸出與擴張狀態觀測器觀測估計之間的誤差進行線性組合構成控制量來抑制穩態誤差。通常情況下LADRC可不用設計“過渡過程”即微分跟蹤器即可得到良好的控制性能，因此LADRC控制器結構更加簡單，便于工程實現。

2.2 線性自抗擾控制器設計

以開關磁阻電機作為系統被控對象來設計線性自抗擾控制器，設計過程具體如下。

為使設計的控制器具有通用性我們設上述二階系統為如下表示形式：

(2)

(3)

針對上述系統設計線性擴張狀態觀測器(LESO)，其具體形式如下所示：

(4)

其中：β1、β2、β3是狀態觀測器的參數。通過對觀測器中的參數進行適當的調節，這個狀態觀測器的各個狀態變量zi(t)便可實時跟蹤式(4)所表示系統的各個狀態變量xi(t)(i=1,2,3)即有：

z1(t)→x1(t),z2(t)→x2(t),z3(t)→x3(t)

接著設計PD控制器。為提高開關磁阻電機調速系統的快速響應性能以及使算法便于實現，LADRC控制律采用線性組合的形式，假設

(5)

這里若忽略對的估計誤差，則式(4)所表示的系統可簡化成一個積分串聯結構，即為：

(6)

則PD控制器可設計成如下形式：

u0=kp(x*-z1)-kdz2

(7)

式中，x*表示系統給定，kd為控制器增益。

綜上所述，式(4)、(5)、(7)便構成了本次設計的線性自抗擾控制器(LADRC)，其結構如圖3所示。

圖3 線性自抗擾控制器結構示意圖

但上述LADRC形式依然有多個參數需要整定，因此文獻[9]引入了帶寬的概念來進一步簡化算法的參數設計。綜合式(6)和(7)可得系統的閉環傳遞函數為：

(8)

根據文獻[8]，可將式(9)的參數選為：

(9)

式中：ωc稱為控制器的帶寬，ξ為系統阻尼比。當ξ=1時，上式可變為：

(10)

同理我們可以求得線性擴張狀態觀測器式(5)的特征方程為：

λ(s)=s3+β1s2+β2s+β3

(11)

假設理想線性擴張狀態觀測器的特征方程為，則上下兩式對比有：

(9)

式中,ω0稱為觀測器的帶寬。

這樣通過引入帶寬的概念，LADRC控制器參數配置問題就被簡化為選取合適觀測器帶寬和控制器帶寬問題，相比于ADRC，需要調節的控制參數數量大幅減少。

2.3 線性自抗擾控制器的參數整定

因為線性自抗擾控制器是一種不依賴被控對象控制模型的控制方法，只需確定好合適的參數即可實現對被控對象的穩定控制。由前述分析可知，LADRC已將控制參數整定簡化為只需整定控制器帶寬和觀測器帶寬兩個參數即可，且二者可獨立調整。此外，控制增益的選擇也會對系統的動態特性產生影響。本節將介紹一種根據實際工程經驗總結得到的對于二階系統的參數配置方法[10-13]。

控制器帶寬調節。

1)若被控對象的數學模型已知，則可根據其模型寫出式(4)所示的狀態方程，從而可確定控制增益；若被控對象難以建立數學模型，則可利用“時間尺度”模型辨識方法辨識出系統的大致數學模型，根據其初步選取控制增益。

2)對參數和選定一個初值，然后固定不變，慢慢增加直至噪聲的影響難以滿足系統的性能要求為止。

3)再慢慢增大，直至系統難以承受噪聲的影響而產生輸出波動時，減小，然后再慢慢增大，如此反復循環調試，直至達到設定的控制要求。

4)若無論怎樣調節，都無法消除噪聲帶來的影響時，可采用在LESO輸入端增加濾波器的方法，然后重復第三步的過程確定和。

5)若在調參的過程中，系統動態跟蹤過程出現過大幅度的震蕩，則可通過調節來調節其系統的動態過程。

6)若在調參過程中控制量出現了深度飽和現象，則可根據第一步辨識得到的被控對象的時間尺度為LADRC設計“安排過渡過程”即跟蹤微分器來進行調節。

3 仿真研究與分析

3.1 仿真模型建立

在MATLAB上建立基于線性自抗擾控制器的開關磁阻電機調速系統模型，對控制器的控制效果進行仿真試驗，驗證線性自抗擾控制器的控制性能并與基于PID控制器的調速效果進行比較。

本次仿真控制的開關磁阻電機已經通過辨識得到了其數學模型為G(s)=0999/[(1.816s+1)(1.501+1)]。線性自抗擾控制器需要整定3個參數，分別是b0、ωc和ω0。根據上節介紹的參數整定方法分別整定得到b0=0.012、ωc=9,ω0=30。采樣時刻Ts=0.009s。

3.2 仿真結果

圖4顯示了給定系統額定轉速為500 r/min下，系統實際轉速的變化曲線。由仿真曲線可以看出：轉速啟動平穩且啟動時間短，啟動時間僅需0.16 s，滿足啟動控制速度快的要求，穩態運行時基本無超調，穩定時間短，只需1.026 s系統即可穩定且在穩定情況下轉速幾乎無波動。

圖4 線性自抗擾控制500 r/min啟動情況

圖5顯示了擴張狀態觀測器的輸出對系統實際輸出的跟蹤情況，由仿真曲線可以看出狀態觀測器的估計值跟蹤效果良好。

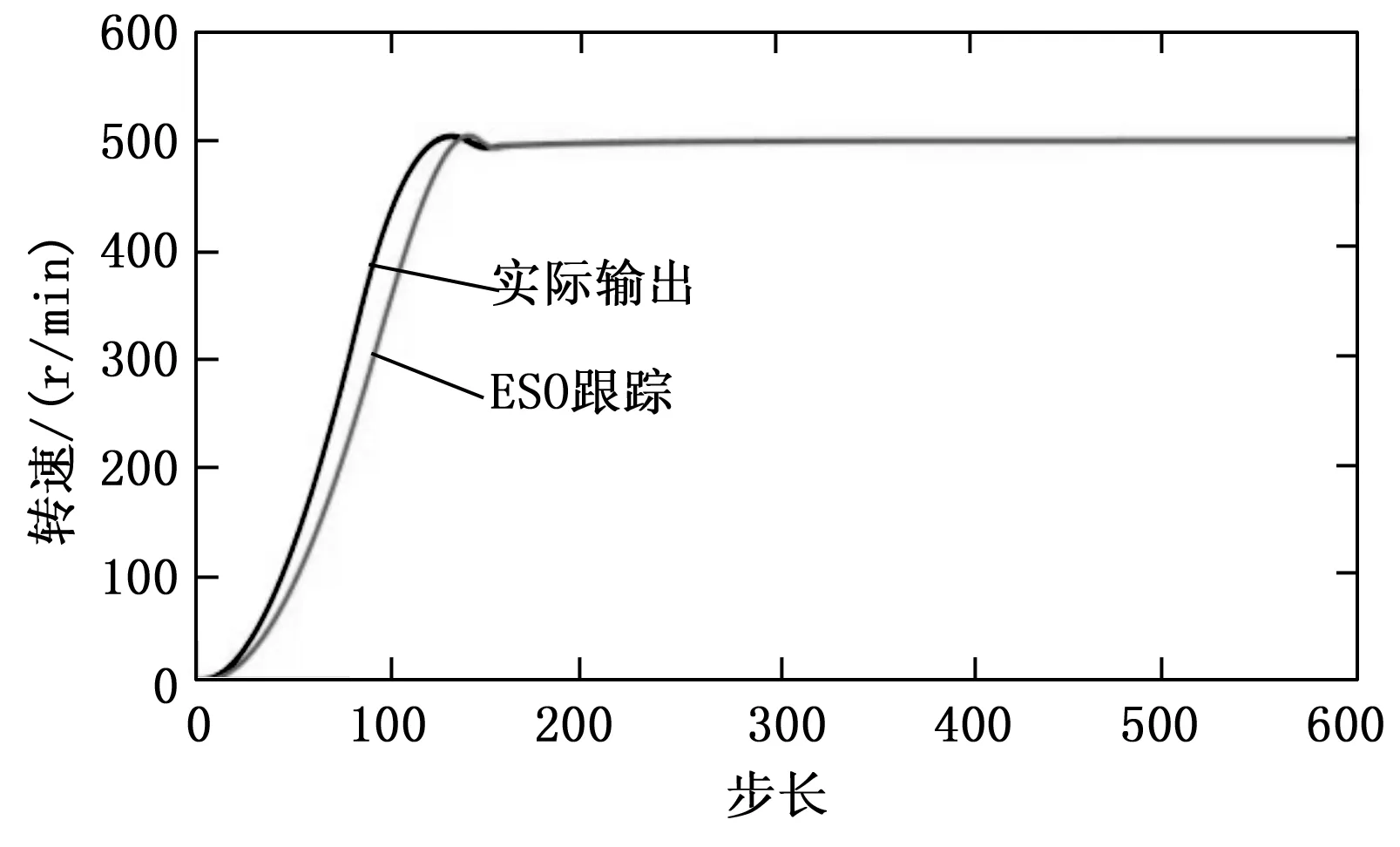
圖5 狀態觀測器估計與系統輸出曲線

在實際應用中電機的給定轉速通常會實時變化，圖6顯示了給定轉速突變時時，系統輸出的跟蹤情況。由圖可知，系統對給定突變具有很快的響應速度，且穩態精度很高，控制效果良好，顯示了基于線性自抗擾控制器的調速系統具有良好的跟蹤特性。

圖6 給定變化下的系統輸出曲線

由于開關磁阻電機變結構、變參數的特點，因此其模型在運行過程中始終處于變化之中。我們對前述得到的模型參數進行改變之后再進行試驗。圖7顯示了改變了模型參數的系統在給定轉速為500 r/min下的輸出曲線，結果顯示實際輸出仍能很快跟蹤給定值，且啟動、穩態性能良好，表明線性自抗擾控制器對于模型參數變化帶來的內部擾動也具有很好的抵抗能力。

圖7 改變模型參數后的500 r/min啟動情況

最后在同樣的條件下對使用PID控制器的開關磁阻電機調速系統進行仿真試驗，仿真結果顯示對于給定的階躍信號線性自抗擾控制系統啟動更快，只需0.09 s即可達到穩態且無超調，而PID控制系統需要3 s才能實現穩定跟蹤。其仿真曲線分別如圖8、圖9所示。

圖8 PID控制下的轉速變化曲線

圖9 線性自抗擾控制下的轉速變化曲線

4 結論

本文利用LADRC對開關磁阻電機速度環控制器進行設計。利用線性自抗擾控制器不依賴被控對象精確模型的優勢，避開了無法獲得開關磁阻電機準確數學模型的弊端。通過對基于線性自抗擾控制器的開關磁阻電機模型進行仿真并與PID控制進行比較可知：這種控制策略對開關磁阻電機具有良好的控制效果，并且由于其通過利用狀態觀測器可對系統內、外部擾動進行觀測并補償，使得該控制策略具有良好的魯棒性。因此線性自抗擾控制方法非常適合應用于開關磁阻電機這一類給定多變、非線性嚴重、擾動多的控制對象。