非視距環境下的超寬帶室內定位算法

，

(河海大學 能源與電氣學院，南京 211100)

0 引言

近年來，隨著人們需求的增長，不論是在工業領域還以日常生活中，越來越重視室內的精確定位與導航。為了滿足人們日益增長的需求，國內外研究人員將多種技術應用到室內定位領域中，例如紅外傳播技術、超聲波技術、射頻識別技術(FRID)、Wi-Fi技術、低功耗藍牙技術以及超寬帶技術[1]。超寬帶技術(UWB)是近年來新興的無線通信技術，無需用到傳統通信中的載波，利用納秒級的極窄脈沖傳輸信息，具有多徑分辨能力強、功耗低、穿透能力強等特點[2]，這些優勢使得超寬帶技術在室內定位領域有較好的發展前景。UWB定位中基于測距常用的算法有基于信號到達強度(RSSI)、到達信號角(AOA)、到達信號時間(TOA)、到達時間差(TDOA)等方法[3]。其中最常見的是TDOA算法，在該算法中有兩個主要的誤差來源：一是系統測量值誤差，包括隨機測量誤差和時鐘漂移引起的誤差兩部分，相對而言對定位結果精度的影響不大；另一個影響較大的誤差是由于信號在復雜的室內環境下傳播時，遇到多種障礙物發生反射、折射、衍射甚至穿墻而過，從而引起的非視距(non-line of sight，NLOS)誤差[4]，由于該誤差導致的額外時延對最終的定位結果影響較大，是影響定位精度的主要來源。因此，減弱非視距誤差對定位精度的影響是研究超寬帶室內定位技術的重要問題。

根據特定NLOS環境中的參數建立均方根時延擴展模型，通過額外時延和均方根時延擴展的關系計算出額外時延的參數，用估計出的額外時延參數來調整TDOA定位模型。再將重構后的TDOA模型轉化為粒子群算法中的適應度函數，從而可利用粒子群算法估計出精確的目標位置。本文提出的優化算法可以有效抑制NLOS對測量值的影響，提高室內定位的精度和算法收斂速度。

1 系統模型建立

1.1 TDOA定位模型的建立與重構

(1)

(2)

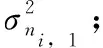
γ(t)=(1+e)t+ψ

其中，t為理想時間，e為頻率漂移，ψ為頻率偏差，假設各基站和目標節點的時鐘漂移速率保持一致，則基站i和基站1到目標節點的信號傳播時間差由于時鐘漂移引起的誤差表示為：

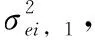
μei,1=E(τei-τe1)=μei-μe1

(3)

(4)

因此，由以上分析可知式(2)可進一步改寫為：

(5)

由此，實現了對TDOA定位模型的重構，為了得出τi,1的值，還需要計算出超寬帶信號在NLOS環境中傳播的誤差τei值。

1.2 延遲拓展參數的求解

NLOS誤差在不同的信道環境下服從指數分布、均勻分布以及Delta分布[6]。選擇延遲拓展按照其中的指數分布模型來分析非視距誤差，其概率密度函數為：

(6)

(7)

(8)

(9)

根據概率論的知識，結合式(6)和式(9)可得延遲拓展誤差τei的概率密度函數 ，其中τi,rms≥0：

由此可得τei的均值和方差分別為：

(10)

(11)

由式(10)、(11)進一步可得TDOA測量模型中的式(3)和式(4)中的參數：

(12)

(13)

1.3 目標函數的建立

(14)

其中:λ=σ2σ3…σM-1

λ2=σ3σ4…σM-1

λM-1=σ2σ3…σM-2

求解使式(14)的似然函數值最大的解，相當于求解滿足下式最小的解：

(x0,y0)=arg{min[(A-B+C-U)T(A-B+C-U)]}

為了求出此函數的最小值，用一般的解析法解此類非線性函數比較困難，且有較大誤差，為解決這一難題，本文將一種群智能優化算法——粒子群優化算法應用到最優解的求解中，將上式函數作為粒子群算法中的適應度函數，從而可通過迭代估計出目標節點的坐標值。

2 基于LS-PSO優化的NLOS定位算法

2.1 初始位置的估計

根據TDOA數學模型式(1)并將其進行線性化處理可得：

(15)

(16)

其中:Ri,1=Ri-R1

將上式(15)、(16)相減，得：

(17)

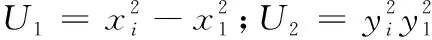
xi,1=xk-x1；yi,1=yk-y1

在式(17)中，將x0，y0，R1當作未知變量，那么該式則成為線性方程租，此線性方程組的解則作為目標節點的初始估計位置。將TDOA測量值看作實際值代入到下列式子，采用最小二乘法[8]估計出的目標節點初始粗略位置為：

其中:

2.2 基于粒子群算法的NLOS定位

粒子群優化算法(particle swarm optimization，PSO)是一種群體仿生智能算法，起源于對鳥群覓食過程中遷徙和聚集的模擬[9]。算法描述為：在一個給定的D維區域中，有N個粒子組成的群體x=[x1,x2,…,xN]，每一個粒子都視為潛在解且有自身的位置和速度信息，每個粒子的位置坐標為xi=[xi1,xi2,…,xiD]，速度表示為vi=[vi1,vi2,…,viD]。PSO經典算法是在D維空間中隨機初始化一群粒子，此時的每個粒子都視為潛在解，將每個粒子的位置坐標代入適應度函數中，通過適應度函數值反映每個粒子的優劣情況；在每一次的迭代中，粒子根據局部最優解和全局最優解來更新當前的位置和速度，從而在給定區域內運動，在迭代過程中群體里的所有粒子會向著適應度值最佳的粒子的方向運動，直到經過若干次迭代后找到最優解；局部最優解是指每個粒子在經過目前的迭代次數后所找到的自身的最優解，可以表示Pbesti=[pi1,pi2,…,piD]，全局最優解是指全部粒子在經過目前的迭代次數后所找到的整個離子群的最優解，可以表示為Gbest=[g1,g2,…,gD]；在經過一次自身最優解和群體最優解的更新過后，每個粒子再將自身目前的速度和位置代入下面兩個公式更新速度和位置：

vi(t+1)=ω*vi(t)+c1*rand()*(Pbesti-xi(t))+

c2*rand()*(Gbest-xi(t))

xi(t+1)=xi(t)+vi(t+1)

式中，t為當前迭代次數；ω為慣性權重，其值表示粒子對目前速度、狀態的依賴程度；c1，c2為學習因子，取值為2；rand()為服從均勻分布的隨機數[9]。

由于粒子群算法隨機初始化一群粒子，導致其初始收斂速度慢的缺陷[7]，在本文2.1節通過最小二乘法得出目標節點的初始估計位置可以有效解決該問題，較少了收斂時間，則粒子群算法的初始位置可表示為：

xi1=Za(1)+rand()

xi2=Za(2)+rand()

其中:rand()的作用是產生分布在[0，1]內的隨機數，可以使粒子群算法的初始粒子在最小二乘法估計出的位置附近開始搜索，達到了提高收斂速度的目的。本文中使粒子群算法停止的條件是最大迭代次數，設置的最大迭代次數設置為itermax=100。

對于算法中的慣性權重ω，一般情況下按照線性遞減的方式變化，若函數一旦進入局部極值點就很難跳出，從而陷入局部最優[9]。文獻[10]指出，當慣性權重ω服從正態分布時，算法的全局搜索能力較傳統的線性遞減時有明顯提高，可避免陷入局部最優，能夠有效協調全局和局部搜索在算法中的權重。高斯函數服從正太分布，因此本文使慣性權重按照高斯函數遞減，表示為：

其中:κ為一常數，κ的大小影響了曲線的變化率，本文選取κ=0.2。

基于改進粒子群算法的NLOS定位算法流程為：

3)將TDOA定位模型轉化為粒子群算法中的適應度函數，把修正后的TDOA參數代入到適應度函數中；

4)利用改進慣性權重的粒子群算法進行迭代求解目標節點的精確位置。

3 仿真結果與分析

本文采用MATLAB對上述的理論進行驗證，模擬的仿真環境如下：假設室內環境比較復雜，有多種障礙物和人員的走動，無法檢測到LOS信號，只能得到NLOS信號；在50 m×50 m室內二維平面中，有3個基站和一個目標節點，基站坐標已知且所有基站和目標節點位于同一個平面中。將本文提出的LS-POS算法與兩步最小二乘法(2LS)和文獻[11]提出的Chan-Taylor算法進行比較，采用均方根誤差作為評價定位精度的指標：

由圖1可以看出隨著測量噪聲誤差的增大，3種算法的均方根誤差都相應增大，但本文提出的LS-PSO算法定位性能要優于2LS和Chan-Taylor算法。最小二乘法是一種非迭代定位算法，無法在迭代的過程中逐漸減小誤差，因此兩步最小二乘法的定位性能較差。

圖1 測量噪聲標準差和均方根誤差的關系

圖2所示為在非視距環境下，改變均方根時延拓展中的參數T1使其逐漸增加，代表著非視距誤差也相應的增加，由圖可以看出隨著非視距誤差的增加，3種算法的均方根誤差都受到了較大影響，出現了較大的上升幅度，但相比如另外兩種算法，本文提出的LS-PSO算法受到的影響最小。Chan-Taylor算法受到的影響較大，定位結果與2LS相當，這是因為Chan算法能夠精確定位的前提是TDOA誤差的均值要盡量小，否則定位結果將會受到很大影響[12]，在存在非視距誤差的環境中TDOA誤差服從的是正均值的高斯分布，且此均值較大，因此Chan定位精度明顯下降，Taylor又是以Chan算法的定位結果為初始值，從而導致該算法在非視距環境下性能的降低。

圖2 非視距誤差和均方根誤差的關系

圖3為本文提出的基于LS初值估計的POS算法和經典PSO算法在收斂能力上的比較，橫軸表示算法的迭代次數，縱軸表示粒子群算法中的適應度值。由圖可以看出，LS-PSO算法在第23次迭代即可收斂，達到了最佳的適應度值，而經典PSO算法在41步才達到最佳適應度值，因此LS-PSO算法相對于經典PSO算法提高了收斂速度。

圖3 LS-PSO和經典PSO算法收斂速度的比較

圖4展示了粒子群算法中慣性權重的改進對定位結果的優化作用，當慣性權重按照高斯函數變化，定位結果明顯優于按照線性遞減的策略，改善了粒子群算法易陷于局部最優的缺點，從而提高了定位精度。圖5為慣性權重按照兩種策略變化時收斂速度的比較，當慣性權重按照高斯函數變化時，經過23步迭代即可收斂，而當慣性權重按照線性遞減策略變化時，需要經過37步迭代才收斂。因此，對粒子群算法中的慣性權重參數進行調整，使其按照高斯函數變化，可以顯著改善算法易陷入局部最優的缺陷、提高定位精度，并且可以加快算法的收斂速度，優化了算法的性能。

圖4 兩種策略定位精度的比較

圖5 兩種策略收斂速度的比較

4 結語

本文研究了非視距環境下超寬帶室內定位算法。首先對NLOS室內環境中的TDOA定位模型重構；然后由均方根時延拓展估計出NLOS誤差的均值和方差，對重構后的TDOA模型參數作調整，建立適應度函數；最后通過LS-PSO算法估計出目標節點的位置坐標，并與2LS和Chan-Taylor算法進行定位性能的比較。仿真結果顯示，本文提出的LS-PSO算法可以較好的抑制非視距誤差，提高非視距環境下的定位精度，且可以有效提高算法的收斂速度。此外，除了在超寬帶室內定位中，本文提出的算法也可應用在非視距環境下的其他無線定位技術中，提高其定位精度，因此具有一定的實際意義。