“給值求角”問題解法探討

曾宇嘉

(河北省任丘市第一中學 062550)

解決“給值求角”問題分兩步：第一步，求該角的某種三角函數值；第二步，解三角方程，根據角的范圍確定角的大小．

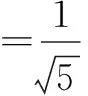
而α,β都是銳角，0<α+β<π,

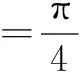
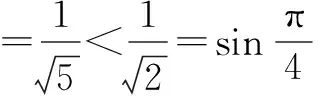
說明除了根據不等式的性質確定角的范圍外，有時候要根據三角函數值的正負號進一步地縮小角的范圍，有時候還根據三角函數值的大小進一步地縮小角的范圍．

其實，0<α+β<π，本題中可以求α+β的余弦或正切更簡單．

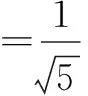
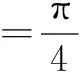
由此看來解決“給值求角”問題要注意兩步之間的關系，如果求的三角函數不適當，就會給第二步確定角的范圍帶來很大的麻煩．

分析思路一，α=(α-β)+β，2α-β=(α-β)+α，用和角公式Tα+β先求tanα，再求tan(2α-β)；思路二，2α-β=2(α-β)+β，所以先用倍角公式T2α求tan2(α-β)，再用和角公式Tα+β求tan(2α-β)．

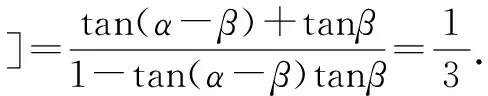
而tan(2α-β)=1,

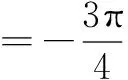
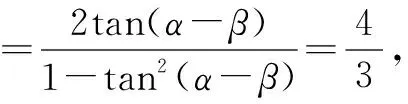
tan(2α-β)=tan[2(α-β)+β]

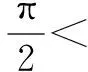
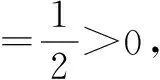
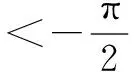
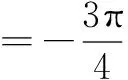
有時“給值求角”問題就象例2的思路二一樣讓人頭痛，解決“給值求角”問題分兩步：第一步，求該角的某種三角函數值；第二步，解三角方程，根據角的范圍確定角的大小．需要注意：1.求該角的某種“適當的”三角函數值，“適當的”三角函數值可以幫我們縮小角的范圍；2.求該角的某種三角函數值，要選擇適當的角的變換與組合，原則是有利于縮小角的范圍；3.縮小角的范圍，除了根據不等式的性質確定角的范圍外，有時候要根據三角函數值的正負號進一步地縮小角的范圍，有時候還根據三角函數值的大小進一步地縮小角的范圍．為了確定角的范圍，我們寧可多求一些三角函數值，如果只利用不等式的性質確定角的范圍，過程越多，范圍越大，問題越多．