關(guān)于高中數(shù)學(xué)變形類試題的教學(xué)研究

王佳美

(北京市北京龍文教育 100096)

據(jù)實(shí)來說，高中數(shù)學(xué)就是以高考為圓心的數(shù)學(xué)教學(xué).縱觀近年的高考題目，題型越來越新穎，技巧性也越來越強(qiáng)，而變形技巧是其中較為常見的.熟練掌握變形解題技巧，可讓解題過程變得更加的理性，讓做題的效率更高.這對(duì)于即將面臨高考的學(xué)生來講，可以大大地增強(qiáng)學(xué)生們學(xué)好數(shù)學(xué)的信心，提高對(duì)數(shù)學(xué)學(xué)科的學(xué)習(xí)興趣.教育的目的是培養(yǎng)學(xué)生獨(dú)立思考和獨(dú)立解決問題的能力，這是時(shí)代的要求，更是一個(gè)人終生學(xué)習(xí)的要求.變形試題的技巧性學(xué)習(xí)在學(xué)生的思維能力培養(yǎng)方面起到了非常重要的作用.

一、通過對(duì)變形技巧的學(xué)習(xí)，提高學(xué)習(xí)興趣

對(duì)于大部分高中生來說，他們比較善于解答標(biāo)準(zhǔn)類型的題目.因?yàn)檫@類題目考查的是學(xué)生們基礎(chǔ)知識(shí)的掌握程度，也就是我們平常所說的“死題”，按照原有的公式、概念一一代入就可以完成任務(wù).但從長(zhǎng)遠(yuǎn)看，這樣的題目做得再多，也無益于提高學(xué)生的綜合能力.所以，我們?cè)谶M(jìn)行數(shù)學(xué)題目的講解教學(xué)時(shí)，為了有效地提高學(xué)生的解題技巧和反應(yīng)速度，都會(huì)增加一些變形題.變形題就是在標(biāo)準(zhǔn)題型的命題基礎(chǔ)上進(jìn)行拓展和延伸，將知識(shí)點(diǎn)進(jìn)行有效的隱藏或轉(zhuǎn)化，讓學(xué)生們?cè)诮忸}過程中不能一眼就看出用哪個(gè)公式或適用于哪條定理.要求學(xué)生對(duì)題目的整體意義和基礎(chǔ)知識(shí)有較高水平的把握，在一定基礎(chǔ)理論的指引之下對(duì)題目進(jìn)行有計(jì)劃、有目的的總結(jié)，然后進(jìn)行合理的轉(zhuǎn)化，在不改變?cè)瓉砻}考核意義的同時(shí)，讓問題得到更簡(jiǎn)便的解決方法.

例如：學(xué)習(xí)了韋達(dá)定理之后，為了考查學(xué)生對(duì)這個(gè)定理的理解和應(yīng)用能力，我設(shè)計(jì)了對(duì)應(yīng)的練習(xí)題，其中有一個(gè)題目是這樣的：

已知a，b是方程x2-x-1=0的根，求a4+3b的值.若要求出a、b的值按常規(guī)方法是很復(fù)雜的，在推導(dǎo)的過程中也容易在不同的環(huán)節(jié)出現(xiàn)錯(cuò)誤.這時(shí)我們就可以通過變形的技巧解答，打破常規(guī)的先從已知條件開始解題的思路，先從結(jié)論出發(fā)，過程如下：

解因?yàn)閍是方程x2-x-1=0的根，那么，a2-a-1=0,a2=a+1.

則a4=(a+1)2=a2+2a+1=a+1+2a+1=3a+2.

因此，a4+3b=3a+2+3b=3(a+b)+2.又∵a,b是方程x2-x-1=0的兩個(gè)根,∴a+b=1,∴a4+3b=5.

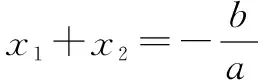
二、通過變形技巧的學(xué)習(xí)，提高學(xué)生的邏輯思維能力

高中階段的三角函數(shù)部分，無論在占比上還是難度上都是一個(gè)大角色，在一些求值、 化簡(jiǎn)、 證明以及解三角方程甚至是解幾何問題等方面都有廣泛的應(yīng)用.在高中數(shù)學(xué)中它都算得上解題工具.但是由于三角函數(shù)部分公式眾多，應(yīng)用于實(shí)際解題中方法是多種多樣的，簡(jiǎn)單的記憶和公式的套用在解決問題的過程中會(huì)讓知識(shí)的應(yīng)用顯得捉襟見肘.如果學(xué)生們能熟練掌握三角恒等變換的技巧，就相當(dāng)于變相地進(jìn)行公式的記憶，同時(shí)還能對(duì)各內(nèi)容之間的聯(lián)系加深理解，促進(jìn)邏輯思維能力的發(fā)展.

例如：已知θ同時(shí)滿足asec2θ-bcosθ=2a和bcos2θ-asecθ=2b,且a、b均為不0，求a、b的關(guān)系.

顯然有：cosθ≠0.

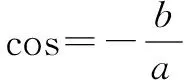
評(píng)析這道例題是“化弦”方法的一個(gè)具體的運(yùn)用，在含同角的三角函數(shù)式的問題中利用的是切割弦之間的基本關(guān)系式，這些關(guān)系式在學(xué)生的大腦中一般是獨(dú)立存在的，他們更善于對(duì)于問題的各個(gè)擊破.在本題中，通過“正余互化”、“切割化弦”等方法減少了函數(shù)的種類，也就是變換了函數(shù)的名稱，是函數(shù)實(shí)質(zhì)的統(tǒng)一思想.這樣有利于找到解決問題的途徑.這樣的變形技巧，要求學(xué)生必須對(duì)高中數(shù)學(xué)中相關(guān)的基礎(chǔ)知識(shí)都心中有數(shù)，將各知識(shí)點(diǎn)進(jìn)行有效的銜接和融合，長(zhǎng)期有目的的練習(xí)會(huì)讓學(xué)生的邏輯思維能力得到有效的提高.

三、通過學(xué)習(xí)變形技巧，培養(yǎng)學(xué)生良好的學(xué)習(xí)習(xí)慣

現(xiàn)在的高中生解決問題有很多的途徑.在信息化的今天，要想獲得一個(gè)問題的答案有很多途徑，好多學(xué)生已經(jīng)習(xí)慣了依賴各種輔助工具學(xué)習(xí)，這實(shí)際是一個(gè)非常不好的現(xiàn)象.在對(duì)變形技巧研究的過程中，我發(fā)現(xiàn)這是一個(gè)很好的讓學(xué)生主動(dòng)學(xué)習(xí)的方法.因?yàn)椋冃晤愒囶}的解題思路是多角度、放射性的，它沒有一個(gè)固定的模式可以遵循，這就給了學(xué)生們很廣闊的想象和實(shí)踐空間.在這個(gè)空間里，學(xué)生可以自由的發(fā)揮，達(dá)成自己的目標(biāo).這個(gè)過程要靠學(xué)生自己獨(dú)立的思維，別人的建議只起輔助作用，長(zhǎng)此他們會(huì)形成良好的自主學(xué)習(xí)習(xí)慣.

通過以上幾點(diǎn)的介紹，主要是為了展示變形技巧在實(shí)際教學(xué)中的應(yīng)用效果.對(duì)于解答問題來說這它是一種方法，而對(duì)于一個(gè)學(xué)生長(zhǎng)遠(yuǎn)的發(fā)展來說它更是一種能力.即是能力就需在實(shí)踐中不斷的改進(jìn)和創(chuàng)新，這樣才能達(dá)到一個(gè)更好的靈活運(yùn)用和綜合提高的效果.