收縮法和PR算法在加權復雜網絡節點重要性評估中的比較

程 晨，李 賀

（1.貴州財經大學 馬克思主義學院，貴陽 550004；2.國家行政學院 經濟學部，北京 100089）

0 引言

復雜網絡（Complex Network），是具有自組織、自相似特性的冪律的度分布概念，是現代商業發展的重要系統論基礎。如商業倫理研究的就是商業與社會的復雜網絡關系，其核心是商業活動中人與人的倫理關系。良性商業倫理關系能夠促進經濟循環增長，但近來年，一些因利益原因出現的賄賂、背叛、悔約等現象，嚴重破壞商業倫理的理想秩序，給經濟和社會帶來一系列的負面影響[1]，因此，商業倫理的抗毀壞性研究在市場經濟領域成為焦點。但以何種方法進行定量研究則爭執不一，魏赟鵬[2]將商譽價值設定為商業倫理指標變量，利用成本計量方法試圖論證商業倫理在商業決策中的作用。該方法能夠為商業倫理在商業決策中提供參考指標，但存在兩點缺陷，一是無法提前估算商譽未來價值，二是無法對商譽成本做出正確的計量估算。肖岳峰[3]從核算模型角度進行商業倫理數理核算，計算出商業倫理作用系數和強度系數。該方法結構明確，而且結果以定量數值方式表示，較為合理。但計算過程中存在層次結構模型，專家評分主觀因素較多，對模型定量數值存在一定影響。

目前學術缺陷和研究不足，造成商業倫理重要性程度評定研究并不完善。實際上商業倫理是一種人際關系模式，符合復雜網絡定義中自組織、自相似、吸引子、小世界、無標度等特征，是典型的復雜網絡小世界。因此將商業倫理納入復雜網絡研究范疇，構建商業倫理復雜網絡。復雜網絡研究中節點重要性評估方法相對成熟，對商業倫理復雜網絡節點重要性評估具有重要借鑒意義。本文以收縮法和PageRank算法為研究工具，對評估過程和計算結果進行對比，以確定最佳研究方法。

1 加權商業倫理復雜網絡

商業倫理網絡作為人際關系的特例，是一種具備動力學行為和復雜拓撲結構的規模性網絡，符合復雜網絡的基本定性。但傳統的無權復雜網絡研究方法主要持統計學及物理學方法，僅定性商業倫理網絡中人際關系的幾何性質和形成結構，只認定商業倫理復雜網絡中的節點是否存在相互作用，忽略商業倫理復雜網絡并不是一個簡單的布爾網絡，各節點之間的相互作用因多種因素存在強度差異[4]，如商業倫理中親情關系、利益因素等。因此在無權復雜網絡基礎上引入加權復雜網絡，形成加權后的商業倫理復雜網絡。實際上引入復雜網絡并不簡單，需對商業倫理復雜網絡中的邊權進行賦值，以反應商業倫理復雜網絡中各節點間的作用強度。一般邊權賦值采用物理權重和抽象權重兩種指標作用參考指標，取二者綜合值作為最終邊權值[5]。而在處理權重關系時一般采用相異或相似原則，相異原則一般表示商業倫理復雜網絡中的空間分布，如商業倫理中二個個體居住距離，相居較遠則權值越大，二節點關系越疏遠。相似原則相反，一般表示商業倫理復雜網絡中主觀因素，如商業倫理中二個個體為戰友關系，則權值越大，二節點的關系越親密[6]。

下面給加權商業倫理復雜網絡進行基本的定量統計描述。假設商業倫理復雜網絡的集合為G=(V，E)，那么商業倫理復雜網絡中個體即為節點，個體之間聯絡方式或人際關系度為商業倫理復雜網絡權重，即邊權。定義商業倫理復雜網絡中的節點集合為 υ={υ1,υ2,υ3,…υn}，υi(i=1，2，3…)為網絡中的一個節點,邊權集合為e={e1,e2,e3,…en} ，用鄰近矩陣M表示。則有加權商業倫理復雜網絡的節點數n=|υ|，連接邊數m=|e|。一般情況下節點集合υ={υ1,υ2,υ3,…υn} 比較易得到，但加權商業倫理復雜網絡中邊權集合e={e1,e2,e3,…en}由于邊權差異不適用三角形不等式，邊權的節點強度ψ需經特殊處理才可得到。同時考慮加權商業倫理復雜網絡中邊的連接方式存在無向和有向二種，節點強度ψ的計算方式分二種。

第一，無向連接網絡節點強度ψ計算。加權商業倫理復雜網絡無向連接中，鄰近矩陣M為對稱矩陣，那么邊權ω 中ωij=ωji(i，j=1，2，3…) 。如果節點之間由邊 ωig和ωgj相連，那么，當兩節點相異時，則節點之間的距離Lij=ωig+ωgj，當兩節點相似時，則節點之間的距離。最終節點之間的平均距離為：L=，在此基礎上，得到無向連接下加權商業倫理復雜網絡中節點強度

第二，有向連接網絡節點強度ψ計算。加權商業倫理復雜網絡有向連接中，節點強度分為入強度ψin和出強度ψοut。假設二節點υi，υj由二條有向邊相接，二條邊的邊權值分別為，那么入強度為指向節點υi的集合，出強度為節點 υi的指向集合）。

理論顯示，在加權商業倫理復雜網絡中的節點強度存在顯著差異，節點強度具有網絡抗毀性，如果5%的核心節點被侵占，則某個加權后的商業倫理復雜網絡有可能進入無序狀態，甚至使整個商業倫理網絡陷入混亂[7]，因此對加權后的商業倫理復雜網絡進行節點重要性評估成為重點。依據傳統理論，分析節點強度ψ可排序加權商業倫理復雜網絡的節點重要性，但該方法排序過程中忽視橋節點，排序結果較為片面。而以節點間的最短路徑幾率作為排序標準，則由于模型的復雜程度較高，排序結果容易出現計算錯誤。

2 收縮法的加權商業倫理復雜網絡節點重要性評估

收縮法的核心思想是將加權商業倫理復雜網絡中節點υi與鄰近相連的節點結合，形成新的節點，之前與節點υi相連的邊重新與節點相連。收縮后的節點與加權商業倫理復雜網絡凝聚在一起，一般用網絡凝聚程度?(g)表示新節點的重要度，數值為節點數n與平均路徑長度L的乘積倒數[8]。即：

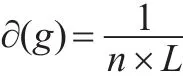
進一步優化后：

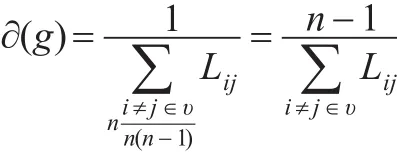
其中Lij表示二節點最短距離，n≥2。那么收縮后加權商業倫理復雜網絡中的節點重要度為：

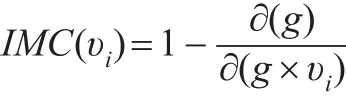
綜上述，收縮法對加權商業倫理復雜網絡節點重要性評估綜合了節點數目及節點連接邊權，如果節點υi的鄰接節點數目越少，位置越重要，則收縮后的節點網絡凝聚程度越高，顯然有悖常理。

2.1 優化網絡凝聚程度?(G)

前述收縮法借鑒無權復雜網絡構建加權商業倫理復雜網絡的網絡凝聚程度，忽略了加權商業倫理復雜網絡存在邊權差異，節點數n與平均路徑長度L的乘積倒數并不能完全表示收縮后加權商業倫理復雜網絡的凝聚度。因此前述網絡凝聚程度?(g)值并不能直接使用，需要從加權商業倫理復雜網絡維度進行優化，并將時間復雜度納入考察范圍。假設存在加權商業倫理復雜網絡G=(V，E)，該網絡各節點之間相互獨立，連接邊數少于或等于1，邊權相異且ω∈(1,+∞)。那么對該網絡進行優化收縮，首先將節點υi與鄰近節點關聯形成新節點υi'，邊權為收縮圈邊緣的邊權值，如圖1所示：

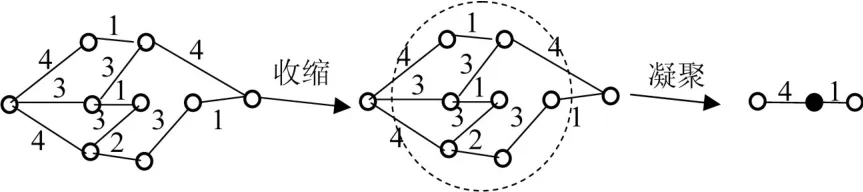
圖1 節點收縮示意圖

然后計算收縮后的網絡凝聚度?(G)，此時需要考慮邊權差異，用平均點權之和s與退化為無權商業倫理復雜網絡后的網絡平均距離l乘積倒數表示，目的在于避免邊權差異和路由變化對收縮后計算結果造成影響，即：

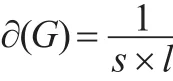
進一步優化后：

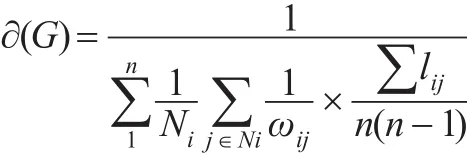
其中lij表示二節點加權路由路徑下的無權最短距離，n≥2。那么優化收縮后加權商業倫理復雜網絡中的節點重要度為：

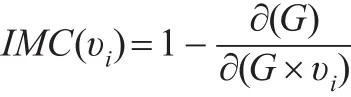
從優化后的收縮加權商業倫理復雜網絡節點重要度公式來看，節點重要度主要取決于節點網絡位置和節點連接數。如果節點處于網絡關鍵位置，最短路徑越少，收縮后平均距離lij變化越大，那么網絡凝聚度?(G)值越大。如果節點連接數目越多聯系越緊密,收縮后節點的點權均值和數目越少,那么網絡凝聚度?(G)值越大。

2.2 節點重要性程度評估算法改進

收縮法與節點間最短路徑評估方法類似，即采用節點間最短距離的線性關系進行復雜度優化計算。但由于加權商業倫理復雜網絡需采用Floyd循環算法，導致整個計算過程時間復雜度超過無權復雜網絡，由O(n3)變成了O(n4)，故需對加權商業倫理復雜網絡節點重要性程度評估計算過程進行改進。根據前述網絡凝聚程度思路，除計算加權商業倫理復雜網絡中的平均點權之和s和退化為無權商業倫理復雜網絡后的網絡平均距離l外，繼續引入節點連邊的重要度計算。假設加權商業倫理復雜網絡G=(V，E)的邊為節點，而網絡中的各邊由邊連接，那么即可將網絡G=(V，E)收縮為G=(V，E)'，利用優化后網絡凝聚程度的計算方法重新評估網絡G=(V，E)'節點重要度，疊加網絡G=(V，E)與網絡G=(V，E)'的節點重要度。其計算公式如下：

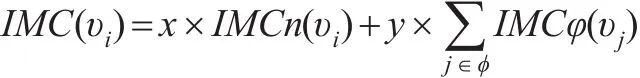
式中 φ 為節點集合，IMC(υi)和 IMCφ(υj)分別表示網絡G=(V，E)和G=(V，E)'中對應節點υi的節點重要度和連邊節點重要度，考慮網絡為加權網絡，用x、y分別表示節點重要度和連邊重要度的加權系數。為便于理解，使用改進算法后的節點連邊示意圖進行說明，見圖2。

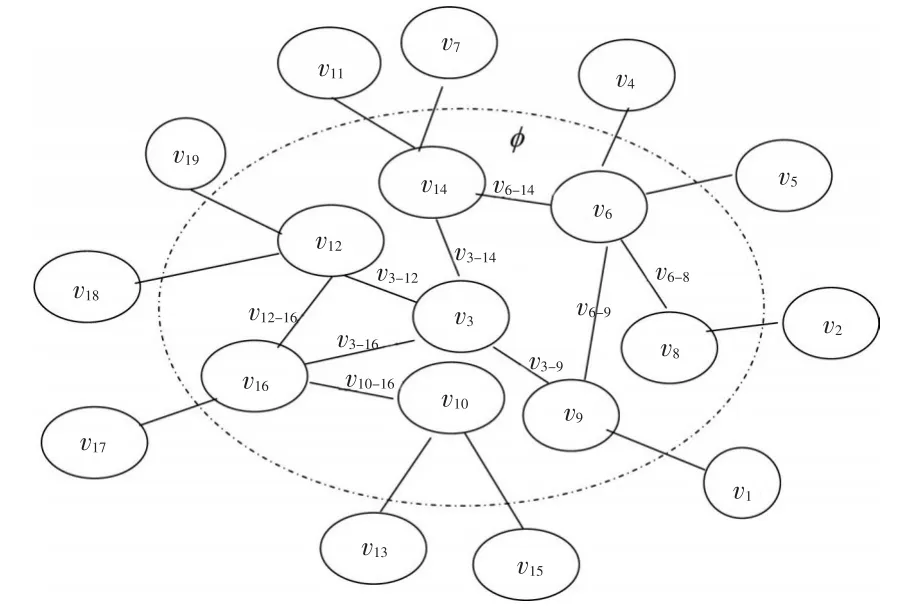
圖2 改進算法后的節點連邊圖

從計算公式和示意圖可見，改進算法后的收縮法，節點重要性評估取決于節點數目、節點位置、節點連邊重要度及節點重要度和連邊重要度的加權系數x、y，相對而言，該收縮法屬于較為全面的研究方式。但同時存在計算結果大于1（即IMC(υi)＞1）的情況，因此需要對節點重要度 IMC(υi)的計算結果進行歸一化處理，用 IMCf(υi)表示，歸一化處理結果如下：

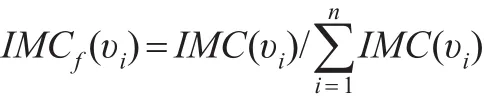
總結改進收縮法的計算過程發現，收縮法計算商業倫理復雜網絡節點重要度的核心思想還是網絡凝聚程度，只是收縮法在網絡凝聚程度基礎上，將變量因素從節點數和平均路徑長度擴展到平均點權之和、網絡平均距離和節點連邊的重要度。盡管收縮法中間計算過程將時間復雜度由O(n)3變成O(n)4，但通過改進收縮法后時間復雜度為O(n)3，整個算法的復雜度為O(n)3，對于加權商業倫理復雜網絡節點重要度的計算較為理想。

3 PageRank算法的加權商業倫理復雜網絡節點重要性評估

3.1 PageRank算法

PageRank算法由Google搜索發展而來，最初是為解釋Google搜索引擎中網頁排名問題，依據某網頁如被更多網頁鏈接，則認定某網頁的排名度更高[9]。因此PageRank算法實際是體現網頁之間的相對鏈接關系，如圖1中①→②表示網頁①中有鏈接鏈向網頁②，則說明①為網頁②貢獻了PageRank值。圖3共示意了7個網頁的鏈接關系。

可以看出PageRank算法中的網頁權重關系，由鏈向某網頁的鏈接數量投票決定，網頁被鏈向則意味權重值增加，網頁最終權重值為鏈向該網頁的權重值之和，用公式表示如下：

式中 PR(α)為網頁 α 的PageRank值，PR(β)、PR(x)、PR(δ)…則表示網頁 β 、x、δ…鏈向網頁 α 的PageRank值，而C(β)、C(x)、C(δ)…分別表示網頁 β 、x、δ…鏈向其他網頁的數量,因此可得出網頁α的PageRank值矩陣,其中αmn=PR(n)/c(n)。

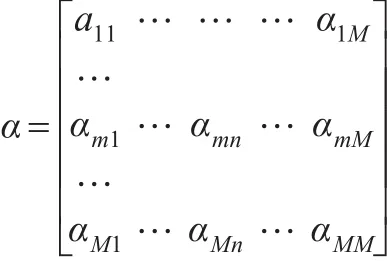
由網頁α的PageRank值矩陣可知，如果某網頁存在鏈向其他網頁鏈接，則證明該網頁對其他網頁貢獻了PageRank值，但該網頁貢獻的PageRank值大小取決于該網頁的重要程度，網頁越重要其貢獻的PageRank值越大。上述結論的基礎是網頁鏈向是單向鏈接，由于實際網頁鏈接存在雙向鏈接，故網頁的PageRank值計算屬于一個迭代過程。假設向量 β(β1，β2，β3，…，βn)（其中 β0=(1，1，1…，1)）為網頁的PageRank值排序，那么網頁PageRank值的第i次迭代結果為：

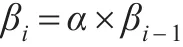
理論表明βi存在收斂現象，而且網頁之間的鏈接關系屬于概率事件，存在概率為0或1的可能，故對迭代結果進行平滑處理，引入平滑處理因子?=0.85，單位矩陣用?表示，網頁數量用n表示，結果如下：

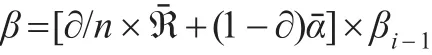
通過上述處理后，如果假設條件為網頁的初始權重值為1，那么可得到圖1網頁鏈接關系的PageRank值矩陣。

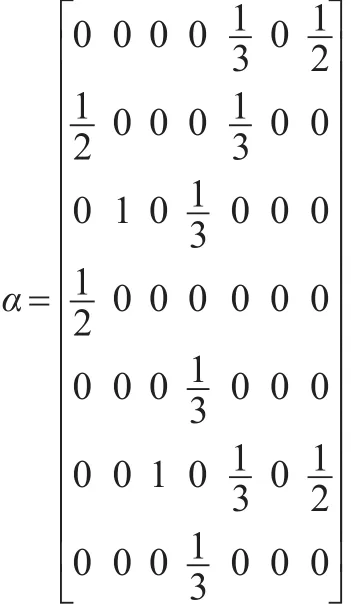
顯然，PageRank排序算法能夠準確的將網頁重要程度進行排列，并且具有可靠性。對比網頁的PageRank排序算法發現，實際上商業倫理網絡各節點之間的聯系就是一個類似網頁鏈接關系，商業倫理網絡節點之間是否關聯，節點的重要性程度如何，亦可用類似節點之間是否存在“鏈接”表示。因此PageRank排序算法對商業倫理復雜網絡節點重要程度的排序具有重要的借鑒意義，接下來借鑒PageRank排序算法對加權商業倫理復雜網絡中的節點重要程度進行演算。

3.2 Page Rank算法與加權復雜網絡的結合

既然引入PageRank算法，那么對商業倫理加權復雜網絡的節點重要性重新定義評估指標WG-PageRank。但上述PageRank算法存在缺陷，PageRank算法考慮了網頁鏈接中的迭代現象，卻將網頁中的初始權重值全部定義為1。商業倫理復雜網絡中由于各節點中的關系影響（如親人、同學等），導致各節點中的初始權重值并不相同，因此在商業倫理加權復雜網絡中并不能將各節點初始權重值定義為1。故需對PageRank算法進行優化。假定在加權商業倫理復雜網絡中有n個節點，其中節點υ與節點υ1、υ2、υ3、...υi相連，同時節點 υi對節點 υ的權重為 ω(υi,υ)，那么可定節點υ的重要性評估指標WG-PageRank如下：

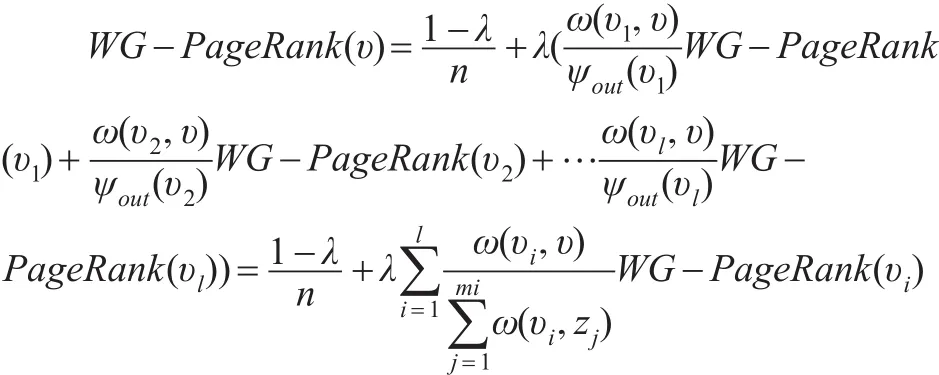
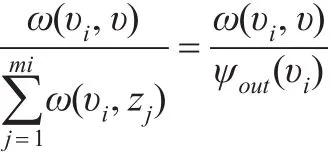
通過上述方法后，解決了網頁PageRank算法中無法給不同節點賦值的缺陷，使之更加符合加權商業倫理復雜網絡節點重要性評估運算的需要。

3.3 節點重要性程度評估

根據前述理論，商業倫理網絡屬于加權復雜網絡范疇，定加權商業倫理復雜網絡為G=(V，E),為對其重要性進行評估，首先找出鄰接矩陣M，用矩陣M來表示網絡G中n個節點的鏈接關系。

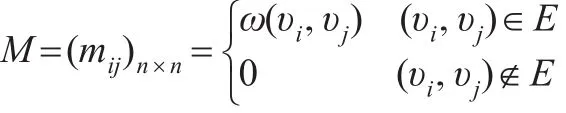
從鄰接矩陣可以看出，加權商業倫理復雜網絡中各節點的鏈接關系存在兩種形式，即當兩節點之間相鏈時，那么鄰接矩陣M中的數值即為兩節點的權重值，否則表示兩節點之間不相鏈，矩陣M中的數值為0。考慮到一些封閉商業形式（如軍事、保密行業等），商業倫理復雜網絡中的節點并不向外鏈接，計算后鄰接矩陣M中某行值全部為0，則稱該節點為懸虛節點。另外，商業倫理復雜網絡中的節點是否相鏈還是一個概率事件，因此還需要對鄰接矩陣進行概率歸一化處理，以記錄矩陣M中各節點與另外節點接鏈的概率。處理公式如下：

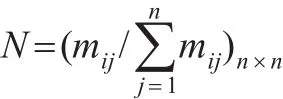
通過上述公式計算后，得到新矩陣N，即為概率轉移矩陣。概率轉移矩陣N中同樣存在鄰接矩陣M中的懸虛節點，為便于計算，用向量（1/n）eT置換概率轉移矩陣N中全部為0的行，即可得到懸虛節點概率轉移矩陣N'：

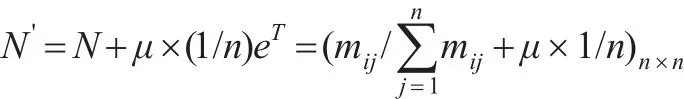
其中式中μ為一個二進制數字，用于判斷某節點是否為懸虛節點，當節點為懸虛節點時，μ取值為1，否則為0。得到懸虛節點概率轉移矩陣N'后，便可計算網絡G的WG-PageRank值的矩陣α。由于每個節點與其他節點的鏈接一般存在阻尼，故引入阻尼系數λ，而且商業倫理復雜網絡中主要分析鏈入關系，需要使用概率轉移矩陣N'的轉置矩陣N'T，得到結果如下：

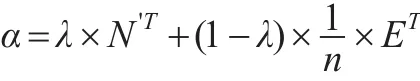
當矩陣中某行的數值全部為1時，ET=e×eT。計算后得到加權商業倫理復雜網絡重要性矩陣α后，然后對節點重要性進行排序即可。總結PageRank算法在加權商業倫理復雜網絡節點重要性評估中的運用后發現，該方法的時間復雜度為O(n2)，空間復雜度為O(n2)。

4 兩種方法的實驗對比

為驗證改進收縮法和PageRank算法在加權商業倫理復雜網絡節點重要性評估計算中的有效性，選擇某沿海城市13家小型企業（相互之間存在關聯）為研究對象，節點選擇企業董事長，連接邊以企業董事長2017年12月內是否通話為依據，連接邊的權值即為2017年12月的通知次數，通過處理分析即可得到該加權商業倫理復雜網絡的拓撲結構，如圖4所示。

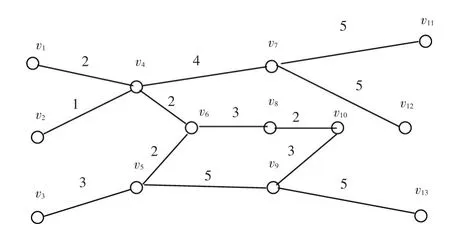
圖4 某加權商業倫理復雜網絡的樹形拓撲結構

4.1 排序結果比較

利用本文提出的改進收縮法和PageRank算法估計該加權商業倫理復雜網絡的節點重要度。考慮市場公平原則，定該網絡中的節點為平等的合作關系，則收縮法中節點重要度和連邊重要度的加權系數x=y=0.5。而PageRank算法中，阻尼系數λ數值大小能夠體現節點相對重要度和決定算法迭代收斂速度，故將阻尼系數λ設置為合理的0.85，兼顧二者之間的平衡。設定加權系數和阻尼系數后，依據收縮法和PageRank算法，則可得到具體的評估結果和排序結果，見表1。

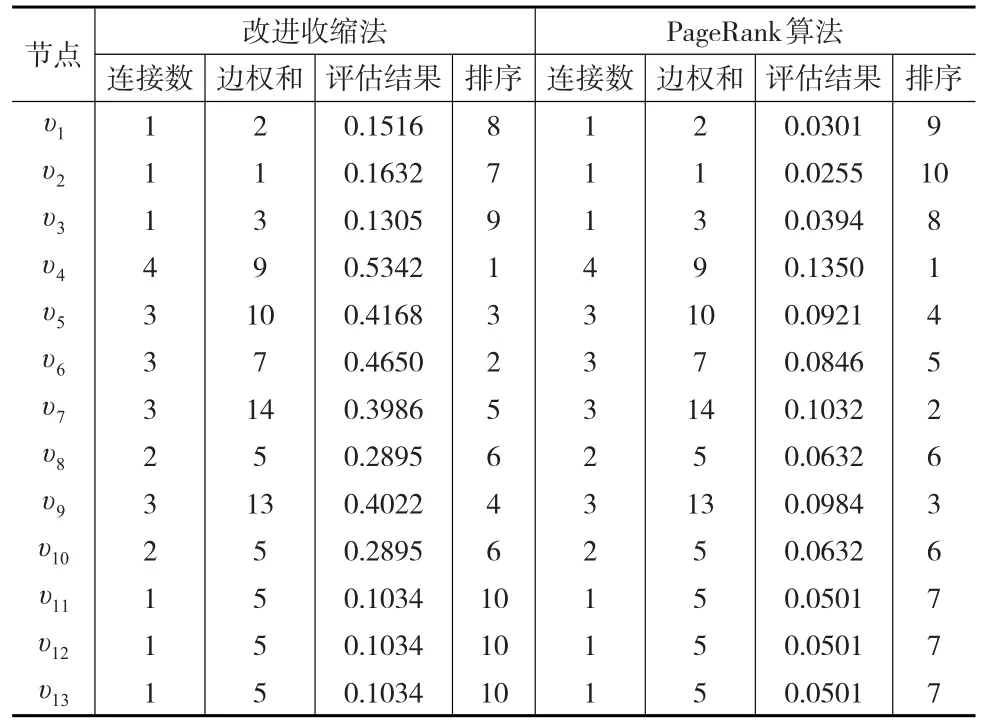
表1 改進收縮法和PageRank算法的節點重要度評估結果

從結果看，改進收縮法和PageRank算法的排序結果略有差異，改進收縮法排序結果為 υ4＞υ6＞υ5＞υ9＞υ7＞υ8=υ10＞υ2＞υ1＞υ3＞υ11=υ12=υ13，而 PageRank算法排序結果為 υ4＞υ7＞υ9＞υ5＞υ6＞υ8=υ10＞υ11=υ12=υ13＞υ3＞υ1＞υ2。其中節點υ4無論是改進收縮法還是PageRank算法，都處在該加權商業倫理復雜網絡的關鍵位置，說明改進收縮法和PageRank算法對加權商業倫理復雜網絡節點重要性評估的核心觀點一致。區別在于PageRank算法相對改進收縮算法節點 υ7和 υ6、υ9和 υ5、（υ11、υ12、υ13）和 υ2、υ3和υ1的排序位置進行了更換，原因可能是由于PageR-ank算法考慮了節點連接邊的方向性，對節點重要性的評估計算中考慮了入強度ψin和出強度ψοut。而改進收縮法偏向節點連接數目，節點重要度IMC(υi)的計算結果又進行過歸一化處理，故其計算數值可能更接近節點重要度實際值，但排序結果可能與理論值有一定的偏差。由此可見改進收縮法和PageRank算法在加權商業倫理復雜網絡節點重要性評估中各有千秋，但由于改進收縮法的排序結果更接近實際值，條件許可下，本文更偏向采用改進收縮法對加權商業倫理復雜網絡的節點重要性進行評估。

4.2 運行時間比較

考慮時間成本，利用隨機模型建立隨機加權商業倫理復雜網絡，分別采用改進收縮法和PageRank算法對隨機網絡中的節點進行重要性評估，通過多次運行得出運行時間的平均值，結果見圖5。

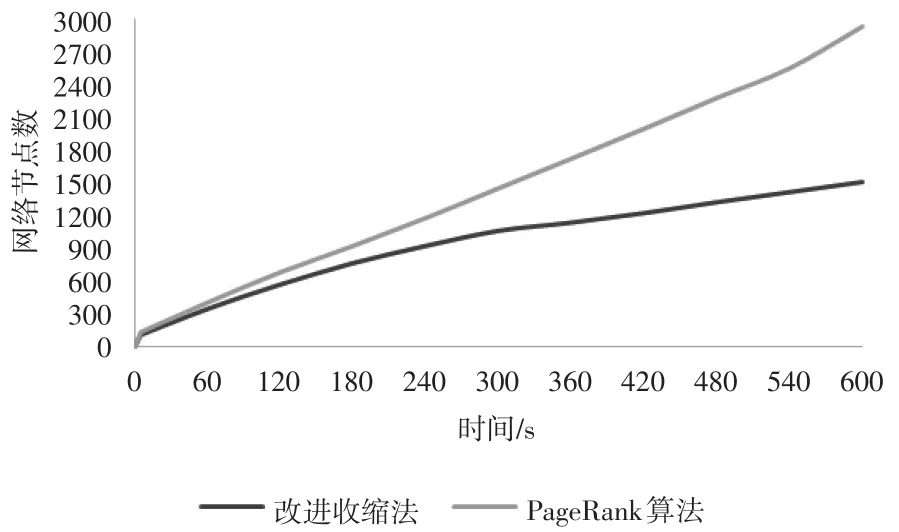
圖5 不同算法和不同節點數目的運行時間

從圖5可以看出，當加權商業倫理復雜網絡中節點數目少于100時，改進收縮法和PageRank算法的運行時間基本控制在5s以內，而隨著加權商業倫理復雜網絡節點數目的增加，改進收縮法的運行時間明顯長于PageRank算法，原因是由于改進收縮法需要消耗大量時間來計算平均點權之和、網絡平均距離和節點連邊的重要度等多個變量數值。由此可見，當評估小型加權商業倫理復雜網絡節點重要性時，適合選取改進收縮法，而當評估大型加權商業倫理復雜網絡節點重要性時，選取PageRank算法更能在時間上獲得計算優勢。

5 總結

將商業倫理納入復雜網絡研究范疇后發現，如果以傳統無權復雜網絡定義商業倫理復雜網絡，則忽略了商業倫理復雜網絡并不是一個簡單的布爾網絡，各節點之間的相互作用因多種因素原因存在強度差異。因此本文在無權復雜網絡的基礎上引入加權復雜網絡，對商業倫理復雜網絡中的邊權進行賦值，以反應商業倫理復雜網絡中各節點間的作用強度，從而構建加權商業倫理復雜網絡。由于傳統加權商業倫理復雜網絡節點重點性評估方法不完善，本文引入收縮法和PageRank算法，并對二種方法進行實驗對比。結果表明：

（1）改進收縮法計算商業倫理復雜網絡節點重要度的核心思想是網絡凝聚程度，只是改進收縮法在網絡凝聚程度基礎上，將變量因素從節點數和平均路徑長度擴展到平均點權之和、網絡平均距離和節點連邊的重要度，改進收縮法時間復雜度為O(n3)，整個算法的復雜度為O(n3)。

（2）PageRank算法由網頁PageRank算法演變而來，主要以節點之間的鏈向關系為依據，通過計算加權商業倫理復雜網絡重要性矩陣對節點重要性進行排序，PageRank算法的時間復雜度為O(n2)，空間復雜度為O(n2)。

（3）從實驗排序結果來看，改進收縮法的排序結果更接近實際值，PageRank算法接近理論值，在條件許可下，本文偏向采用改進收縮法對加權商業倫理復雜網絡節點重要性進行評估，但對于大型加權商業倫理復雜網絡節點重要性評估中，考慮時間成本條件下，則選擇PageRank算法。