基于TIT2FS幾何度量的LINMAP方法

彭 潁，毛軍軍,1b，張鳳曉，鄒 斌

（1.安徽大學a.數學科學學院；b.計算智能與信號處理教育部重點實驗室；2.安徽廣播電視大學 教育科學學院，合肥 230601）

0 引言

近年來，模糊理論受到研究者的廣泛關注。在模糊的研究中美國控制論專家Zadeh[1]首先提出模糊集合理論，此后研究者在該理論的基礎上更進一步的完善和推廣。首先模糊集是帶有精確定義的隸屬函數或隸屬度，然而在實際中，有時隸屬度仍表現出模糊性，使之很難用一個數值表示，由此提出區間二型模糊集。其次，當人類在描述評價客觀事物時，更慣用語言方式。為了更加貼切人類的正常思維及生活方式，進而不同語言評價值的處理方式日益受到研究者的青睞。

目前語言評價值的處理方法主要有以下3種:將語言信息轉化為模糊數來計算、使用語言下標處理語言信息、將語言轉化為二元語義處理。隨著對模糊集理論的探索與研究，第一種方法更受到廣大研究者與決策者的關注[2-9]，因而衍生出區間梯形二型模糊集，它能夠有效客觀的將語言評估轉變成數字變量。以區間梯形二型模糊向量與其近似正負理想的幾何度量給出擬合指數，再結合區間二型LINMAP方法得到最佳的決策選擇，這樣既簡化計算又合理精確。

1 基本概念

區間二型模糊集的基本概念會廣泛應用于本文中，在這部分會做一個簡短的回顧，從經典模糊集到更具廣泛性的區間二型模糊集以及基于區間二型模糊環境下的區間二型梯形模糊數，它將會用于本文的決策規劃中，是本文探討的根本。

1.1 區間二型模糊集的基本概念

定義1[9]：設X為論域，則定義在X上的二型模糊集A表示[0， 1]}，fx()

u∈[0，1]}。其中Jx表示論域X中元素x對于A的主隸屬函數，u是Jx中的某一個主隸屬函數值；對全部的稱為x關于A的次隸屬函數。

定義2[9]：設A是論域X上的二型模糊集，若對?u∈Jx有，則A稱為論域X上的區間二型模糊集，表示為:。這里μA()x是x對A的主隸屬度。

1.2 決策環境下的區間梯形二型模糊集

區間梯形二型模糊集是區間二型模糊集的特例，考慮多準則決策問題時，本文用區間梯形二型模糊集來表示評估等級。其中定義為決策的m個選擇，讓x1，x2和xn表示c1，c2和cn的相應的數值。集合C可以分成CI和CII兩個集合，CI表示利潤標準，CII表示成本標準，CI∩CII=?，CI∪CII=C。

定義3[10]：對任意非負梯形模糊數Aij(Aij∈[0，1]) ，和μAiU()

x分別為Aij的下隸屬函數和上隸屬函數(xj∈X)，區間二型梯形模糊數Aij表示為：

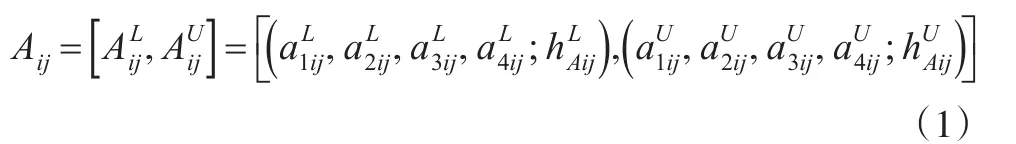
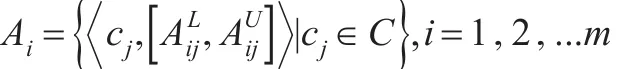
令wj是每個標準cj∈C的權重，其滿足標準化條件，且。設未知的標準C的權重向量為，需要借助后面提出的區間二型模糊LINMAP方法解得。

2 區間梯形二型模糊環境下的不確定性幾何度量

2.1 區間二型梯形模糊向量

區間二型模糊集是區間一型模糊集模糊化的結果，即對一般集合描述事物的再一次模糊化，這是區間二型模糊的鮮明特征。現在考慮是否以向量形式將本文中的區間梯形二型模糊集表示出來，以下給出定義及說明。

定義4：從非負區間梯形二型模糊數Aij中任取兩個模糊數，用Af、Ag表示：

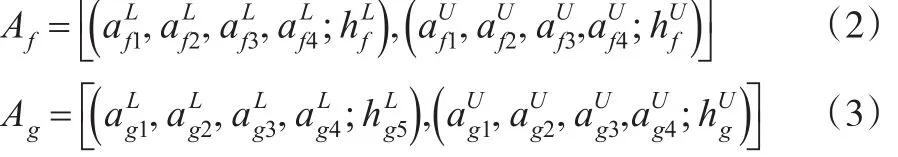
將其化為模糊向量，記為：

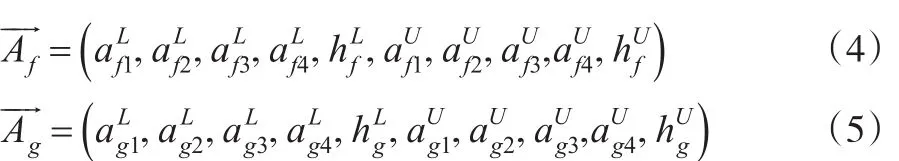
因為區間二型模糊數是對一型模糊數的進一步模糊化，為了保證區間梯形二型模糊數的有效性，區間梯形二型模糊數在轉化為模糊向量時不改變其數值，將其整體視為向量。模糊數中各項均為大于0小于1的數，此證明見文獻[10]。

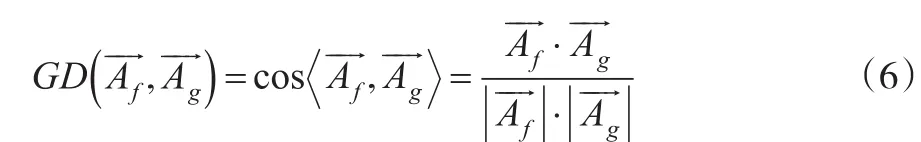
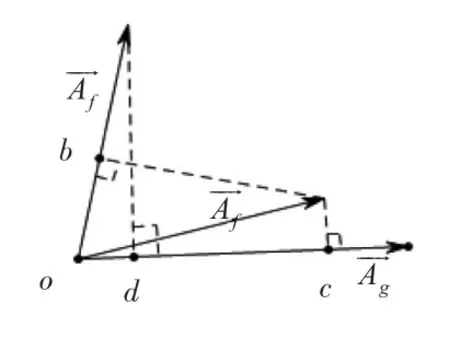
圖1 模糊向量投影

2.2 區間二型梯形模糊向量的近似理想

區間二型梯形模糊向量近似理想的引用，一是為了說明當區間梯形二型模糊數轉化成向量時其幾何夾角問題，二是為了引出本文對區間梯形二型模糊向量給出排序的關鍵。若將正負理想用于區間梯形二型模糊數中，則得到的正負理想并非是區間梯形二型模糊數，因此采用文獻[10]提出的近似正負理想并向量化。

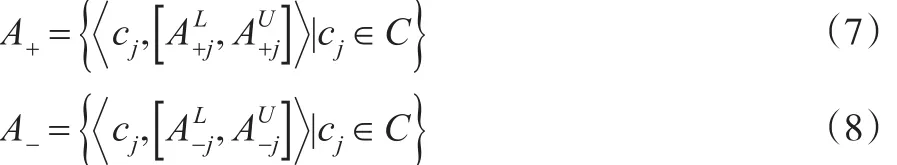
在標準cj∈C下，由式（7）、式（8）得近似正負理想向量和具體表示下：

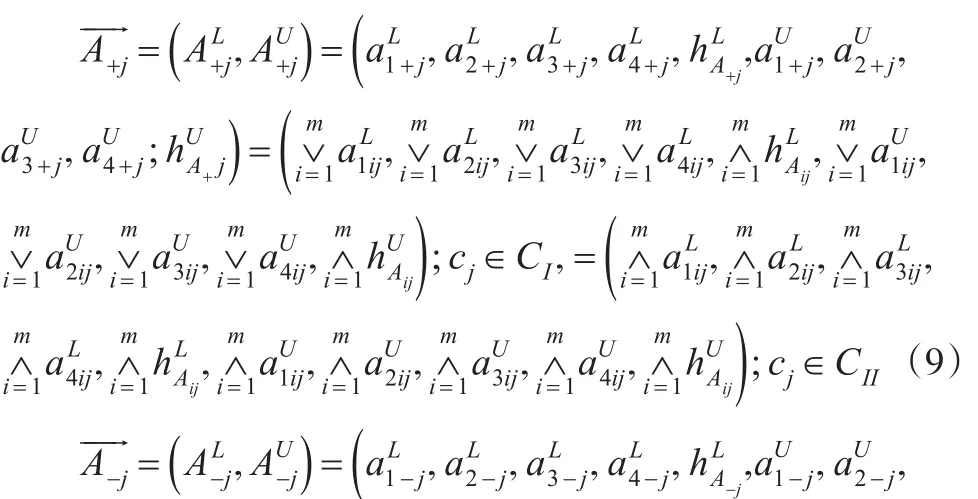
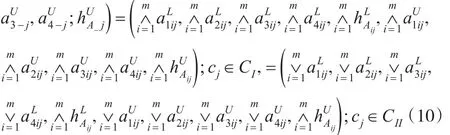
有了二型梯形模糊數的近似正負理想，可以得到在某標準下的近似正負理想的模糊數，由定義5將一組二型梯形模糊數轉化為向量后，可以知道這一組模糊向量的近似正負理想必將這組模糊向量包含其中，因此可以通過近似正負理想的向量得出這組模糊向量的夾角范圍及其性質。

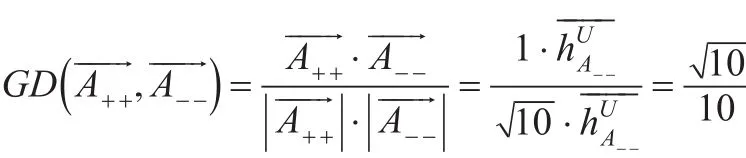
當一組模糊數的近似正負理想向量相等時，此時向量夾角最小為0同時余弦值最大，有

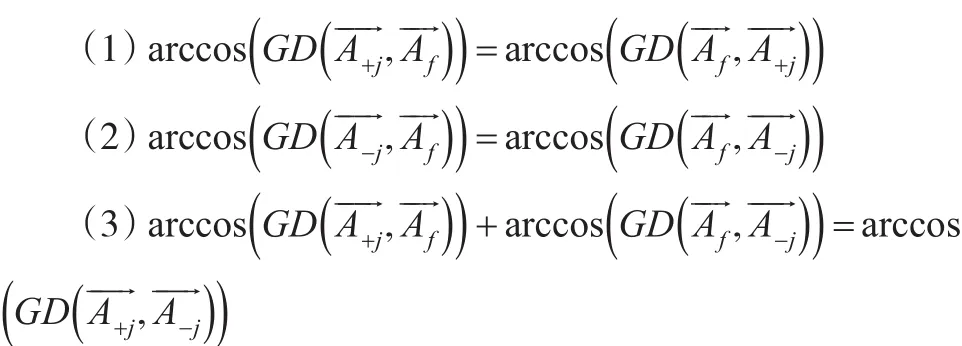
證明：由余弦本身的特征可知（1）、（2）顯然成立；欲證（3）將向量做幾何投影到平面oxy上，依據空間向量投影公式和反余弦函數，（3）顯然成立。

3 區間二型模糊LINMAP方法

3.1 擬合指數

在許多前人研究中，大多使用所選擇方案與其正負理想之間的距離，作為組成貼近度系數的成分。為了得到更為合理精確的貼近度系數，有時會通過計算對不同距離公式進行比較，從而產生大量復雜的運算，如文獻[10]中的閔可夫斯基距離公式。為了區分模糊數的貼近度，本文給出基于區間梯形二型模糊向量的擬合指數，設為非負區間梯形二型模糊向量--Aij，在標準cj下選擇zi的擬合指數公式為：

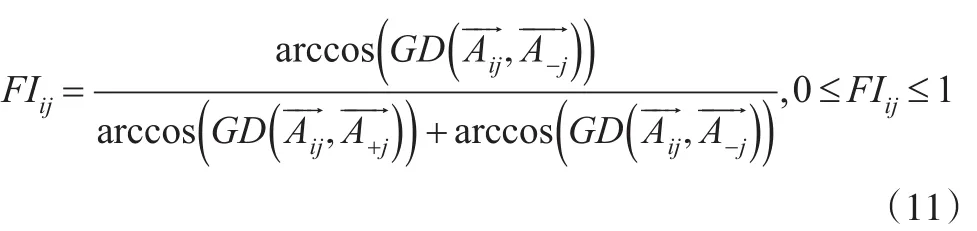
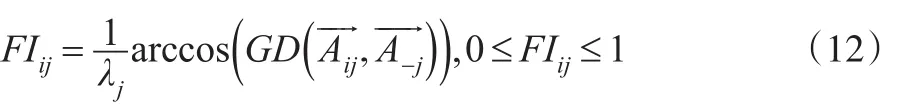
3.2 最優模型

基于區間梯形二型模糊向量解決多準則決策問題的LINMAP方法，文獻[10]給出了區間二型模糊LINMAP方法，基于區間梯形二型模糊向量我們對其作出改進。

定義7：假設Ω為一系列表示選擇方案偏好關系的有序對集合，在標準cj∈C下的未知權重向量是w=(w1，則選擇方案zi∈Z的綜合擬合指數WIi表示為：

上文提到當決策者所表達的偏好排序與計算的排序不一致時，需要盡可能減小這種不一致性。現假設zf偏好于zg，相應的應滿足FIf≥FIg。依照這種規則定義Ω中一致性系數和不一致性系數公式如下：

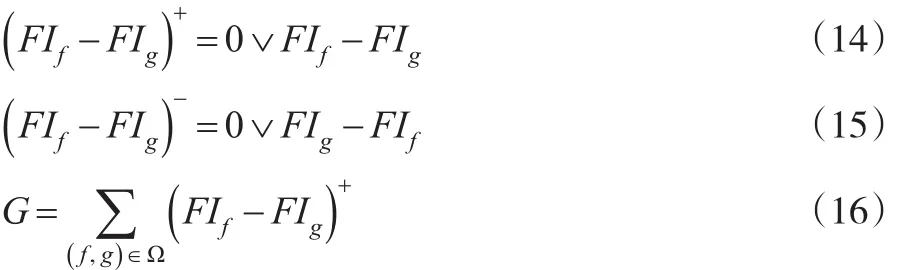
為Ω中所有有序對一致性系數之和;

為Ω中所有有序對不一致性之和;

G-B≥η為決策者最低接受限度，以此建立最優模型，為了使不一致系數B最小，則最優模型構建為:

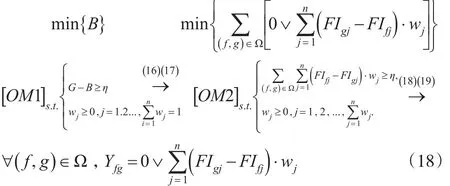
顯然Yfg≥0，即，此時有：

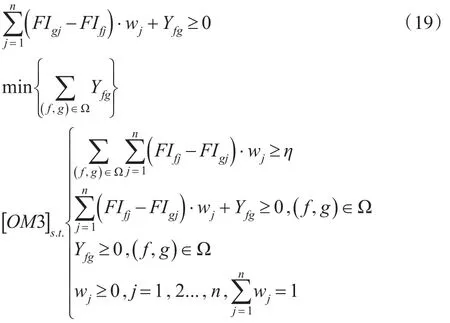
最后，通過區間二型LINMAP方法解出更為合理的最優權重-wj，其綜合擬合指數為：

對?zi∈Z依據對m個選擇項進行排序，從中選擇數值最大的，即為決策者的最佳選擇。

4 算例比較

參考文獻[10]的算例，一個化學藥品和光纖公式的高管，希望選擇合適的供應商，以減小供應鏈的風險和不確定性，最后從中選出5個供應商。

第二步：供應商候選人的語言評估等級（見表1）構建區間梯形二型模糊數Aij，并轉化成區間梯形二型模糊向量。

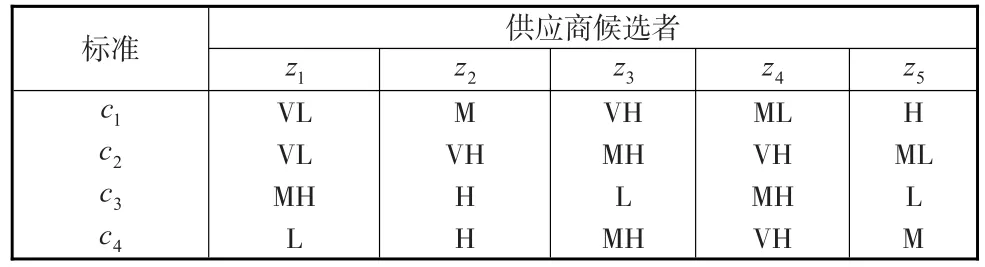
表1 語言評估等級

第三步，假設決策者對這5個供應商提供的成對比較信息為：

第四步，構建標準cj∈C下的近似正負理想模糊向量；計算擬合指數FIij：

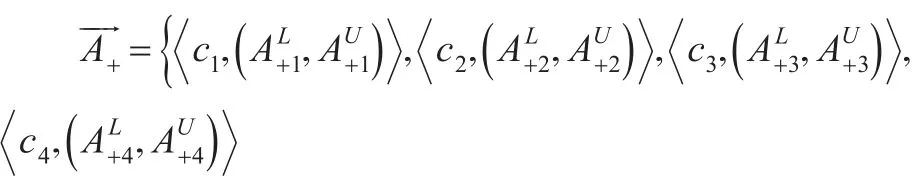
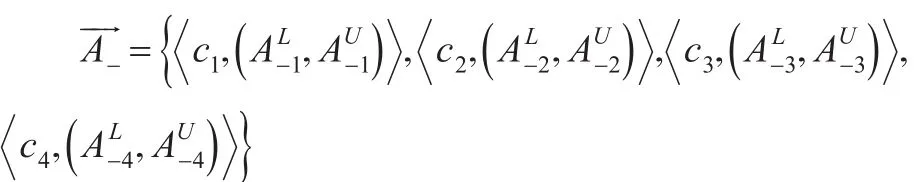
得到近似正負理想的區間梯形二型模糊向量。應用式（11）將基于上面所求得的模糊向量做擬合指數的計算。如表2所示。

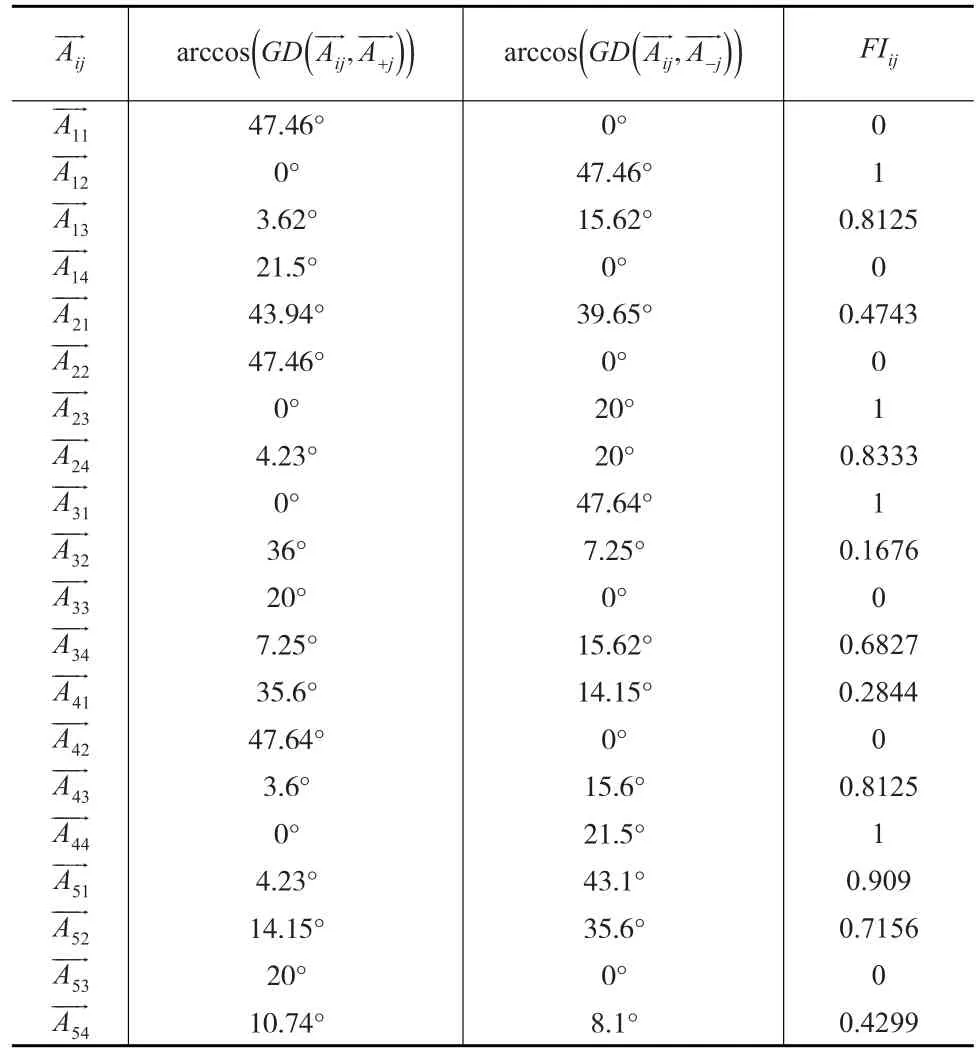
表2 擬合指數

第五步，假設決策者可接受最低限度η=0.3，w=(w1，w2，...，wn)為未知權重，滿足wj≥0，j=1，2，3，4 ，序對 Ω=，應用線性規劃模型，得：

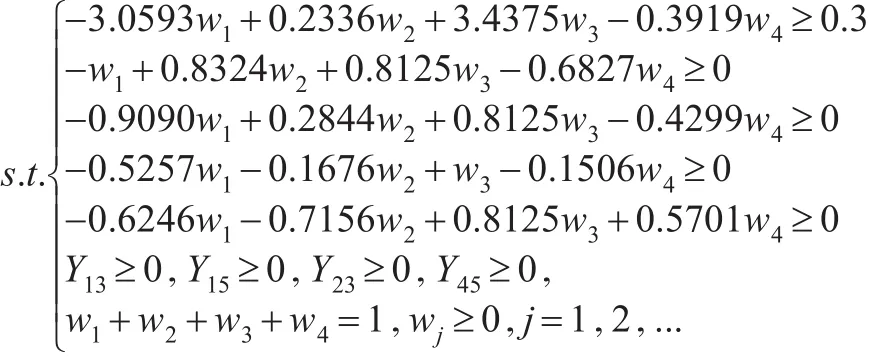
第六步，應用解得的wˉ，應用式（15）計算綜合擬合指數如下：

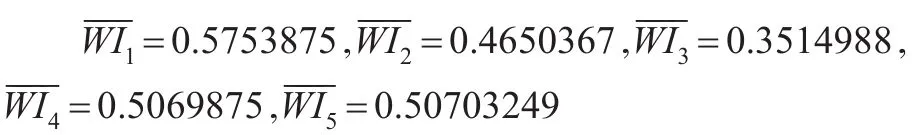
5 結論

本文給出了區間梯形二型模糊向量的定義，及相關性質的證明。在此基礎上引出模糊向量的近似正負理想，利用區間梯形二型模糊向量與其近似正負理想之間的夾角關系，提出擬合指數和綜合擬合指數。以往選擇距離公式計算擬合指數，有時需要比較哪種距離公式更為合理精確，增加了計算量和復雜程度。本文提出的擬合指數公式簡化復雜的運算，同時保證了其結果的合理精確性。最后使用區間二型LINMAP方法，對方案進行排序得到最優方案。