從一道題談解題教學中邏輯結構的構建

江蘇省蘇州陽山實驗學校 (215151)

袁琴琴

解題信息論認為，數學解題的過程，就是數學問題信息的獲取、存儲、處理、輸出，從而實現解題目標的活動過程.羅增儒教授則將數學解題過程總結為“三位一體”的工作：有用捕捉、有關提取、有效組合.為了真正意義上達到以上工作，首先要正確表征已有信息，而表征過程中較為適用的方式就是通過啟發性提示語確定思維起點，進而與記憶儲存中相關定理、公式、及其推理過程、基本模式(模型)等解題依據進行深度整合，形成解題時有效的邏輯結構.于是，捕捉信息與提取依據是形成邏輯結構的基礎，是推進問題解決的源動力.在解題教學中若能展示邏輯結構的形成過程，則有可能對學生解題中的思維過程和心理過程進行恰當的分析，合理的調控，對培養學生的思維品質和心理表征能力有一定的幫助.本文試借一題談談對此的認識.

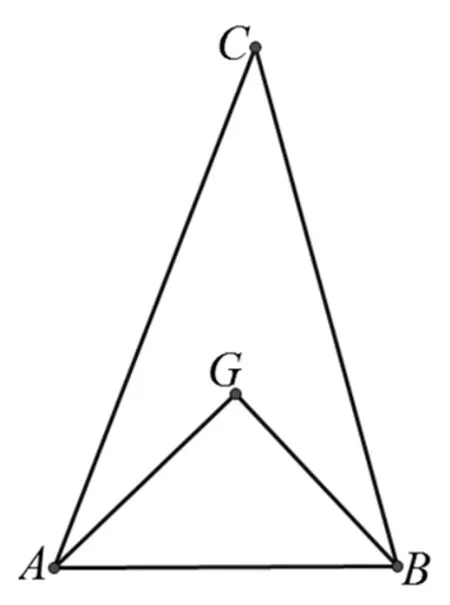
圖1

看下面一道題：如圖1，若點G為ΔABC的重心，且AG⊥BG，則sinC的最大值為 .

1.分析提示語，形成合理的思維方向

學生的知識結構和解題經驗的個體差異，直接導致對已有信息產生強弱不一的心理刺激，即在已有認知“元”的調配下產生了最先“提示語”的自我認知，以自己熟悉(或熟練)的觀點和方式作為思維活動的起點，并嘗試調動已有認知動力，逐步揭開問題中各個未知信息.因此，我們應教學生捕捉到已有信息(包括條件與結論)中的“提示語”，通過對“提示語”的加工、解釋、轉換等方式，啟發出正確的思維起點.

捕捉信息：問題中含有兩個基本提示語——“重心”和“垂直”.

提示語分析：可以發現，這兩個信息的最初表征與學生的元認知密切有關，不同的知識基礎對信息理解的深度不一，進而產生不同的思維起點.

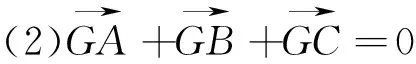
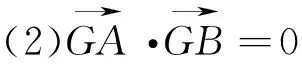
不難看出，對同一“提示語”的不同理解產生的思維起點不盡相同，不同的“提示語”下的思維起點卻有可能相同，比如“重心”和“垂直”均可以從解析幾何、向量等角度展開思維，同時也表明了不同的思維起點將會在過程中與其它信息產生交匯聯系，形成一個和諧統一的邏輯結構.在教學中，讓不同的學生暴露其表征已有信息的過程，并進一步暴露其產生的思維起點，讓其他學生從中獲取經驗，長期訓練，學生的表征能力將會得到很大提升.

2.模式構建，體現思維范式的引導性

我們經常遇到這樣的現象：

課堂直接給出某一公式(定理)，然后給出大量訓練題直接“運用”這一公式(定理)；

將某一問題改換敘述方式，或呈現新的情境，很多學生就束手無策.

上述現象是就題做題的短視教學行為，內在原因是教師沒有將知識的生成、推導過程暴露給學生，必然不能揭示出過程中所蘊含的數學思想方法，學生在知識運用時出現思維卡殼斷層的現象就不足為奇了.人教社章建躍教授在《中學數學課改的十個論題》中就著重指出：“要強調知識及其蘊含的思想方法教學的重要性.”因此，我們在新知識的教學中(特別是一些核心知識)，必須要不遺余力、不惜時間地體現出其過程性，并提升至思想觀念層面去指導知識運用.

本題的思想方法源自哪里？我們回顧一下課本中推導“正弦定理”的過程：

傳統推導正弦定理的基本方法有三個：

(暴露過程)

方向1：作高法——從幾何量關系的角度去研究，蘊含“算兩次”的基本思想；

方向2：坐標法——從解析幾何的角度去處理，體現代數方法研究幾何問題的基本準則；

方向3：數乘法——從向量運算的角度去思考，突出向量關系數量化的基本要領.

(小結提升)獲得的思想方法：解決三角形(或幾何圖形)有關問題可以從幾何關系、解析幾何、向量運算三個基本方向進行思考.

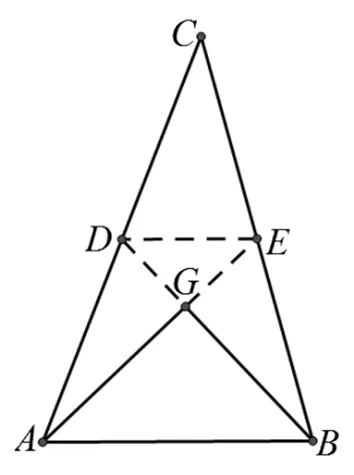
圖2

通過暴露過程，小結提煉等活動的設計，為學生提供了具有思想性的先行組織者，在遇到類似問題時，就會自覺地將此作為一種思維的范式去進行：

本題是研究三角形中有關量的問題(問題識別)，可以將此與“正弦定理”的研究過程產生聯系，從幾何量的關系、解析幾何、向量運算三個視角去展開思維(模式操作).

方向1：幾何量的關系入手

分別延長AG、BG交BC、AC于E、D(如圖2)，由勾股定理得

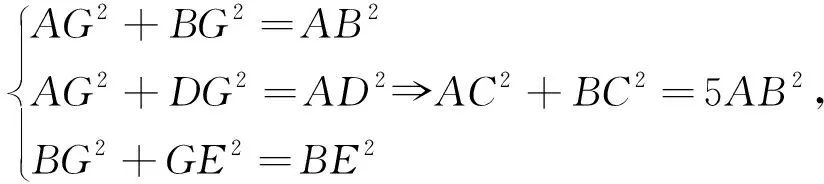
到體現.

方向2：解析幾何的方法研究

圖3

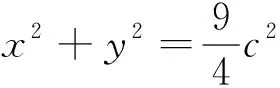
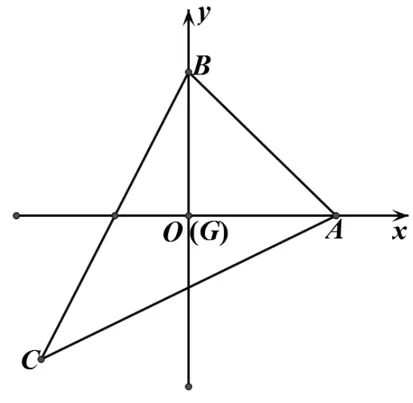
圖4

建系2：注意到垂直的特殊性，以G為坐標原點，分別以AG、BG所在直線為x,y軸建立坐標系(如圖4)，設A(a,0),B(0,b),C(-a,-b)，接下去可通過等面積、向量運算等進行處理.

方向3：向量運算著手

從上面的具體解答可得到驗證，一旦有了核心知識蘊含的思想方法作為范式，學生必定能迅速進入思維通道.因此，在知識教學中一定要重視挖掘和揭示知識的思想性，并在知識運用過程中加以示范與訓練，定會提升學生數學認知的理解程度.