數形結合在高考解題中的應用

安徽淮北師范大學數學科學學院 (235000)

方 成 張 昆

數學是研究數量關系和空間形式的一門科學，簡單的來說，就是研究“數”和“形”兩大部分．數量關系中蘊藏著幾何模型，幾何中又涉及到數量關系．[1]其中，圖形具備形象直觀的優點，通常用于定性分析；而數量關系則需要依據數據進行分析．因此，在數學解題活動時，若能找到途徑，將“數”和“形”兩者形成有機結合，必能取長補短，會對探究問題的思路起到顯著效果．對此，著名的數學家華羅庚先生曾說：“數與形，本是相倚依，焉能兩邊飛？數缺形時少直觀，形少數時難入微，數形結合百般好，隔家分家萬事休，切莫忘：幾何代數統一體，永遠聯系，切莫分離．”[2]數形結合的思想已滲透到中學數學學習中，因此，在高考解題活動中，考生對某些特定問題的具體特點，選擇以形助數或以數解形的途徑是一條發現解決問題思路的比較好的手段．

一、求方程根的個數方面的應用

求解一般形式的方程的根的解法多樣，例如配方法，求根公式等等．對于一些特殊形式的方程，考生們通常手足無措．這時候，可以轉換另一種解題思路，將方程的根轉化為函數的零點問題．而函數的零點是函數圖像與x軸交點的橫坐標，這涉及到圖形方面的知識，而方程的根屬于代數方面的內容．由此將代數與幾何聯系在一起．數形結合思想是將其聯系在一起的一條支鏈．當選擇一般途徑解決不了代數問題時，可以借助“數形結合”轉化思想，從“圖形”方面考慮問題，進而尋求解決問題的途徑．

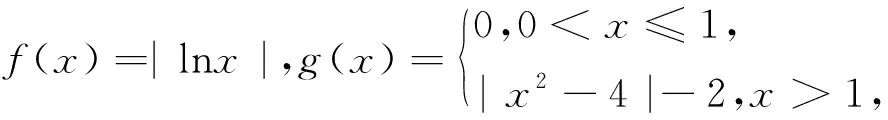
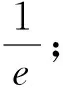
圖1

解法2：由|f(x)+g(x)|=1，可得g(x)=-f(x)±1，分別作出函數的圖像，分情況討論：g(x)與h(x)=-f(x)+1的圖像如圖1所示，圖像有兩個交點；g(x)與φ(x)=-f(x)-1的圖像如圖2所示，圖像有兩個交點.所以滿足方程

|f(x)+g(x)|=1的實根的個數為4．故答案為4．

圖2

點評：比較這兩種解法，可以看出運用方法二，從圖像上直觀看出有四個交點，方法簡便．將方程的根與函數圖形的交點聯系一起，直觀看出根的個數．而方法一分類過程較為復雜，且容易出錯，學生在解題中遇到求函數單調性來判斷函數是否與x軸存在交點問題，這一類問題容易造成學生思維障礙，求解過程受阻，不易解決．因此，繞過原來的思維障礙，直接從圖形角度出發來解題．

二、求參數取值范圍中的應用

參數，一般稱為參變量或參變數，指相對于未知數來說可以在一定范圍內取值的常數值或聯系不同未知數之間的相關的未知數．求參數取值范圍是高中數學中常見的一類問題，也是高考考查的重點之一．波利亞的思維方法表明：時刻不忘未知量．[3]所以在求參數取值范圍的求解問題時，涉及的未知量很多，解題方式靈活多變．因此試著利用數形結合思想巧解這一類型的題目．

例2 (2014山東理8)已知函數f(x)=|x-2|+1,g(x)=kx．若方程f(x)=g(x)有兩個不相等的實根，則實數k的取值范圍是( )．

解析：由題意知，首先畫出函數f(x)=|x-2|

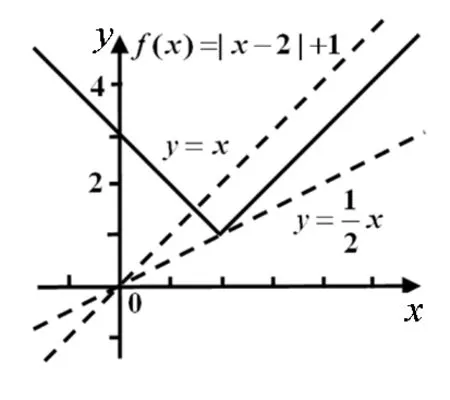
圖3

點評：求參數的取值范圍的一般解法是分離參數，再求參數的取值范圍．在此期間，不免加入了較為復雜的運算，所以求參數的取值范圍的另一有效手段是借助圖形，通過函數圖像萌生出新的解法，而這種巧妙的解法比一般方法更加簡潔．所以它在一定程度上有助于激發學生的創造性思維，并且起到事半功倍的效果．

三、求線性規劃中的最值問題

線性規劃問題是高考常見的考點之一．其中一類問題是求線性目標函數在線性約束條件下的最值問題，并把滿足這個條件的解的集合稱為可行域．線性規劃中求最值問題借助圖形能夠直觀的反映出來，“以形助數”，幫助考生解題．

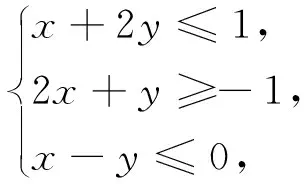
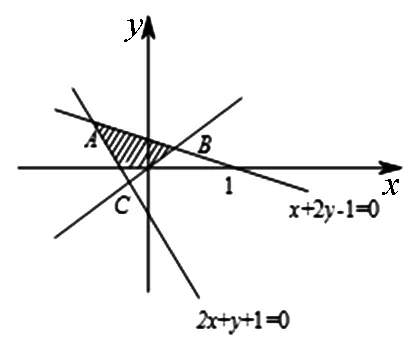
圖4

分析：不等式組

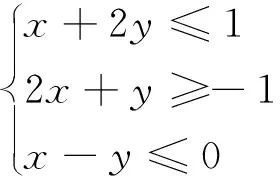
點評：本題的關鍵在于根據約束條件，準確做出可行域，利用數形結合找出最優解．

四、三角函數中的應用

研究三角函數的某些性質，往往借助圖像法才能更好的解決對應的三角函數問題，借助圖形轉變能夠直觀的反映三角函數圖形的性質，例如對稱軸，平移后的函數圖像，平移后的函數解析式等．

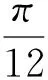
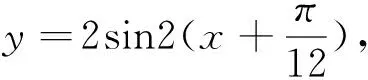
點評：數與形是數學的兩大支柱，數形結合思想關鍵在于如何將數與形結合起來，通過圖形研究三角函數的性質，直觀分析，從而為發現解題思路創造條件．

五、幾何概型中的應用

幾何概型是指每個事件發生的概率只與構成該事件區域的長度(面積或體積)成比例，它屬于概率論與統計學范疇．但其中也蘊含著數形結合的思想，下面以16年新課標高考數學的一道客觀題為例．

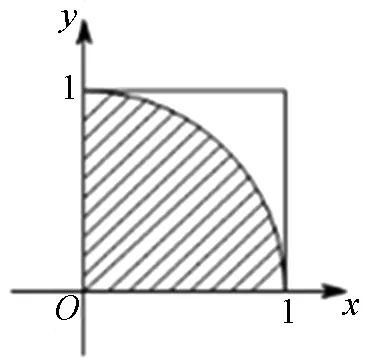
圖5

例5 (2016新課標理數2卷)從區間[0,1]隨機抽取2n個數x1,x2,…,xn,y1,y2,…,yn構成n個數對(x1,y1),(x2,y2),…,(xn,yn)，其中兩數的平方和小于1的數對共有m個，則用隨機模擬的方法得到的圓周率π的近似值為( ).

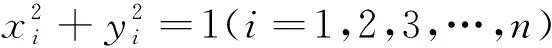
點評：幾何概型求概率是與構成該事件區域的長度(面積或體積)成比例，而面積和體積往往要借助圖形，通過對圖形進行觀察，再利用代數方法求出概率．故數形結合思想應用其中．

六、解析幾何中的應用

解析幾何，將數與形緊密的結合在一起，笛卡爾曾經寫道：古代人的幾何和現代人的代數，都是研究非常抽象、毫無用處的題材，前者局限于考察圖形，后者一味用規則和數字來約束，因此要找出另一種方法，包含它們的長處，沒有短處．[4]故解析幾何就很好的通過數量分析研究幾何圖形及其變化,是數與形的緊密結合．

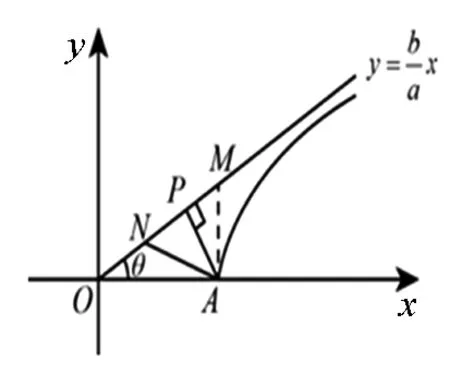
圖6

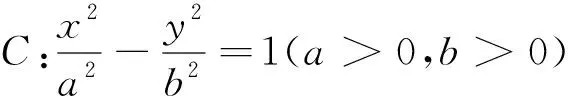
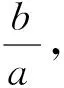
點評：該題巧妙的利用了數形結合的思想，以數解形，借助幾何軌跡所遵循的數量關系，與幾何定理相結合．找尋雙曲線中各個系數之間的數量關系，再結合勾股定理，三角函數等求出雙曲線的離心率．以形助數，以數解形，巧妙解題．

七、結語

問題解決，其實就是找到問題題設條件與所求結論之間的聯結，而題設條件與所求結論之間存在著某種千絲萬縷的聯系．如何解題，就是要找出其中蘊含的某種關系．[3]數學的解題過程就像是抽絲剝繭一樣，層層分析，步步為營，在變中找尋不變．而一旦解題過程中受阻，就要嘗試轉化思路，從另一個角度去分析問題，從而到達終點．在索解思路時，如果一味使用代數法或者幾何法，很可能找不到解決問題的思路，或者陷入繁雜的計算中去．數形結合是比較好探索思路的方法．比如在求方程的根，函數的零點，不等式等等，如果用一般的方法不能解決時，就要轉化思路，將它與圖形聯系起來，以形助數．同樣的，如果解決某一圖形時，試著找出圖形之間的數量關系，用代數方法解決幾何問題，又或是數形兼顧．因此數形結合在高考數學解題中具有獨特的策略指導和調節作用．