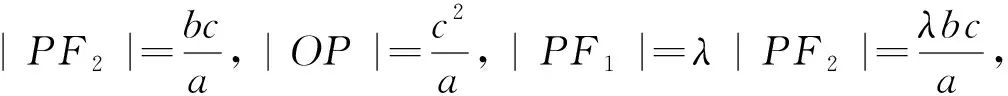2018年高考數學全國卷Ⅲ理科11題研究

四川省安岳教師進修學校 (642350)

羅 家

云南省昆明市西山區粵秀中學 (650011)

舒前銀

2018年高考數學全國卷Ⅲ理科第11題：

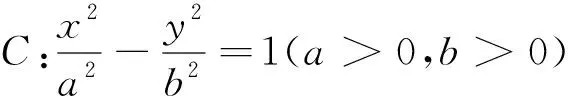
這道試題以直觀想象、邏輯推理和數學運算等核心素養立意，其思路寬、解法多、可推廣，富含思維價值，值得研究.

一、試題解法探究

G.Bolya在《數學的發現》序言中說“數學的首要任務就是加強解題訓練”，同時G.Bolya還曾說過“掌握數學就意味著善于解一些要求獨立思考，思路合理，見解獨到和有發明創造的題.”由此可見，解題研究在數學活動中占十分重要地位.而解法研究是解題研究的主要內容.對高考試題的解法研究可以從一題多解入手.

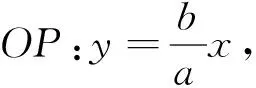
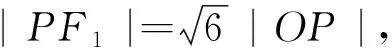
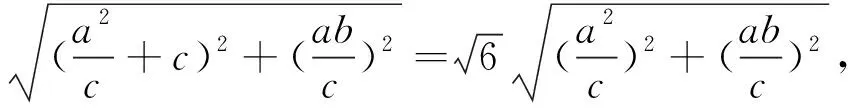
評析:本法主要利用雙曲線的漸近線、直線的位置關系、點與點距離公式、雙曲線a,b,c的幾何性質進行解答，解題思路顯而易見，但計算量相對比較大.

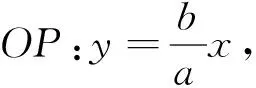
|PA|×c=ab.

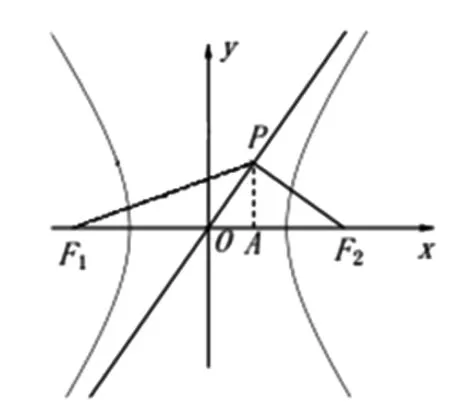
圖1

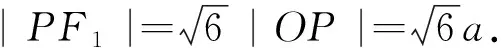
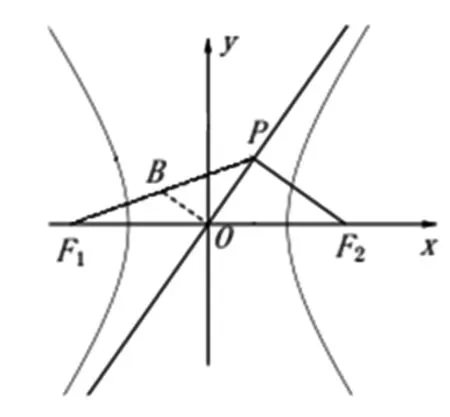
圖2

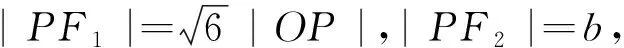
圖3

解法四：由解法二可知,|PF2|=b,|OP|=a,過F1作F2P的垂線，交F2P的延長線于D，則OP為中位線.

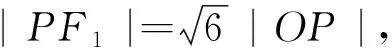
評析:上述三種解法重點利用雙曲線的漸近線、幾何性質、數形結合思想等，在考查離心率問題時，如果沒有給出a,b,c具體的值時，在解答過程中可將a,b,c中任意一個設為具體的特殊值，可以大大簡化計算.

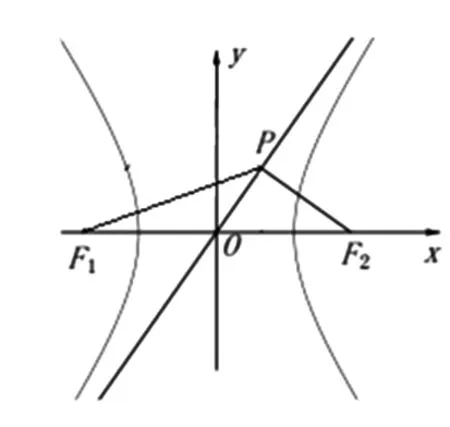
圖4

解法五：由解法二可知，|PF2|=b,|OP|=a,

在Rt△OPF2中，因為

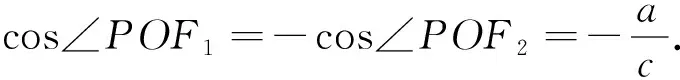
評析:此法仍利用雙曲線的漸近線、幾何性質，表示出△F2PF1三邊及|F1F2|邊上中線的長，不難聯想到解三角形問題，利用直角三角形中三角函數的定義、誘導公式及余弦定理，建立a,c的方程，進而得到離心率.

圖5

解法六：引理(中線定理又稱阿波羅尼奧斯定理)：在ABC中，設M是BC的中點，AM為中線，則|AB|2+|AC|2=2(|AM|2+|MC|2).

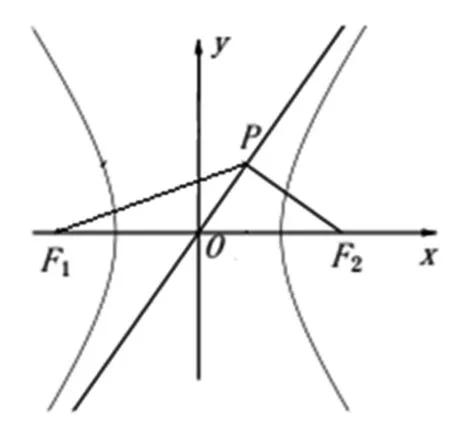
圖6

評析:此法仍利用雙曲線的漸近線、幾何性質，表示出△F2PF1三邊及|F1F2|邊上中線的長，進而想到了中線定理(pappus定理),直接利用定理大大簡化了計算.

二、試題的推廣

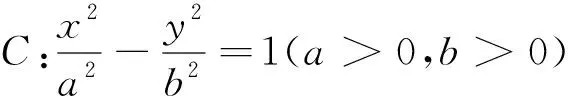
證明:由解法二可知|PF2|=b,|OP|=a,

|PF1|=λ|OP|=λa,由中線定理可得|PF1|2+

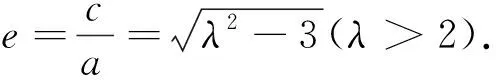
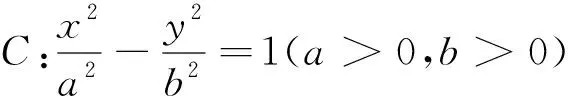
證明:由解法二可知|PF2|=b,|OP|=a,

|PF1|=λ|PF2|=λb.

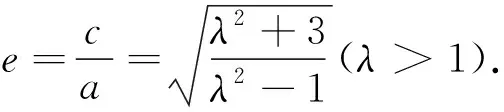
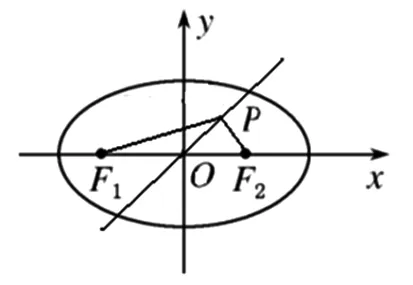
圖7

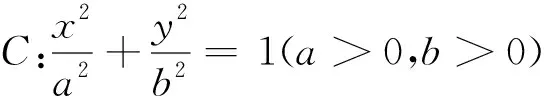
證明:由點到直線的距離公式可得|PF2|=

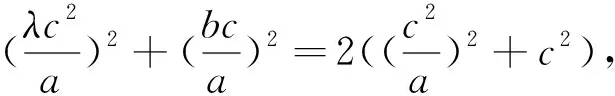
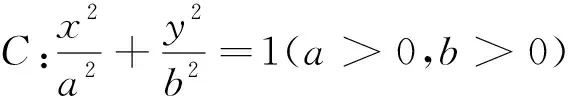
圖8