構建數學模型提高中學生創新意識

安徽省六安市皋城中學 (237000)

李 剛

創新是引領發展的第一動力.抓創新就是抓發展，謀創新就是謀未來.黨的十八大以來，以習近平同志為核心的黨中央把創新擺在國家發展全局的核心位置，圍繞實施創新驅動發展戰略，加快推進以科技創新為核心的全面創新.在基礎教育階段，中學數學應該承擔起培養學生創新意識的責任，為社會所需要的創新型人才提供支持.

《義務教育數學課程標準》(2011)第二部分課程目標提出：通過義務教育階段的數學學習，學生能“了解數學價值，提高學習數學的興趣，增強學好數學的信心，養成良好的學習習慣，具有初步的創新意識和科學態度”.

數學是研究事物之間和事物內部空間形式與數量變化規律的科學，在中學數學教學中，數學模型思想的滲透，數學方法的掌握，數學思維的形成，在實際中往往只有通過大量做題來實現.要改變這樣的現狀，最有效的途徑就是通過適當的方法，培養學生的創新思維.下面就如何在中學數學的課堂中通過數學模型的方法提高中學生的創新思維進行一些簡單的探討.

一、從普通問題入手，培養創新思維

生活中，很多會品茶的人品茶的時候都講究一個氛圍，一杯清茶，圍著不疾不徐的風雅琴韻，這就是氛圍.在中學數學教學中創設適當的情景氛圍，比如，利用現代化的多媒體設備，他能巧妙地融音樂、圖片、動作表情于一體，教師可以充分運用錄像、投影、幻燈片，音響等設置情境氛圍進行教學，能最大程度的激發學生學習的興趣，使他們樂于投入到數學學習中來！

比如，抓住中學生對做游戲比較感興趣的貪玩心理，在講解“相反數”一節時，如何生動形象的讓學生理解相反數的概念，可以在課堂上做個小游戲，讓一名同學站在講臺上，面向大家，然后喊口令“向后轉”，分別轉一次，轉兩次，問這位同學每次所面對的方向如何？學生自然很容易就能明白1,-1,-(-1)這一類概念的區別與聯系.

再如，在找規律中，有這樣一組數：

1+3=4=22

1+3+5=9=32

1+3+5+7=16=42

……

從中不難得出前n個奇數的和為n2這個結論，對于很多學生來說這是一個懸念，它可以從幾何圖形上面得到進一步的直觀的解釋.

圖1

一個方塊的面積為1，增加3個方塊，則變為一個2×2的方塊，它的面積為4；再增加5個方塊，則變成一個3×3的方塊，它的面積為9，依此類推.如圖1.

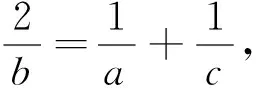
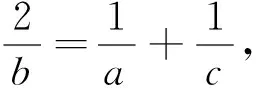
該例說明，我們在訓練學生的解題思路和方法時,要有選擇,有控制地給學生提一些典型的、特殊的思想和方法,循序漸進地開拓學生的解題視野,使他們在思想方法上,在尋求解決問題的途徑中能夠做到前后知識互補、互相促進,克服學習中的畏難情緒,培養自強不息和積極向上的學習精神,讓學生視野遠大,心胸開闊,思維活躍,學習主動,才能逐步達到學習目的.

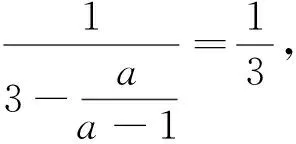
分析：求解的常規思路把a用任一數替換，驗算等式是否成立.

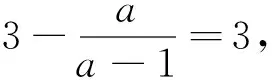
培養中學生數學創新思維能力的方法很多，但必須做到科學、適度，而且要有難度，必須在學生的“最近發展區”內.采用數學模型的思想方法，對教師的教學設計水平和學生的學習指導有幫助，對學生的影響很大.影響可以分為兩個方面：一方面，影響學生的學習過程，改變傳統的學習方式，可以引起學生的學習興趣，激發學生對數學問題的應用探索和求知欲，在數學建模中建立創新意識和創新能力.另一方面培養和提高學生的合作精神和團隊意識，培養學生自律的良好品質，這些對于后續課程的學習和獨立研究，都有很大的好處，最后提高學生的可持續發展，培養學生適應現代社會要求的素養.

二、構建數學模型，提高創新意識

《義務教育數學課程標準》(2011)指出：模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑.建立和求解模型的過程包括，從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數學關系和變化規律，求出結果并討論結果的意義.這些內容的學習有助于學生初步形成模型思想，提高學習數學的興趣和應用意識.

數學模型是人們為了得到一個特殊的研究目標，按照目標的獨特內涵，建立一種具有抽象性、簡化性和趣味性的數學結構，即現實生活中的數學問題在研究的過程中用數學的方式構造出來.數學建模是假設簡化現實生活中問題的背景和所依據的數學模型的目的，找出未知數和相關參數之間的關系，并用字母表示未知數求解;采用相應的物理或其他規則，使用數學問題變量建立數學公式和參數列表即確立數學模型計算的解決方案，解答數學問題.用這個答案解釋生活中的原數學問題，最后把上述結果用實際情況來驗證，并用來處理多周期的實際問題和研究問題的深化過程.

利用數學建模，一方面可以引導學生積極的去探索數學問題和激發他們的求知欲，提高他們學習數學的興趣；另一方面培養和提高學生的合作精神和團隊意識，培養學生良好的品質，如嚴謹和自律等，這為后續課程的學習和自主學習，都有很大的好處.

數學模型的建立過程就是數學模型的本質，即數學知識應用到實際問題轉化成概括性的邏輯思維的數學關系的變化，然后處理所有相應的數學模型，形成之間的數學關系.數學建模過程可以表示在以下五個方面：

分析問題過程：了解問題的實際背景材料的性質，分析和找出問題的目的.

問題的假設化簡：把影響研究目標的必要成分找出來，把次要成分忽略掉，這樣雜亂無章的數學問題就被概括成具體問題.

↓

數學模型的建立：數學模型是要建立在原先假設的基礎上，通過運用適當的數學工具和數學知識來刻畫變量之間的數量關系，因此得到相應的數量結構.

求解數學模型：根據數學模型分析，用數學方法和計算機程序來求解數學建模.

模型的驗證分析：檢驗模型是不是與實際相符合，并對它做出詮釋.

(一)函數模型

在解決實際問題時，存在函數關系的數學問題時可以建立函數模型.

例3 某家服裝店進了一批衣服，一件衣服的進價為48元，為了獲得更多的利潤，售價要高于進價，經過觀察可得，當每一件的價格是60元時，每月有180件衣服售出，當每一件衣服價格是75元時，每月有105件衣服售出.如果商店衣服不積壓，忽略其他因素，則在售價為多少時，所獲利潤最大？最大是多少.

分析:題設中并沒有指出售價與銷售量之間的函數關系，只是告訴大家在兩種不同價格下的銷售量.所以，教師可以通過帶領學生觀察實際生活中的真實銷售問題，分析得到：售價越高，銷售量越低的規律，構建簡單一次函數的數學模型，假設售價x與銷售量y之間的函數關系為y=kx+b的一次函數形式.

解：由題意得，設這個函數的解析式是y=kx+b,則有

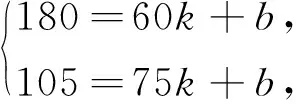
函數模型常用來解決利潤，增長率，路程，面積的大小等問題.這些問題可以通過日常的真實體會，得到一般性的規律，然后根據這一規律，構建適當的數學模型進行求解.當然，上述問題，除了引導學生思考簡單的一次函數模型之外，還可以啟發學生，是否還有其他的模型(不是一次函數模型)可以刻畫“售價越高，銷售量越低”的規律呢？在相應的模型下，價格和最大利潤分別又是多少呢？相信在學生中會有很多具有新意的討論.除此之外，還可以進一步啟發學生：實際情況中，積壓是很常見的現象，如果出現了積壓，那么售價又該如何決策，才能達到利潤最大呢？

(二)不等式(組)模型

我們要解決存在不等關系的實際問題就得使用不等式的思想去解決，所以我們要建立不等式(組)模型.

例4 某校組織學生參加郊游，需要在某賓館住宿一晚，假如每個房間住4人，那么就有20人住不下；一樣的房間，假如一間房住8人，那么還有一間不滿也不空.請問：這所學校有多少學生參加春游？

分析：啟發學生，真實的情況中，房間的個數必須是整數.

解：設他們需要x間房，由題意得

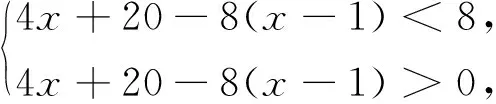
解得5

不等式(組)模型可以用于產量的估算，決定是否投資，虧盈的分析，價格的核對等，在實際經濟生活中廣泛應用.

(三)方程(組)模型

在我們解決實際問題中，遇到用方程性質解決的問題時，可根據實際問題的已知條件，設出合適的未知數，找出相等的關系，最后檢驗算出的結果是否符合題意.

例5 2019年的新年快到了，某玩具廠要生產一批有豬形狀的新年吉祥物甲，乙兩種，該玩具廠主要用A，B兩種原料.已知需要用A種原料和B種原料分別為4盒和3盒才能生產一套甲吉祥物，需要用A種原料和B種原料分別為5盒和10盒才能生產一套乙吉祥物，玩具廠購進20000盒A原料和30000盒B原料.如果原料沒有剩余，求這個玩具廠生產兩種吉祥物各多少套？

分析：在解決實際問題中應用廣泛，例如人員調配，工程實施，產品購銷等，都可以建立方程(組)模型解決.

解：設生產甲種吉祥物x套，乙種吉祥物y套，由題意得

從而，如果原料沒有剩余，則這個玩具廠生甲乙兩種吉祥物分別為2000套和2400套.

教師在帶領學生分析問題的同時，也要啟發學生，現實生產中，原料有沒有剩余或者短缺？如果剩余了或者短缺了，我們又應該如何處理問題？諸如此類的問題，可以一步一步帶領學生構建更加貼近生活的數學模型，激發學生學習的興趣.在整個過程中，我們也會發現學生會提出一些非常具有創意的想法.如果能夠合理加以引導，學生的思路遠比我們想象的還要具有創意.

總之，數學模型在解決實際問題中的使用，不僅能夠理論聯系實際，而且學生的學習興趣在解決問題的過程中也隨之提高，從而提高學生掌握數學知識的能力和理解，還會更好的把數學思想方法用到解題過程中去，加固學生的數學知識結構.解題的過程中，學生敢于質疑，開闊自己的求異思維，獨自去思考和探索，去提出自己的新觀點，新思路，新方法.同時可以加深對探索和創新思維的培養，發展學生自主探究能力，從而提高學生的創新能力.