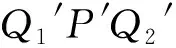一道高考理科數學題推廣的進一步研究

陜西安康學院數學與統計學院 (725000)

趙臨龍

2012年安徽省高考理科數學20題如下：

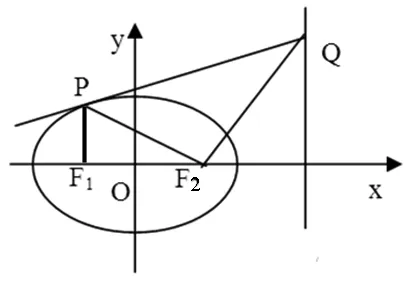
圖1

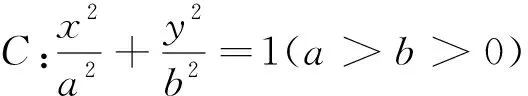
(Ⅰ)如果點Q的坐標是(4,4)，求此時橢圓C的方程；

(Ⅱ)證明：直線PQ與橢圓C只有一個交點.

文[1-2]將橢圓的切線擴展為2條，給出新結論,文[3]將橢圓的焦點擴展為2個，又給出新結論.文[4]將橢圓推廣到雙曲線，給出相關結論.但在這些結論中，有些是本題的內在特性，而有些并非是本題的內在特性，甚至有些結論是錯誤的.

文[5]對出現的問題進行討論，但遺憾是文[5]可能是由于版面緊張，只有討論過程而沒有結論.現結合相關問題，將橢圓推廣到中心二次曲線，給出相關結論，以完善相關結論.值得注意是，要揭示本題的內在屬性，需要借助射影幾何的知識.

1 知識準備

定義[6]如圖2.過點P(x0，y0)引二次曲線Γ：

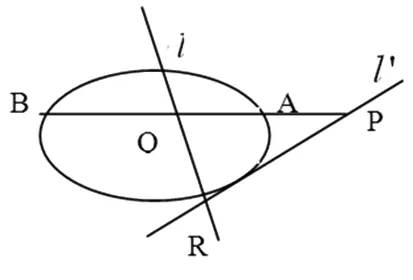
圖2

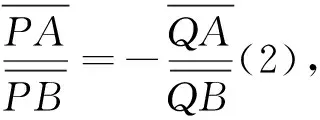
引理1[5]若點P關于二次曲線Γ的極線為l，則l上一點Q關于二次曲線Γ的極線l'必過點P.

引理2[5]兩極點P、Q對應極線分別是l和l'，則l和l'的交點R關于二次曲線Γ的極線為直線PQ.

推論1 中心曲線Γ的焦點關于Γ的極線是其對應準線.

2 命題討論

圖3

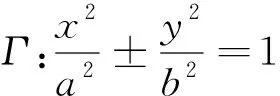
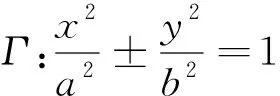
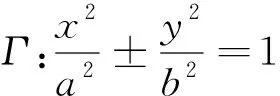
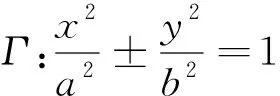
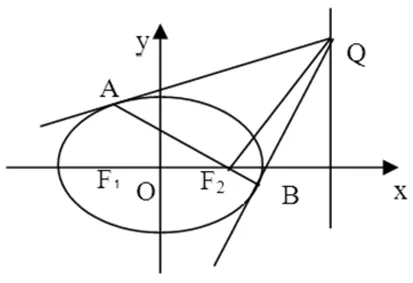
圖4

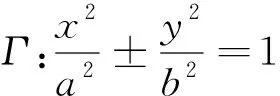
證明：如圖，兩切點A、B的極線AQ、BQ相交于極點Q，則極點Q的極線為AB.由于極點Q在焦點F2一側的準線上，則極線AB必過焦點F2.由定理1，得到QF2⊥AB.

推論2 過中心曲線Γ相應于焦點F2一側的準線上任意一點Q與Γ的焦點F2的連線垂直于點Q關于Γ的極線.

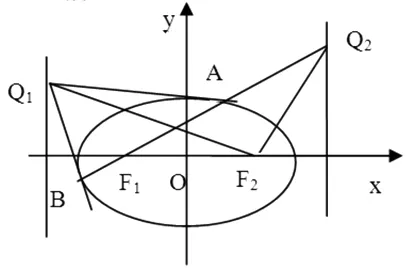
圖5

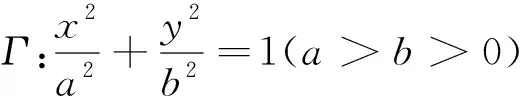
證明：如圖，由于極點Q1的極線為AB，極點F2的極線為其準線，且兩極線交于點Q2，則極點Q2的極線為Q1F，于是由推論，得到：Q2F2⊥Q1F2.同理，Q1F1⊥Q2F1，則有結論.

推論3 過中心曲線Γ相應于焦點F1、F2的準線上的點Q1、Q2關于Γ的極線分別為Q2F1、Q1F2，則四點Q1、Q2，F1、F2在以Q1Q2為直徑的圓上.

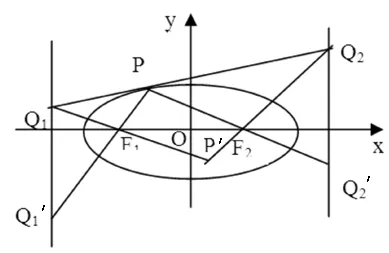
圖6

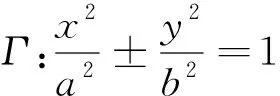
證明：如圖，點Q1、Q2關于中心曲線Γ的兩極線PF1、PF2交于Γ于點P，于是以兩極線PF1、PF2交點P為極點關于中心曲線Γ的極線必過點Q1、Q2，即Q1、P、Q2三點共線.由定理2，知直線Q1PQ2切中心曲線Γ于點P.現設當點P是中心曲線Γ的切線Q1PQ2時，則Q1′是極點F1、Q1分別對應準線Q1Q1′、