考慮P2G的多能源系統優化運行研究*

唐春童，李曉露，單福州，宋燕敏，周海明，劉超群

(1. 上海電力學院 電氣工程學院，上海 200090； 2. 中國電力科學研究院有限公司，北京 100080)

0 引 言

隨著化石燃料的日益枯竭和環境污染問題嚴峻，開發清潔的可再生能源和提高能源的利用效率變得越來越重要。而就目前而言，新能源的使用中，棄風、棄光現象比較嚴重，究其原因，是目前能源系統規劃單一，僅從單獨的特定能源規劃，這就造成了可再生能源極大的浪費，能源的利用效率低下[1]。為此，打破原有各能源供能系統單獨規劃、設計和運行的傳統模式，綜合協調包括電能、熱能和天然氣等在內的多種能源的聯合運行，反映多能源系統運行的特性，并最終實現一體化的綜合能源系統，是實現社會用能效率最優、提高可再生能源使用效率、實現能源可持續發展的必經之路[2]。為實現多種能源相互之間的互聯和共享，文獻[3-4]引入了能源互聯的概念，對電力系統、交通系統、天然氣系統等多個能源系統相互之間的融合給出了整體性的理論分析和架構搭建。文獻[5]介紹了實現能源互聯的關鍵組件，其包括電力-天然氣耦合組件、電-熱耦合組件等，并且還引入了在多能源系統規劃、運行研究中重要的一個概念，即能源中心[6]。文獻[7]分析了多種能源轉化過程中能量之間的等效關系，并以此構建了能源之間的等效替代模型，但該文僅僅關注了電能與冷熱能之間的轉化，未涉及電與氣之間的轉化關系。針對此問題，文獻[8-11]對涉及電能-天然氣轉化的方面進行了研究。文獻[8-9]中電能與天然氣僅通過燃氣機組相互聯系，只是天然氣單向地轉變為電能，忽略了電能和天然氣之間的互補替代。文獻[10-11]則是從目前日益成熟的電轉氣技術(P2G技術)入手，結合CHP機組等相關設備，實現了電能和天然氣之間的相互轉化，再結合能源中心的概念實現對多能源系統的規劃和分析。它們都是以系統運行成本最優為目標函數，但其中沒有考慮P2G設備的運行成本。而文獻[12]指出，當前P2G設備運行成本高昂，單獨地參與電力-天然氣系統優化運行所獲得收益無法滿足系統運行成本的支出。文獻[13]經過算例仿真，也得出了僅通過P2G廠站實現電力系統與天然氣系統的耦合，在成本和可靠性方面無法取得收益。

當前，P2G設備主要用于消納風能等可再生能源發電產生的過度電量，從而減少“棄風”、“棄光”等現象。針對“棄風”問題，文獻[14]為棄風成本函數設置了一個固定的懲罰因子，棄風成本就等于懲罰因子與棄風量的乘積。相較于固定的懲罰因子，分段懲罰因子可以根據風電場棄風量的多少設置不同的懲罰因子，更能體現對風電場“棄風”行為的制約作用。

研究了在多能源系統中，考慮P2G設備運行成本的情況下，系統供能成本變化以及風電消耗問題。首先，基于能源中心的建模方法對包含P2G設備在內的多能源系統進行建模。之后，建立包含考慮分段棄風懲罰因子的棄風成本在內的多能源系統運行優化模型，并采用粒子群算法進行求解。最后，根據算例驗證分析了P2G設備對降低系統整體供能成本和消納風電方面的效益。

1 含P2G設備的能源中心模型

傳統電力系統和天然氣系統之間的耦合僅限于燃氣輪機，即天然氣向電能單向轉換。近年來出現的電轉氣(P2G)設備則改變了這一現狀[15]。P2G設備是一項將電能轉化為燃料氣體的設備。目前，P2G設備主要是應用于在可再生能源過剩的情況下將多余的電能轉化為天然氣，通過實現電能和向天然氣的轉化，能夠將傳統的天然氣網絡和電網絡更深層次的結合起來，這使得它在多能源系統運行中有著更深層次的應用。

采用的能源中心模型，包含了多種能源轉換設備，其中包括P2G設備，它能夠實現電能向天然氣的轉換；燃氣輪機，它能夠將天然氣轉換成電能和熱能；燃氣鍋爐，它能夠實現天然氣向熱能的轉換。其示意圖如圖1所示。

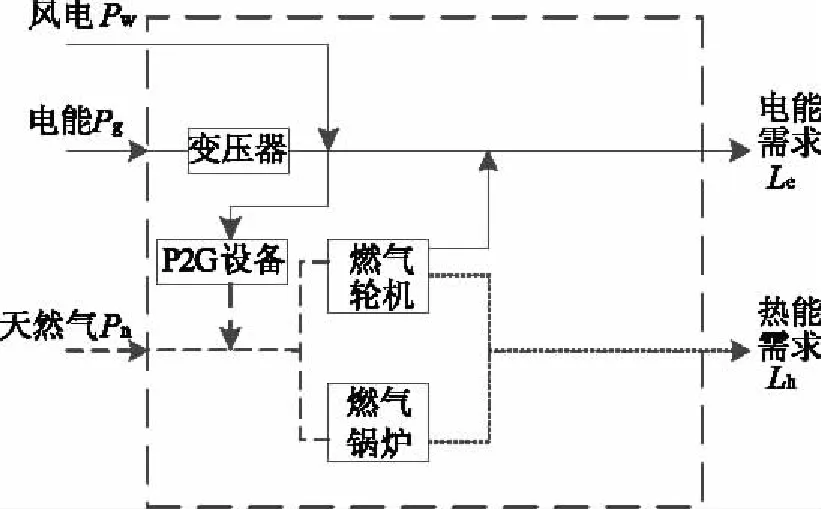
圖1 能源中心示意圖

能源中心中，多種不同形式的能源可以進行轉換、調配和儲存，它代表了不同能源設施或負荷之間的接口。能源中心在輸入端消耗功率，通常與電力和天然氣能源設備聯系在一起，而在能源中心的輸出端，通常會輸出用戶所需的各種能源形式，如電能、熱能、冷能等。能源中心里的轉換設備在輸入和輸出端口之間建立了冗余連接。在多能源系統中，能源中心所帶來這種冗余能夠帶來兩個重要的好處：(1)對負荷側而言，供能的可靠性得到了提升，因為在能源中心里不再是單一的網絡供能；(2)額外的自由度能夠實現能源中心供能的最優化。

能源中心中輸入載體和輸出載體之間的映射可以通過一個耦合矩陣M來進行數學建模。假設能源中心中涉及到的能源載體分別記作α，β，…，ω，可以對應包含天然氣、熱能、電能、生物質能等一系列能源在內的多種能源形式。其中，每個能源載體都可能出現在輸入端或輸出端。輸入能源和輸出能源端各載體的輸出功率可以定義為Iα，Iβ，…，Iω以及Oα，Oβ，…，Oω。則能源在輸出端口和輸入端口之間進行轉換的方程式可以描述為：

(1)

式中M矩陣是能源轉換的耦合矩陣，它表示的是能源轉換設備的轉換效率和能源中心的拓撲結構。對單獨的能源轉換設備而言，經由耦合矩陣Mαβ將α形式的能源轉換成β形式的能源的過程可以描述為：

Oβ=MαβIα

(2)

對單輸入-單輸出的能源轉換設備，耦合系數就等于其轉換效率，只要設備的轉換效率是固定的，耦合矩陣就表示為輸出能源和輸入能源之間的線性變化。

2 計及棄風成本的多能源系統優化運行模型

2.1 目標函數

采用的多能源系統優化運行模型以調度時間內，計及棄風成本時，系統的供能成本最小為優化目標，具體如式(3)所示：

minFtotal=Ff+Fo+Fd

(3)

(4)

(5)

(6)

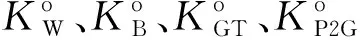
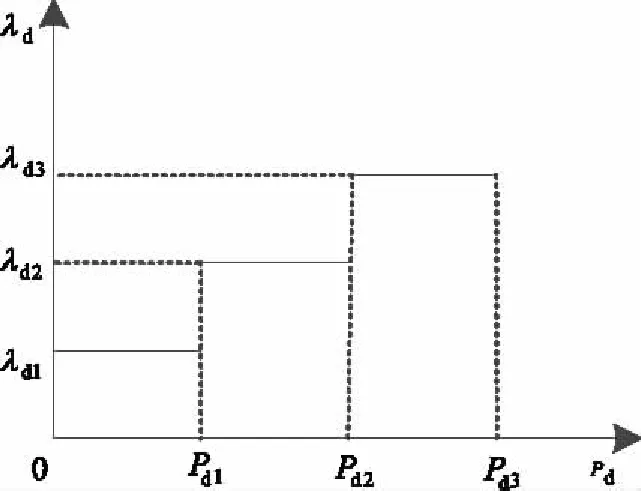
圖2 風電棄風功率分段懲罰因子

采用分段遞增懲罰因子后，某段時間內棄風功率越大，該段的懲罰成本也就越大，如圖3所示。

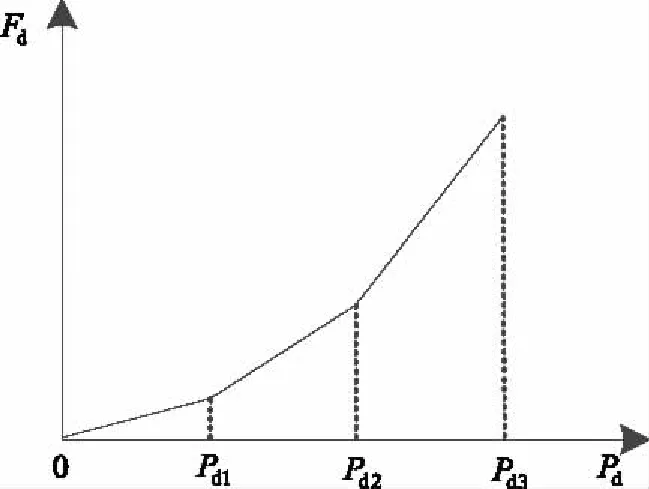
圖3 風電棄風功率分段懲罰函數

2.2 內部約束

內部約束條件主要包括以下幾個約束，具體為：

(1)燃氣輪機運行約束

0≤Pgt(t)≤Pgt.max(t)

(7)

0≤Pct(t)≤Pct.max(t)

(8)

式中Pgt.max(t)為燃氣輪機電能輸出上限；Pct.max(t)分別為燃氣輪機熱能輸出上限。

(2)燃氣鍋爐運行約束

0≤PB(t)≤PB.max(t)

(9)

式中PB.max(t)為燃氣鍋爐熱能輸出上限。

(3)P2G裝置運行約束。

0≤PP2G(t)≤PP2G.max(t)

(10)

式中PP2G.max(t)為P2G裝置轉化的電功率上限。

2.3 外部約束

(1)系統功率約束

針對上節分析的能源中心耦合模型，本文中輸入能源包括火電、風電和天然氣，輸出能源，即系統負荷需求主要為電能需求和熱能需求，根據能源中心中多種能源轉換設備的不同轉換特性，由上式(1)給出了系統的耦合方程，也就是系統運行的等式約束。

(11)

(12)

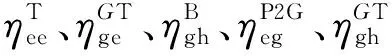
(2)風電機組運行約束

(13)

式中Pe為風機的額定輸出功率；νi表示風機切入風速；νo表示風機切出風速；νe表示額定風速。

2.4 模型求解

所建立的優化模型為非線性優化問題，目標函數較為復雜，含有大量約束條件。針對此類問題，目前的求解方法主要是采用啟發式算法。粒子群算法具有搜索速度快，結構簡單等優點，但基本粒子群算法容易陷入局部最優的狀況，慣性權重ω是粒子群算法中的關鍵參數之一，它對粒子前進的速度有很好的控制作用，能顯著改善粒子優化狀況。采用了變ω的粒子群算法進行求解，慣性權重ω的表達式如下：

(14)

式中ωmax為最大慣性權重，本文中其值取作0.9；ωmin為最小慣性權重，文中取作0.4；Imax為最大迭代次數，文中取300；I為當前迭代次數。相較于傳統的固定ω的粒子群算法，變慣性權重ω的粒子群算法更易于使粒子趨向于全局搜索。

根據以上模型，具體算法流程如下：

(1)給定初始化條件，利用隨機生成函數將粒子初始化，每個粒子包含風電、火電和天然氣的輸入數據，限定粒子位置和速度的范圍；

(2)利用式(3)～式(6)，求取所有粒子的適應度值；

(3)由式(7)～式(13)，對全部粒子的可行性進行判斷，若滿足條件則保留該粒子，不滿足條件則采用罰函數的方式，將該粒子剔除；

(4)對所有的粒子，將其適應值分別與個體極值以及全局極值進行比較，得出最優的極值和最優位置；

(5)根據速度和位置更新公式，以及變慣性權重式(14)，更新每個粒子的速度和位置；

(6)判斷當前迭代次數是否已經達到最大迭代次數或所求的的全局最優位置否滿足最小界限，若滿足條件，則輸出最終結果，退出；若不滿足條件，則迭代次數加1，返回步驟(2)繼續執行。

算法流程圖如圖4所示。

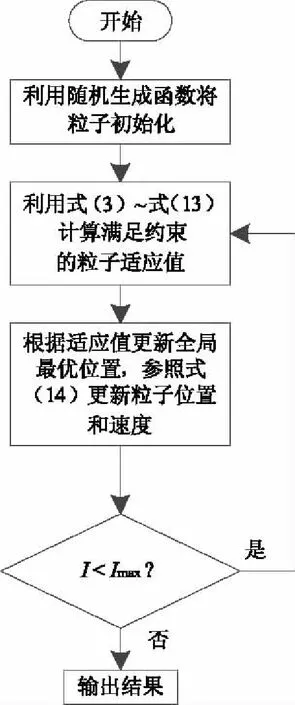
圖4 算法流程圖

3 算例分析

3.1 算例概況

本文參照文獻[4]中給出的基本參數為例進行分析，算例數據主要包括24 h電能、熱能需求、風電預測最大出力曲線以及實現聯供系統能源轉換設備參數。取天然氣的購買價格為3元/m3，天然氣的高熱值取10.8(kWh/m3)。上節提到的能源轉換設備的相應的轉換效率如表1所示。圖5為某日24 h電能和熱能負荷需求曲線，圖6所示為某日24 h最大可用風電出力曲線。

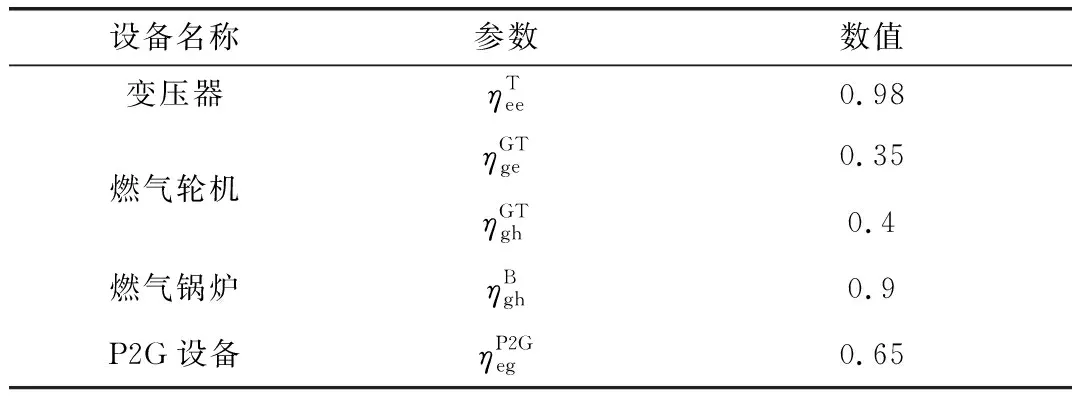
表1 設備轉換效率

為了分析驗證所提出的計及棄風成本下P2G設備對系統供能成本的影響，設計了以下3種測試場景：

場景1：考慮P2G設備使用，多余風電全部消納；

場景2：考慮P2G設備使用，多余風電部分消納；

場景3：不考慮P2G設備使用，多余風電全部不消納。

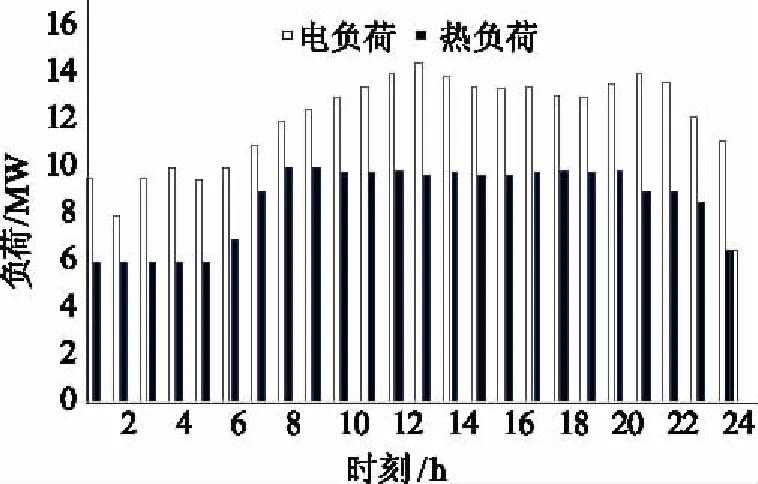
圖5 電能和熱能需求負荷曲線

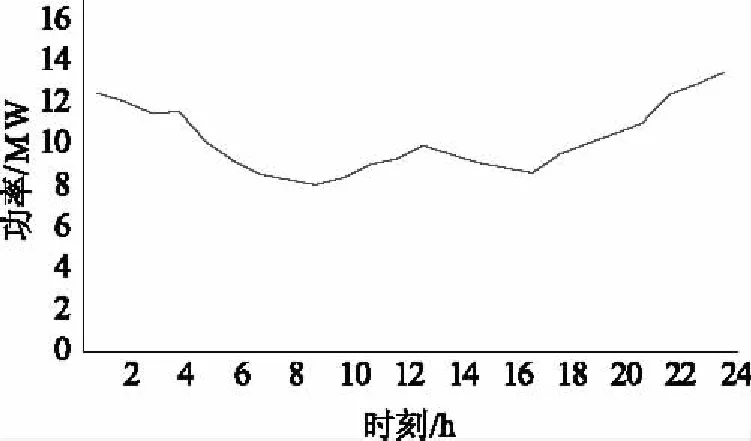
圖6 最大可用風電出力

3.2 算例結果

當考慮P2G設備存在且風電全部消納時，P2G消耗的功率以及燃氣輪機的出力如圖7所示。當1時～8時及18時～24時，由于風速相對較高，風機的輸出功率較大，而電負荷相對較小，此時，就會產生多余的風電。在此情況下，P2G設備啟動，消耗多余的風電，將其轉化為天然氣，供鍋爐燃燒供熱使用。而在8時～18時，由于風速相對較低，風機的輸出功率較小，而電負荷相對較大，此時，風電供能不足，啟動燃氣輪機，燃氣輪機通過消耗天然氣發出電能，補足電負荷的差額，在此情況下，燃氣輪機也發出熱能，供給所需的熱負荷需求。

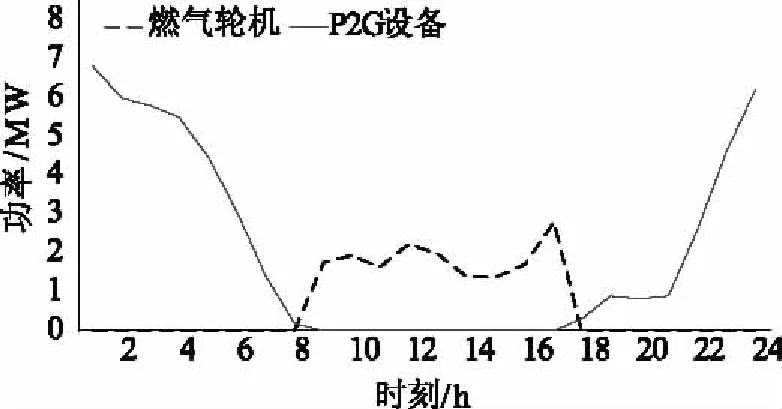
圖7 燃氣輪機和P2G設備出力曲線

圖8中所示為三種場景下，每小時的風電實際出力曲線圖。在1時～8時及18時～24時，風電出力過剩，三條曲線分別對應了三個場景下風電的實際出力，可以看出，與三個場景假設的情況相對應，場景3的實際出力最小，場景1的實際出力最大。而在9時～17時，風電完全被消納，不存在“棄風”問題，對應圖上就是三條曲線在該時間段重合。

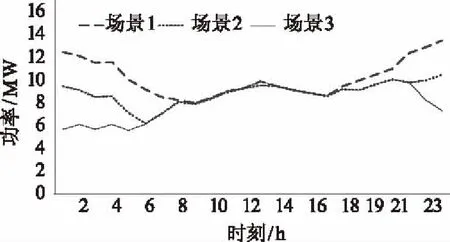
圖8 風電實際出力曲線

對三種場景下系統供能成本進行求解計算，計算結果如表2所示。

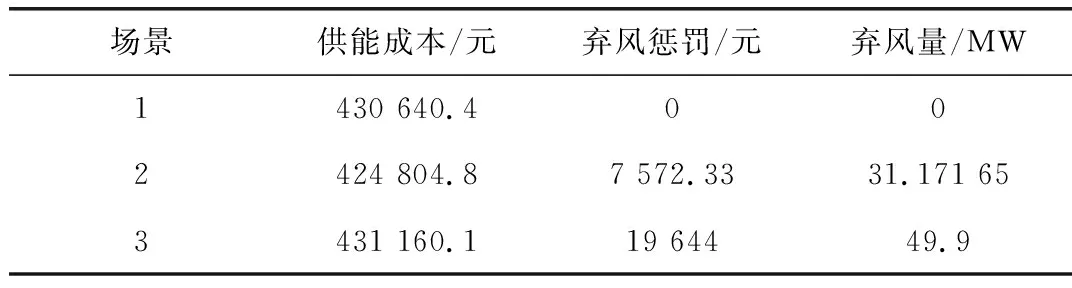
表2 結果比較

3種場景下，場景3的供能成本最大，主要原因是由于該場景情況下沒有考慮P2G設備的使用，此時多余的風電無法得到利用，產生大量的棄風，而由于棄風懲罰函數的懲罰因子是階梯形設置的，應用中棄風的量越大，棄風懲罰因子的數值也就取得越大，故，在這種情況下系統供能成本最大。而場景2的供能成本最小，此時相較于剩余風電全部消納情況，成本減少了5 835.6元，相較于剩余風電全部舍棄情況，成本減少了6 355.3元。這是由于，P2G設備可以將多余的風電轉化為天然氣，減少購氣側天然氣的購買量，相應的減少了購氣成本，但P2G設備的運行成本相對來說較高，當轉化的風電功率較少時，轉化風電帶來的收益不足以彌補P2G設備的運行成本，而且當計及棄風懲罰成本時，因為有大量的棄風，棄風懲罰成本會很大，該情況下系統總供能成本不會達到最少；而當P2G設備轉化的風電功率較大，乃至完全消納剩余風電，此時，雖然棄風懲罰成本很小，但是P2G設備的運行成本又會很大，系統總供能成本又會上升。所以根據懲罰因子分段函數的特性，只有當風電棄風量處于特定的范圍內時，此時的成本才是最低的，對應于文中就是當棄風量為31.171 65 MW時，系統供能成本是最低的，此時，相較于不使用P2G設備的情況，系統中的風電消納能力提升了7.67%。

4 結束語

提出了計及P2G設備運行成本和棄風成本的多能源系統模型，模型兼顧了系統運行的經濟性與風電消納能力。結果表明，引入P2G設備可以增強系統消納風電出力的能力，降低系統的運行成本。但目前P2G設備的單位運行成本相對高，當P2G設備轉化的功率較大時，運行成本反而會上升。后續工作中，將研究多能源系統中P2G設備運行對減少碳排放所帶來的經濟效益和環境效益。