連續梁拱組合結構風致抖振響應分析

余 海 洪

(中鐵四川生態城投資有限公司，四川 眉山 620500)

1 概述

連續梁拱組合結構是兩種形式的連續梁橋和拱組合。連續梁拱橋包含兩種結構的特征，具有結構剛度大，跨越能力強，動力性能好，外形美觀，施工方便等優點。近年來，這種類型的橋梁已經逐漸發展為超輕，大跨度，由風引起的抖振問題日益突出。

橋梁抖振是由湍流中的脈動組件引起的一種強迫振動。頻域分析方法是熱門的分析方法。本文選擇非線性時域分析方法，非線性時域分析方法能有效彌補頻域分析方法的不足。時域解的第一步是計算風荷載項的抖振力和自激力，并選擇準穩態氣動力學公式計算抖振力。我們使用Davenport的氣動導納函數來糾正它。然后用諧波綜合法模擬風場。本文基于35 m+130 m+35 m單肋連續梁拱組合橋的研究背景。利用數學軟件MATLAB和大型有限元軟件ANSYS進行數值模擬，研究了連續梁拱橋抖振的非線性行為。考慮結構的幾何非線性行為并與線性分析值進行比較。

2 橋梁有限元模型

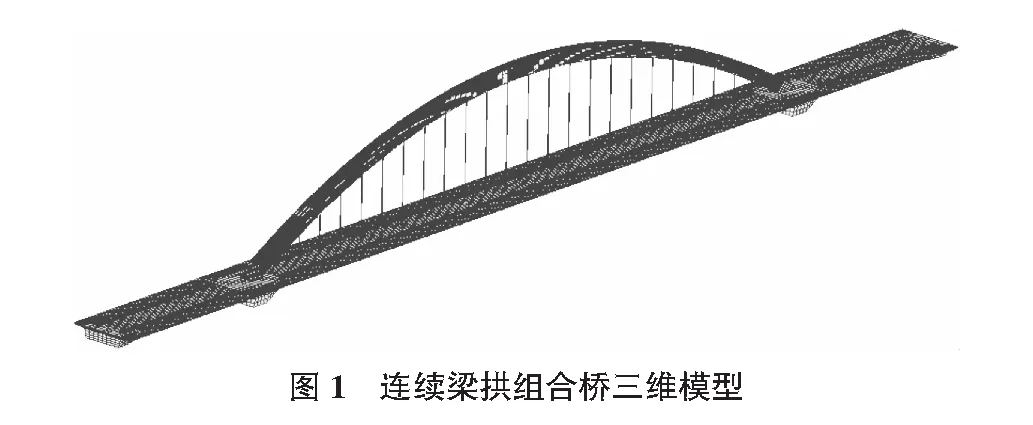
本文在35 m+130 m+35 m連續梁拱組合橋的基礎上進行研究，利用大型有限元軟件ANSYS建立了該橋的三維模型。梁單元選擇Beam188單元、吊桿選擇Link10單元，三維模型中X軸，Y軸，Z軸分別為橫橋向，梁高方向和順橋方向。材料特性如表1所示。圖1為全橋模型，對其進行動力計算，得到了橋梁的基本模態(見表2)。

表1 結構材料特性

如表2所示，此橋的基本頻率是0.745 Hz，周期是1.342 s，表示此橋整體剛度較大；基頻對應的振型為拱肋面外對稱側彎，主梁的橫向彎曲比較小，表示此橋主梁的橫向剛度比拱肋大；在前六階振型中拱肋發生扭轉，這表明拱肋的抗扭剛度比主梁的小；結構面內振動的基本頻率為2.579 Hz，面外振動基本頻率為0.745 Hz，面內振動基本頻率比面外基本頻率大，表示該橋在橫向穩定方面存在問題；此橋第一階扭轉出現在第2階振型，頻率為2.056 Hz，出現在面內振型之前，表明此橋梁的抵抗扭轉的剛度小于它的面內抗彎剛度。

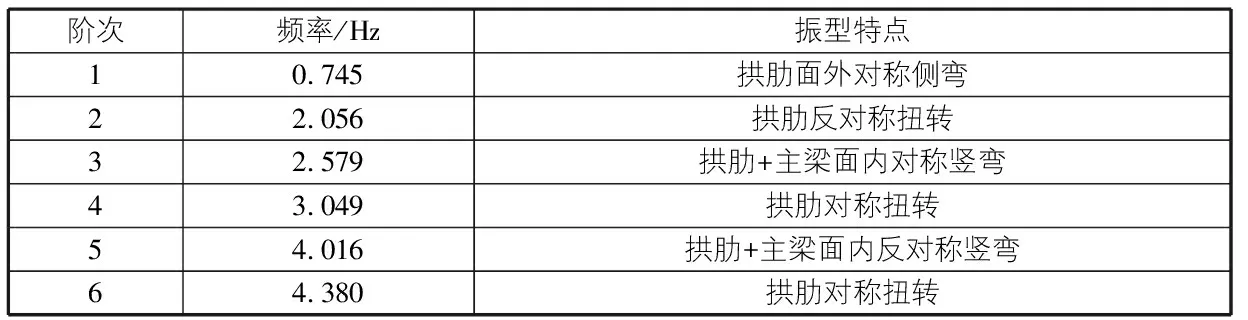
表2 前六階振型與頻率

3 結構風致響應分析

3.1 風場的模擬

選擇諧波合成法來模擬脈動風場的模數值，是一種運算不復雜、理論可靠、結果精度較高的方法。這種方法利用譜分解與三角余弦函數疊加以使數值接近的目的，這樣的方法可以較好的模擬隨機過程，跨度較大的連續梁拱組合橋的豎向尺寸與順橋向尺寸通常比橫橋向尺寸大的多，所以一般在利用諧波合成法來模擬脈動風場的時候，需要設置數量巨大的模擬點，這樣會導致計算很困難。所以我們通過不同結構的特點來簡化風場。依據本例的結構特點和振動基本模態，在模擬本組合橋的三維脈動風場時，可以將脈動風場簡化為主梁和拱肋沿橫橋向和垂直方向的維度為一維的線性隨機風速場。利用MATLAB軟件使用諧波合成法來模擬出隨機風速場。脈動風場在MATLAB中的基本參數如表3所示。主梁跨度為200 m，橋面高10 m，拱肋模擬點為跨中最高點即拱頂。脈動風場模擬基本參數如表3所示。

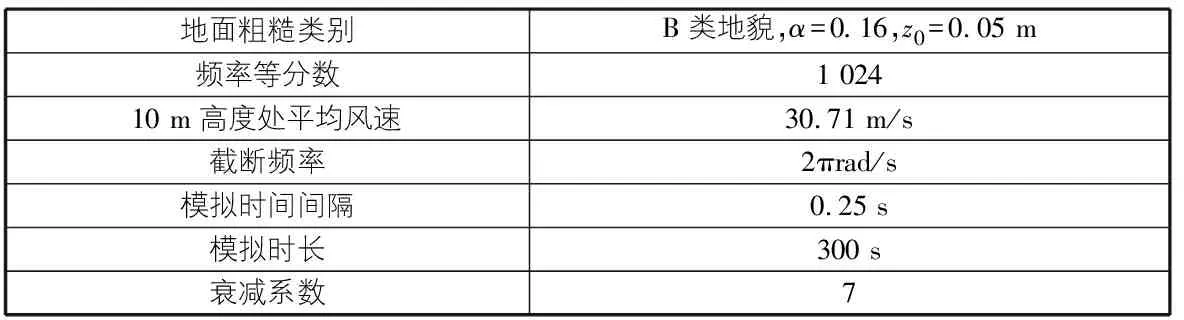
表3 脈動風場模擬基本參數

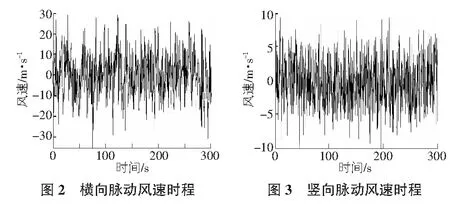
對MATLAB軟件模擬的脈動風場進行分析，該橋拱頂位置前300 s脈動風速時程片段如圖2,圖3所示，拱頂的水平和豎向脈動風速時程的平均值與0接近(<±0.5 m/s)，如圖2，圖3所示，脈動風場樣本的功率譜密度和目標譜函數的較為吻合，并且驗證它的紊流強度和相關數值等都在要求范圍之內，這表示該模擬風場符合要求，可以用來進行抖振力的計算和研究。

3.2 抖振力計算

在計算時根據Scanlan準定常氣動理論，氣動導納函數將被用來修正結果。此橋單位長度受到的荷載為：

(1)

(2)

(3)

其中，CD′(α),CL′(α),CM′(α)分別為阻力、升力和升力矩對攻角的導數；u(t),w(t)分別為水平和豎向的脈動風速。

加載的時候將抖振力時程加載在拱頂的節點上，并且考慮阻力、升力和扭矩的影響，抖振力時程用式(1)～式(3)進行運算可以算出，把運算得到的結果導入到ANSYS三維模型中，加載到關鍵節點然后進行分析，得到的模擬脈動風場時間步長和時間的步長一樣，一共取300 s，結構阻尼選取規范規定的阻尼比。本組合橋抖振響應運算數據如表4所示。表4中CD，CL，CM均為結構靜力三分力系數，CD′，CL′,CM′均為三分力系數對風攻角的導數。

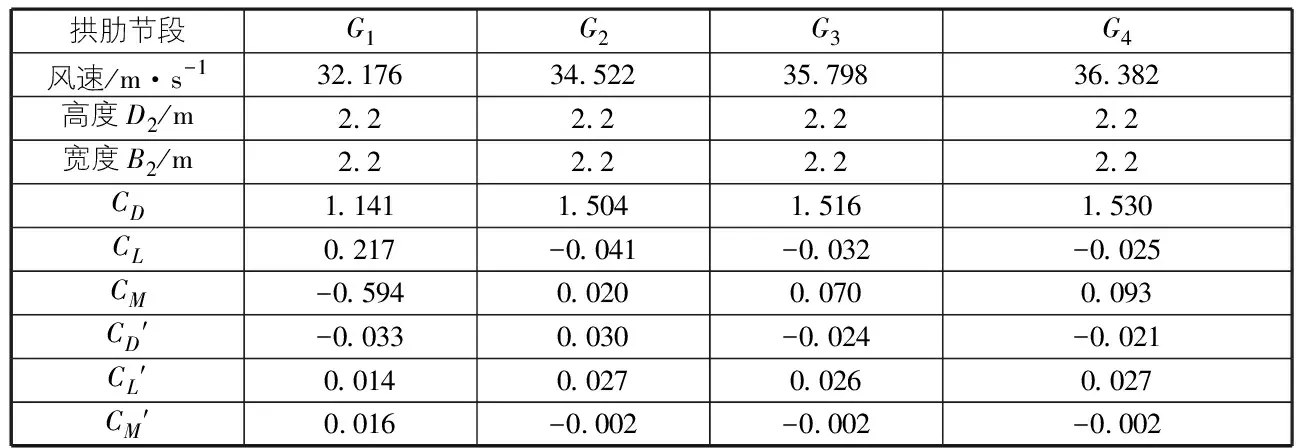
表4 拱頂抖振響應計算的基本參數

3.3 抖振響應分析對比

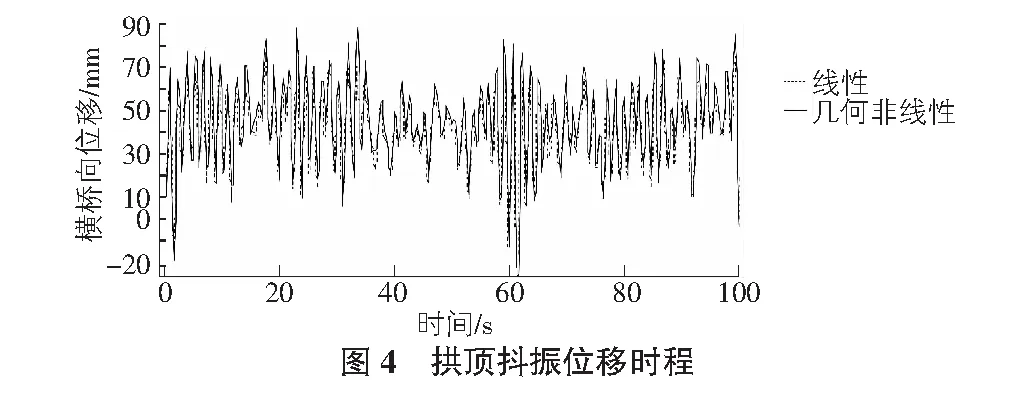
進行抖振時域運算分析，得到梁拱頂部關鍵部位的橫橋向位移與抖振扭轉位移時程曲線如圖4，圖5所示。

把該模型主要節點的位移時程結果利用均方根運算可以得出拱肋頂部的橫橋向、垂直方向還有抖振扭轉位移響應的數值，如圖6～圖8所示。

通過上面的數據可以得出，在抖振時域分析計算中，最大跨橋抖振位移峰值和最大抖振扭轉位移峰值出現在肋跨度上。 在非線性狀態后，拱肋在拱肋橫向上的抖動位移略大于線性情況下的拱形抖動位移，拱肋垂直抖振位移的RMS值減小。 拱肋擺動抖動傳遞RMS值比線性情況稍大，見表5。

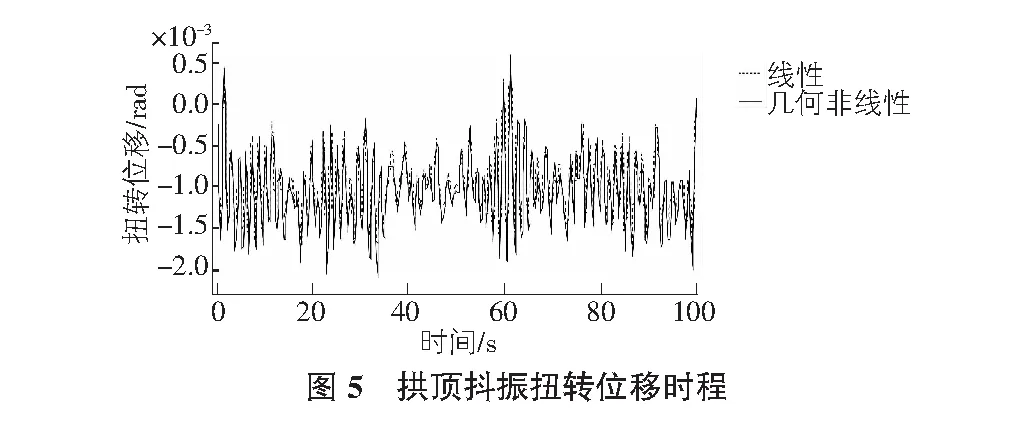
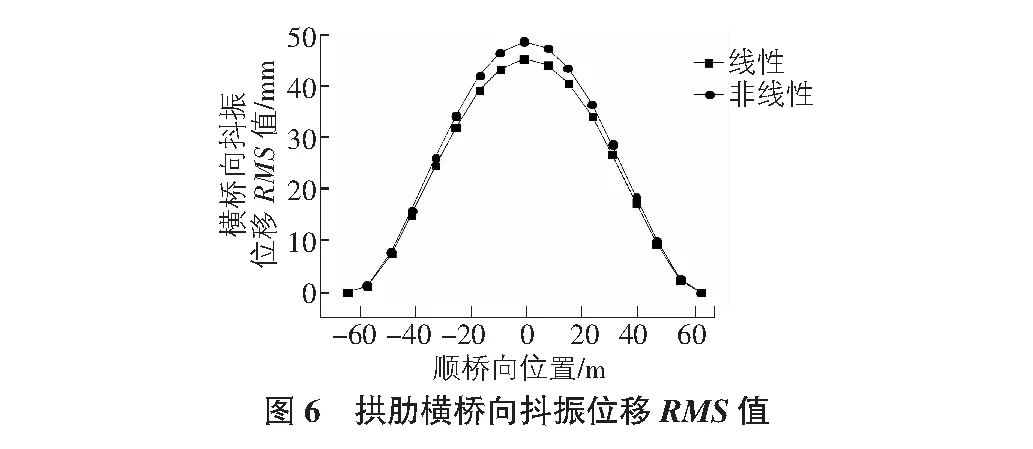
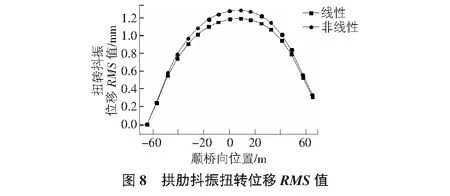
表5 主要截面位置的位移峰值(U=30.71 m/s)

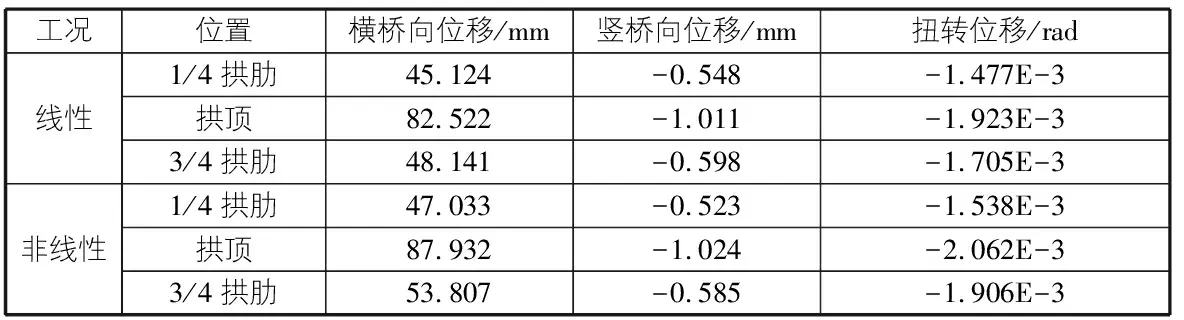
工況位置橫橋向位移/mm豎橋向位移/mm扭轉位移/rad線性非線性1/4拱肋45.124-0.548-1.477E-3拱頂82.522-1.011-1.923E-33/4拱肋48.141-0.598-1.705E-31/4拱肋47.033-0.523-1.538E-3拱頂87.932-1.024-2.062E-33/4拱肋53.807-0.585-1.906E-3

考慮到非線性情況，比較抖振內力響應的峰值，可以看出橋梁主要部分的軸力沒有明顯變化。右拱腳的垂直彎矩增加11%，右拱腳的力矩沿橋向增加12%，其余內力峰值幾乎沒有變化，見表6。

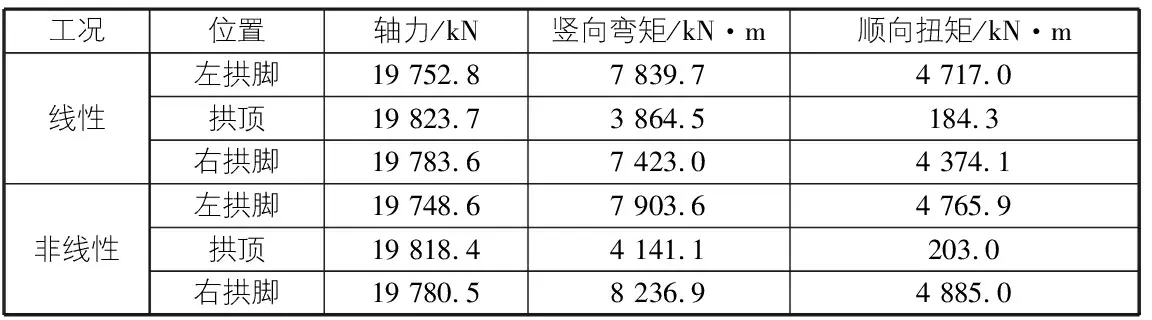
表6 主要截面位置的內力峰值(U=30.71 m/s)

4 結語

本文主要計算和分析連續梁拱組合橋的風致抖振響應。首先，進行脈動風場的數值模擬，然后將抖振力施加到橋上，并且優先進行抖振響應分析，得到了如下幾條結論：

1)在抖振時域分析計算中，最大跨橋抖振位移峰值和最大抖振扭轉位移峰值出現在肋跨度上。 在非線性狀態后，拱肋在拱肋橫向上的抖動位移略大于線性情況下的拱形抖動位移，拱肋垂直抖振位移的RMS值減小。 拱肋擺動抖動傳遞RMS值比線性情況稍大。

2)考慮到非線性，比較抖振內力響應的峰值，可以看出橋梁主要部分的軸力沒有明顯變化。右拱腳的垂直彎矩增加11%，右拱腳的力矩沿橋向增加12%，其余內力峰值幾乎沒有變化。

3)在設計風速范圍內，隨著風速的增加，交叉橋扭轉振動和拱肋扭轉振動的RMS值增大。垂直位移沒有明顯變化，表明風速對大跨度連續梁拱組合橋的橫向和扭轉位移有很大影響。 對豎向位移無明顯影響。