踐行“三學”，漸次生成“結構化板書”*
——以“分式單元起始課”教學為例

☉江蘇省海安市城南實驗中學劉東升

在當前幾種版本的初中數學教材中，分式都是獨立一章，主要學習分式的概念、基本性質、約分、通分、分式運算、分式方程及其應用等知識點，而這一章的第1課時通常只研究分式的定義、分式的意義問題、分式的值為0，教材內容十分簡單，有些教師就選擇了增加同類習題、大量訓練、變式拓展的方式來組織這節課的教學內容，使得本來簡單的教學內容變成枯燥、乏味的同類習題的反復操練.近年來，基于重組教材教學內容的單元教學得到很多老師的積極實踐［1］～［3］，“自學·議論·引導”教學提出“學材再建構”的操作要義［4］，得到積極的響應.本文接下來梳理分式單元起始課，就是基于“學材再建構”重組教學內容，并通過恰當追問、相機引導，體現“學法三結合”，追求“學程重生成”.

一、“分式單元起始課”教學活動與組織

活動（一）列方程解應用問題

問題1：把一些圖書分給某班學生閱讀，如果每人分3本，則剩余20本；如果每人分4本，則還缺25本.這批圖書有多少本？

問題2：一艘輪船在靜水中的最大航速為30千米/時，它沿江以最大航速順流航行90千米所用的時間，與以最大航速逆流航行60千米所用的時間相等，江水的流速為多少？

教學組織：安排學生獨立練習，5分鐘后交流展示，教師巡查過程中找出做得較快的學生把問題1和問題2所列的方程與方程的解寫到黑板“相應”位置上（注意，這里的相應位置很關鍵，因為后續教學進程中會有新增加的內容寫在黑板的其他位置，在本課小結階段將會形成漸次生成的結構化板書）.針對學生在問題2中設元、列式、找等量關系、列方程、解方程的過程進行追問，暴露他們的思維過程，待學生得到方程的解之后先對他們進行肯定，然后從他們解法的出發點開始分析，指出所列分式還沒有系統研究過，我們有必要先把分式的概念進行深入研究，才能保證后續學習有更穩固的基礎.這就引出下一個教學環節“從分數到分式”的教學活動.

活動（二）從分數到分式

研究內容：先研究分式的定義，然后借鑒分數的學習經驗展望分式研究的內容.

教學組織：先安排學生復習小學階段學習分數的內容，如果學生的回答比較零亂，教師可進行必要的干預，以便調整學生對分數學習順序的一些認知，在回顧了分數的學習內容之后，利用PPT呈現如下知識結構，如圖1.

圖1

然后讓學生對照上面的知識結構自主歸納分式的定義與展望學習內容.學生構建之后先在小組內交流、討論優化，最后大組展示對分式定義的理解，以及展望分式學習內容，教師在學生展示的同時，捕捉采集一些有效內容，漸次完善生成以下板書（分式學習的知識結構圖，如圖2）：

圖2

得出這個知識結構圖之后，告知學生教材上就是這樣的結構和順序，大家類比分數學習分式的探究很有價值.然后話鋒一轉，引導學生再回到分式的定義，指出對一個數學新概念的深刻理解是非常重要的，并安排學生交流對分式定義的理解.接下來，安排一組練習題，促進學生對分式定義、意義及分式的值為0的理解.

活動（三）深入研究分式定義

題1：列式表示下列各量：

（1）某村有n個人，耕地40公頃，人均耕地面積為______公頃.

（2）△ABC的面積為S，BC邊長為a，高AD為______.

（3）一輛汽車行駛a千米用b小時，它的平均車速為______千米/時；一列火車行駛a千米比這輛汽車少用1小時，它的平均車速為______千米/時.

教學組織：學生先練習，然后集中講評，先由學生匯報各自的解答，教師通過適時追問鞏固新知.比如，題1學生答對之后，追問學生：所列式子是分式嗎？理由是什么？題2學生答對之后，可追問：你們是根據什么來判定它們是分式的？理由是什么？對于題3，仍然要引導學生“回到定義”來解答；對于題4，有不少學生能做出答案，需要追問學生：你是如何理解的？特別是不但知道分子為0，更需要讓學生強化對分母不為0的理解.

活動（四）回顧小結

通過回顧本課內容，完善分式全章學習知識結構圖，對全章后續學習進行展望.

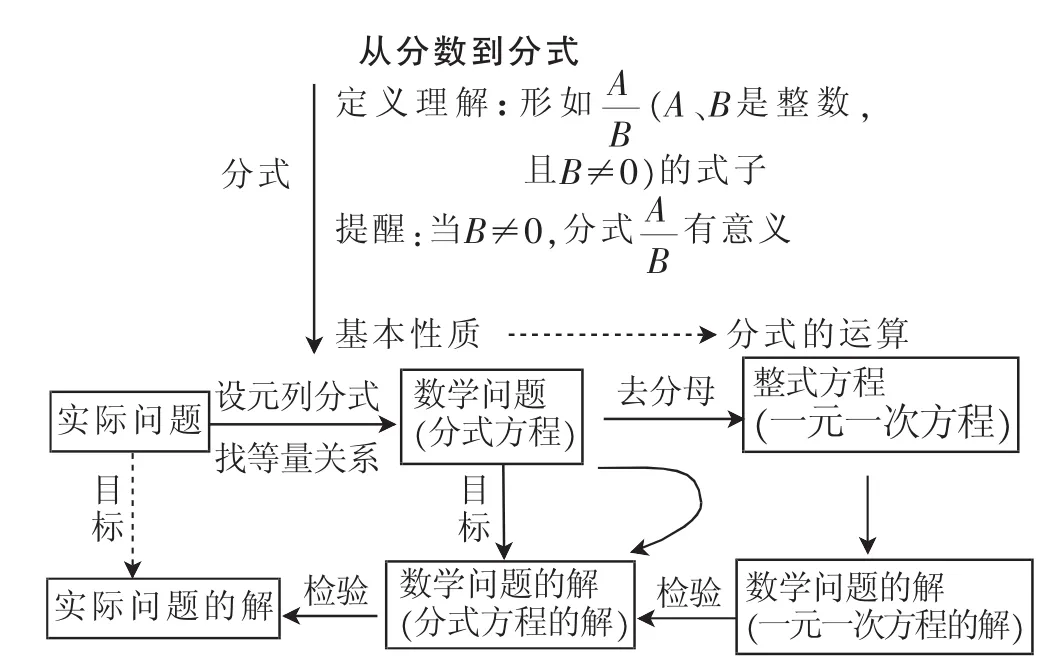
圖3

二、踐行“三學”，漸次生成“結構化板書”

1.踐行“學材再建構”，從“教教材”走向“用教材教”

“自學·議論·引導”倡導的“學材再建構”是基于對數學知識的深刻理解，認真研讀教材，但不拘泥于教材，更不能有教材是神圣不可侵犯的迷信、盲從思想.“大一統”的教材并不一定適合自己的校情、班情和學情，需要我們基于深刻理解［5］的高度重新構思教學內容的呈現順序、方式.以上文“分式單元起始課”來說，對于基礎較好的班情、學情來說，教材上分式第1節內容只安排了“從分數到分式”，學生根據小學時學習分數的經驗，都能實現自學達標，那么我們該如何將簡單的內容教深、教透呢？選擇從實際問題出發列出方程，驅動教學進程，引出分式的概念，并類比分數猜想、眺望分式的學習路徑.這樣既把教材第1節的內容進行了學習，避免了大量練習影響教學品質，又實現了從“教教材”走向“用教材教”的轉變.

2.加強“學法三結合”，學生獨立自學后再小組、大班展示

基于“學材再建構”設計的教案往往有很大的開放度，對教師駕馭課堂提出了更高的要求.因為這種教學設計拒絕“一個定義、三項注意、大量練習”模式，把用力點放在數學概念、數學定義等學習上，特別是在核心概念的教學上不惜時、不惜力.具體教學時，教師往往會從一個“引子”問題出發，安排學生獨立自學，然后小組內交流，再全班交流展示，教師適當進行評析，讓新知在合作學習中生成、生長、豐富起來.以分式單元起始教學為例，開課階段的兩個實際問題的求解應該先安排學生獨立練習（獨立自學），然后小組內交流，再選派幾個代表板書到黑板上，小組內可選派其他學生分工上臺講解他們求解的大致思路，以及解法的依據，這樣就有效融合了獨立自學、小組合作、全班展示，體現了“學法三結合”.

3.重視“學程重生成”，教師相機引導促進對話捕捉生成

“自學·議論·引導”的課堂倡導基 于預設的生成，這不是一種“密不透風”的“填空式”生成，而是某個問題驅動下的開放式生成，但學生生成的問題又能服務于教程和學程.在反比例函數起始課教學課例［6］中，我們以“反比例函數的圖像（雙曲線）是如何生成的”闡釋了學程重生成的操作要義.這里再以上文中“分式單元起始課”為例，在研究分式的概念之前，先安排學生回顧小學階段分數的學習經驗與路徑，然后安排學生交流并展望分式學習的內容，這樣就有了很多現場生成，但學生又不會“離題萬里”，教師相機引導與學生對話互動，教師要注意捕捉對話過程中有價值的信息，“采集”書寫到黑板相應位置，為課堂小結時完善成“結構化板書”做好準備.這里可順便提及“結構化板書”的特點，這種板書需要課前反復構思，調整不同內容在漸次生成過程中的位置，并充分預設課堂教學進程中捕捉到的內容，學生板演的位置等，以便在課堂小結時把這些內容進行梳理、結構化.甚至可以說，課前預設時想清“結構化板書”的內容“布置”與生成順序，這節課的備課其實就“成功”了一大半.

感謝：本課例在備課過程中得到著名特級教師李庾南老師的親自指導，課后成文的角度也得益于李老師的智慧點撥，謹致謝意！